【更多软件使用问题请点击亿道电子官方网站查询】
1、 文档目标
解决在programming algorithm界面中无法添加想要的Flash编程算法的问题
2、 问题场景
在对于Debug进行Flash Download进行配置的时候,在programming algorithm界面中有对应的Flash编程算法。可以通过下面的Add按键去添加Flash编程算法。但是在添加列表中没有想要的Flash编程算法。
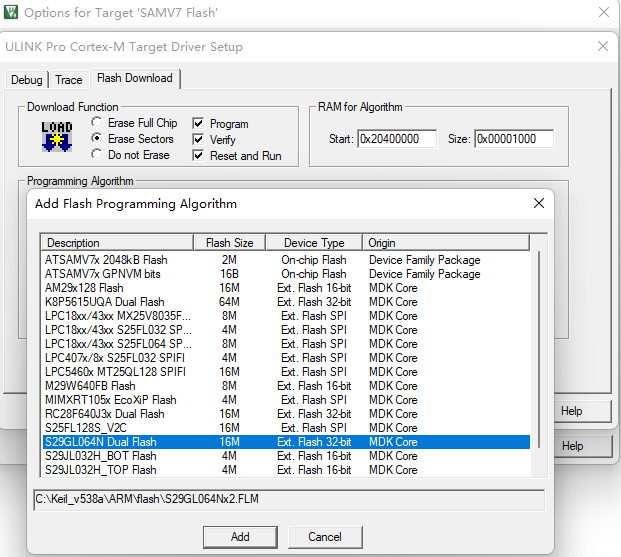
图 2-1
3、软硬件环境
1、软件版本:MDK 5.38a
2、电脑环境:Windows 11
3、外设硬件:无
4、解决方法
1、在图片2-1中所有的Flash算法都是由pack包(如图4-1)和软件自带的(图4-2)FLM文件导入的。
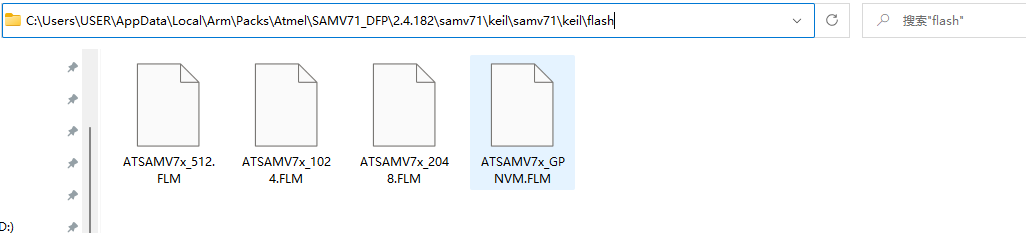
图4-1
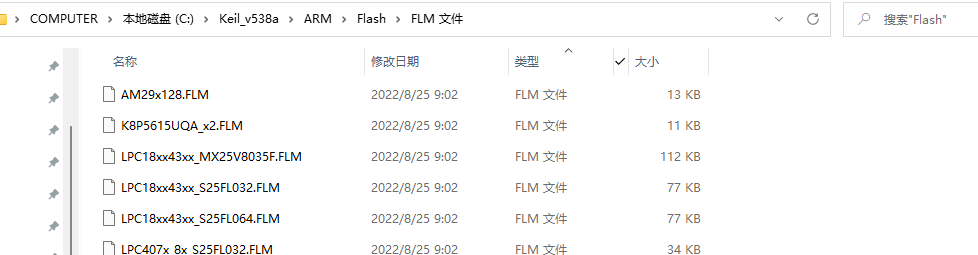
图4-2
2、那么如果想要在Add Flash Programming Algorithm窗口中添加想要的Flash编程算法,则可以通过将对应的FLM文件拷贝到MDK的安装目录下ARM\Flash文件夹中。然后,在Add Flash Programming Algorithm窗口中就会出现你拷贝到Flash文件夹下的Flash编程算法。再通过Add按钮就可以进行使用了。
————————————————————————
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
关于亿道电子
亿道电子技术有限公司(www.emdoor.cn)是国内资深的研发工具软件提供商,公司成立于2002年,面向中国广大的制造业客户提供研发、设计、管理过程中使用的各种软件开发工具,致力于帮助客户提高研发管理效率、缩短产品设计周期,提升产品可靠性。
二十多年来,先后与ARM、Altium、Ansys、QT、Green Hills、Minitab、EPLAN、QA Systems、OpenText、SureSoft、Visu-IT、PLS、Ashling、MSC Software、Autodesk、Source Insight、IncrediBuild、Lauterbach、Adobe、TestPlant等多家全球知名公司建立战略合作伙伴关系,并作为他们在中国区的主要分销合作伙伴服务了数千家中国本土客户,为客户提供从芯片级开发工具、EDA设计工具、软件编译以及测试工具、结构设计工具、仿真工具、电气设计工具、以及嵌入式GUI工具等等。亿道电子凭借多年的经验积累,真正的帮助客户实现了让研发更简单、更可靠、更高效的目标。