离散化算法，以Acwing802.区间和为例子（C++实现）

news2024/11/20 4:52:36

1.例题

假定有一个无限长的数轴，数轴上每个坐标上的数都是 0

现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加 c

接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r] 之间的所有数的和。

输入格式
第一行包含两个整数 n和 m


接下来 n 行，每行包含两个整数 x 和 c


再接下来 m 行，每行包含两个整数 l 和 r

输出格式共 m 行，每行输出一个询问中所求的区间内数字和。

数据范围
−10^9≤x≤10^9

1≤n,m≤10^5

−10^9≤l≤r≤10^9

−10000≤c≤10000

2.算法实现思路

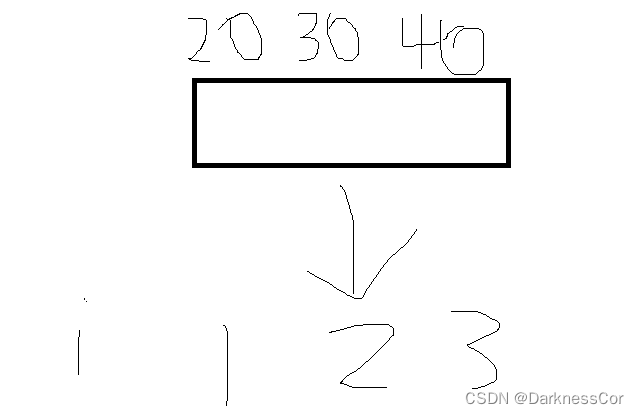
由于数轴是无限长的，所以我们无法直接使用前缀和算法来解题，但换种思路，该题的难点就在于由于数轴无限长所以限制了我们利用前缀和，所以我们可以换种思路，由于n和m都在10的五次方内，所以，此题给出的坐标数量最多不超过3*10的五次方个，我们就可以由这个数目将每个坐标进行映射，然后就可以使用前缀和来求解,离散化就是把大而分散的一段段使用到的稀疏区间，整合映射到连续的一段较小的稠密区间里，然后就可以通过普通前缀和公式来计算连续一段的区间和，本质上就是化大为小，把稀疏离散化简为稠密连续的一段。
在这里插入图片描述

3.代码

#include<bits/stdc++.h>
using namespace std;
const int N=3*1e5+10;
typedef pair<int,int>PII;
int a[N],s[N];
vector<PII>add,get1;
vector<int>alls;
int find(int x)
{
    int l=0,r=alls.size()-1;
    while(l<r)
    {   
        int mid=(l+r)/2;
        if(alls[mid]>=x)
        {
            r=mid;
        }
        else
        {
            l=mid+1;
        }
        
    }
    return l+1;
    
    
}
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++)
    {
        int x,c;
        cin>>x>>c;
        add.push_back({x,c});
        alls.push_back(x);
    }
    for(int i=0;i<m;i++)
    {
        int l,r;
        cin>>l>>r;
        get1.push_back({l,r});
        alls.push_back(l);
        alls.push_back(r);
    }
    sort(alls.begin(),alls.end());
    alls.erase(unique(alls.begin(),alls.end()),alls.end());
    for(auto item:add)
    {
        int x=find(item.first);
        a[x]+=item.second;
        
    }
    for(int i=1;i<=alls.size();i++)
    {
        s[i]=s[i-1]+a[i];
    }
    for(auto item:get1)
    {
     int l=find(item.first);
     int r=find(item.second);
     cout<<s[r]-s[l-1]<<endl;
    }
    return 0;
}