目标

在本实验中，你将:绘制逻辑回归模型的决策边界。这会让你更好地理解模型的预测。

import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from lab_utils_common import plot_data, sigmoid, draw_vthresh
plt.style.use('./deeplearning.mplstyle')

数据集

假设你有以下训练数据集

• 输入变量X是一个numpy数组，它有6个训练样本，每个样本有两个特征
• 输出变量y也是一个包含6个示例的numpy数组，y为0或1

X = np.array([[0.5, 1.5], [1,1], [1.5, 0.5], [3, 0.5], [2, 2], [1, 2.5]])
y = np.array([0, 0, 0, 1, 1, 1]).reshape(-1,1) 

图数据

让我们使用一个辅助函数来绘制这些数据。标签y = 1的数据点显示为红色,标记为y=0的数据点用蓝色圆圈表示。

fig,ax = plt.subplots(1,1,figsize=(4,4))
plot_data(X, y, ax)

ax.axis([0, 4, 0, 3.5])
ax.set_ylabel('$x_1$')
ax.set_xlabel('$x_0$')
plt.show()

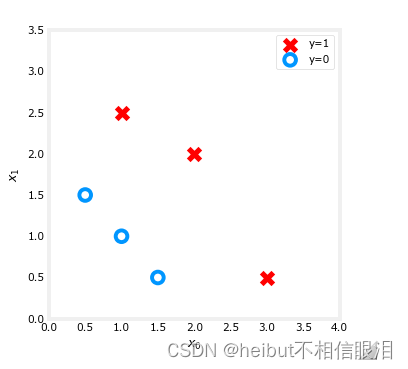
逻辑回归模型

• 假设您想在这个数据上训练一个逻辑回归模型，其形式为

F (x) = g(w0x0 + w1x1 + b)

g(z)是sigmoid函数

• 假设你训练了模型，得到的参数是b=-3, w0= 1 w 1=1。也就是说,

F (x) = g(xo +x1 - 3)

(您将在课程中学习如何进一步将这些参数拟合到数据中)让我们试着通过绘制决策边界来理解这个训练过的模型预测的是什么

复习逻辑回归和决策边界

• 回想一下，对于逻辑回归，模型表示为

fw.b (x^i) = g (w·x ^i + b)(1)

其中g(z)被称为sigmoid函数，它将所有输入值映射到0到1之间的值:

g (z) =1/(1+e^-z)

w·x是向量的点积

W·X= w0x0 + w1x1

• 我们将模型(fw.b(x))的输出解释为给定x并由w和b参数化的y= 1的概率。
• 因此，为了从逻辑回归模型中获得最终预测(y=0或y = 1)，我们可以使用以下启发式方法

如果fw,b(x) >= 0.5，则预测y=1
如果fw,b(x) < 0.5，则预测y = 0

• 让我们画出sigmoid函数，看看g(z) >= 0.5的地方

# Plot sigmoid(z) over a range of values from -10 to 10
z = np.arange(-10,11)

fig,ax = plt.subplots(1,1,figsize=(5,3))
# Plot z vs sigmoid(z)
ax.plot(z, sigmoid(z), c="b")

ax.set_title("Sigmoid function")
ax.set_ylabel('sigmoid(z)')
ax.set_xlabel('z')
draw_vthresh(ax,0)

• 如您所见，对于z>=0, g(z) >=0.5
• 对于逻辑回归模型，z = w·x+b。因此,

如果w·x+b>= 0，则模型预测y= 1
如果w·x+b<0，则模型预测y=0

绘图决策边界

现在，让我们回到我们的例子来理解逻辑回归模型是如何进行预测的。

• 我们的逻辑回归模型是这样的

f (x) = g ( -3 + x0 + x1)

• 从上面你学到的，你可以看到这个模型预测y= 1 如果-3+x0 +x1>=0

我们来看看它的图形是怎样的。我们先画出-3 +x0 +x 1= 0，也就是x1 =3- x0。

# Choose values between 0 and 6
x0 = np.arange(0,6)

x1 = 3 - x0
fig,ax = plt.subplots(1,1,figsize=(5,4))
# Plot the decision boundary
ax.plot(x0,x1, c="b")
ax.axis([0, 4, 0, 3.5])

# Fill the region below the line
ax.fill_between(x0,x1, alpha=0.2)

# Plot the original data
plot_data(X,y,ax)
ax.set_ylabel(r'$x_1$')
ax.set_xlabel(r'$x_0$')
plt.show()

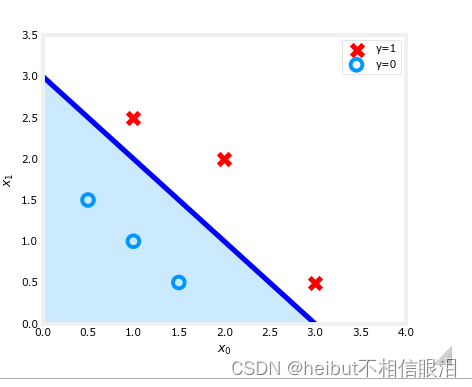
• 在上图中，蓝线表示x0 +x1-3=0，它应该与x1轴相交于3(如果我们设置x1 = 3, x0 =0)和x0轴相交于3(如果我们设置x1 =0, x0 = 3)。
• 阴影区域表示-3+x0+x1 <0。这条线上的区域是-3+xo+x >0。阴影区域(线下)的任何点都被分类为y =0。
• 直线上或直线上的任何点都归为y = 1。这条线被称为“决策边界”。

正如我们在讲座中看到的，通过使用高阶多项式项(例如:f(x)= g(x0^2 +x1-1))我们可以得到更复杂的非线性边界。

恭喜

你已经在逻辑回归的背景下探索了决策边界。