文章目录
- 目标
- 添加正则化
- 正则化代价函数
- 正则化梯度下降
- 重新运行过拟合示例
- 恭喜
目标
在本实验中,你将:
- 用正则化项扩展前面的线性和逻辑代价函数。
- 重新运行前面添加正则化项的过拟合示例。
import numpy as np
%matplotlib widget
import matplotlib.pyplot as plt
from plt_overfit import overfit_example, output
from lab_utils_common import sigmoid
np.set_printoptions(precision=8)
添加正则化


上面的幻灯片显示了线性回归和逻辑回归的成本和梯度函数。注意:
- 成本
- 线性回归和逻辑回归的成本函数有很大不同,但对方程进行正则化是相同的。
- 梯度
- 线性回归和逻辑回归的梯度函数非常相似。它们只是在实现Fwb方面有所不同
正则化代价函数
正则化线性回归的代价函数
代价函数正则化线性回归方程为:
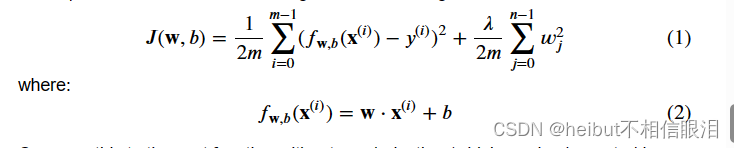
将此与没有正则化的成本函数(您在之前的实验室中实现)进行比较,其形式为:
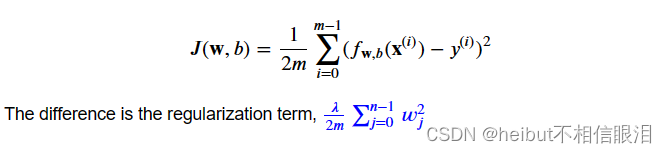
包括这一项激励梯度下降以最小化参数的大小。注意,在这个例子中,参数b没有被正则化。这是标准做法。下面是方程(1)和(2)的实现。注意,这使用了本课程的标准模式,对所有m个例子进行for循环。
def compute_cost_linear_reg(X, y, w, b, lambda_ = 1):
"""
Computes the cost over all examples
Args:
X (ndarray (m,n): Data, m examples with n features
y (ndarray (m,)): target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
lambda_ (scalar): Controls amount of regularization
Returns:
total_cost (scalar): cost
"""
m = X.shape[0]
n = len(w)
cost = 0.
for i in range(m):
f_wb_i = np.dot(X[i], w) + b #(n,)(n,)=scalar, see np.dot
cost = cost + (f_wb_i - y[i])**2 #scalar
cost = cost / (2 * m) #scalar
reg_cost = 0
for j in range(n):
reg_cost += (w[j]**2) #scalar
reg_cost = (lambda_/(2*m)) * reg_cost #scalar
total_cost = cost + reg_cost #scalar
return total_cost #scalar
运行下面的单元格,看看它是如何工作的。
np.random.seed(1)
X_tmp = np.random.rand(5,6)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1]).reshape(-1,)-0.5
b_tmp = 0.5
lambda_tmp = 0.7
cost_tmp = compute_cost_linear_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)
print("Regularized cost:", cost_tmp)
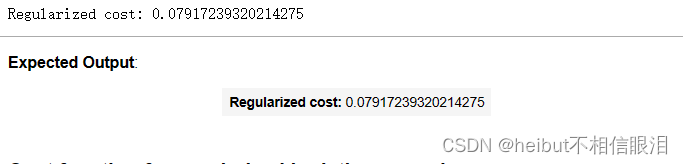
正则化逻辑回归的代价函数
对于正则化逻辑回归,成本函数为
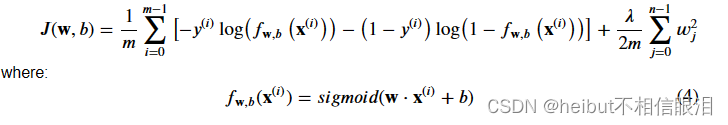
将此与没有正则化的成本函数(在之前的实验室中实现)进行比较: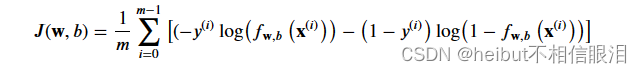
和上面的线性回归一样,区别在于正则化项,也就是

包括这一项激励梯度下降以最小化参数的大小。请注意。在这个例子中,参数b没有经过正则化。这是标准做法。
def compute_cost_logistic_reg(X, y, w, b, lambda_ = 1):
"""
Computes the cost over all examples
Args:
Args:
X (ndarray (m,n): Data, m examples with n features
y (ndarray (m,)): target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
lambda_ (scalar): Controls amount of regularization
Returns:
total_cost (scalar): cost
"""
m,n = X.shape
cost = 0.
for i in range(m):
z_i = np.dot(X[i], w) + b #(n,)(n,)=scalar, see np.dot
f_wb_i = sigmoid(z_i) #scalar
cost += -y[i]*np.log(f_wb_i) - (1-y[i])*np.log(1-f_wb_i) #scalar
cost = cost/m #scalar
reg_cost = 0
for j in range(n):
reg_cost += (w[j]**2) #scalar
reg_cost = (lambda_/(2*m)) * reg_cost #scalar
total_cost = cost + reg_cost #scalar
return total_cost #scalar
运行下面的单元格,看看它是如何工作的。
np.random.seed(1)
X_tmp = np.random.rand(5,6)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1]).reshape(-1,)-0.5
b_tmp = 0.5
lambda_tmp = 0.7
cost_tmp = compute_cost_logistic_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)
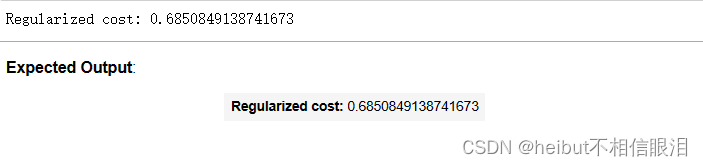
print("Regularized cost:", cost_tmp)
正则化梯度下降
运行梯度下降的基本算法不随正则化而改变,为:
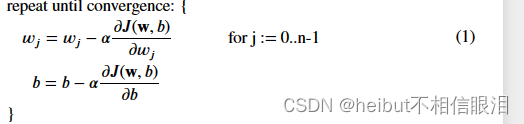
其中每次迭代对w执行同步更新。正则化改变的是计算梯度
用正则化计算梯度(线性/逻辑)
线性回归和逻辑回归的梯度计算几乎是相同的,不同的只是fwb的计算

正则化线性回归的梯度函数
def compute_gradient_linear_reg(X, y, w, b, lambda_):
"""
Computes the gradient for linear regression
Args:
X (ndarray (m,n): Data, m examples with n features
y (ndarray (m,)): target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
lambda_ (scalar): Controls amount of regularization
Returns:
dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w.
dj_db (scalar): The gradient of the cost w.r.t. the parameter b.
"""
m,n = X.shape #(number of examples, number of features)
dj_dw = np.zeros((n,))
dj_db = 0.
for i in range(m):
err = (np.dot(X[i], w) + b) - y[i]
for j in range(n):
dj_dw[j] = dj_dw[j] + err * X[i, j]
dj_db = dj_db + err
dj_dw = dj_dw / m
dj_db = dj_db / m
for j in range(n):
dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]
return dj_db, dj_dw
运行下面的单元格,看看它是如何工作的。
np.random.seed(1)
X_tmp = np.random.rand(5,3)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1])
b_tmp = 0.5
lambda_tmp = 0.7
dj_db_tmp, dj_dw_tmp = compute_gradient_linear_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)
print(f"dj_db: {dj_db_tmp}", )
print(f"Regularized dj_dw:\n {dj_dw_tmp.tolist()}", )

正则化逻辑回归的梯度函数
def compute_gradient_logistic_reg(X, y, w, b, lambda_):
"""
Computes the gradient for linear regression
Args:
X (ndarray (m,n): Data, m examples with n features
y (ndarray (m,)): target values
w (ndarray (n,)): model parameters
b (scalar) : model parameter
lambda_ (scalar): Controls amount of regularization
Returns
dj_dw (ndarray Shape (n,)): The gradient of the cost w.r.t. the parameters w.
dj_db (scalar) : The gradient of the cost w.r.t. the parameter b.
"""
m,n = X.shape
dj_dw = np.zeros((n,)) #(n,)
dj_db = 0.0 #scalar
for i in range(m):
f_wb_i = sigmoid(np.dot(X[i],w) + b) #(n,)(n,)=scalar
err_i = f_wb_i - y[i] #scalar
for j in range(n):
dj_dw[j] = dj_dw[j] + err_i * X[i,j] #scalar
dj_db = dj_db + err_i
dj_dw = dj_dw/m #(n,)
dj_db = dj_db/m #scalar
for j in range(n):
dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]
return dj_db, dj_dw
运行下面的单元格,看看它是如何工作的。
np.random.seed(1)
X_tmp = np.random.rand(5,3)
y_tmp = np.array([0,1,0,1,0])
w_tmp = np.random.rand(X_tmp.shape[1])
b_tmp = 0.5
lambda_tmp = 0.7
dj_db_tmp, dj_dw_tmp = compute_gradient_logistic_reg(X_tmp, y_tmp, w_tmp, b_tmp, lambda_tmp)
print(f"dj_db: {dj_db_tmp}", )
print(f"Regularized dj_dw:\n {dj_dw_tmp.tolist()}", )

重新运行过拟合示例
plt.close("all")
display(output)
ofit = overfit_example(True)
没拟合前如下所示(红色虚线是理想拟合曲线):
分类
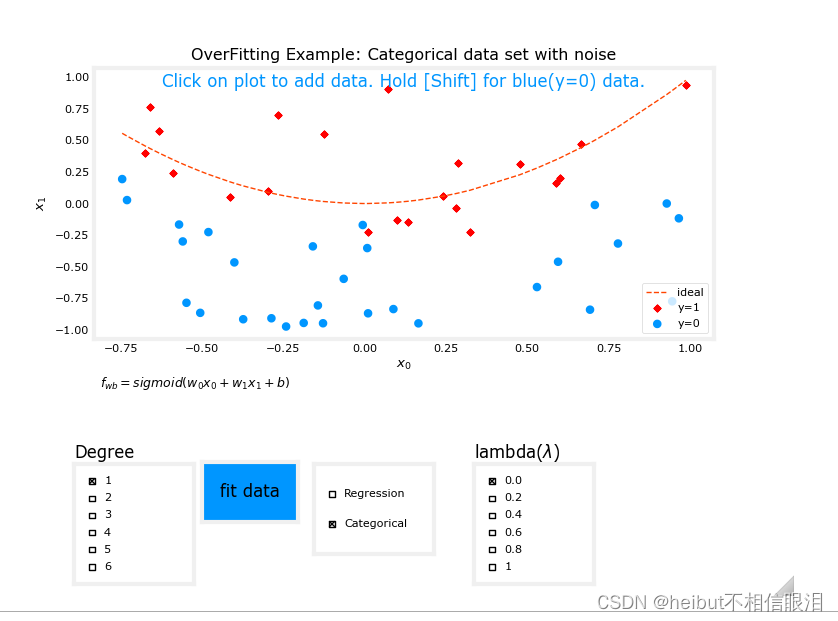
回归
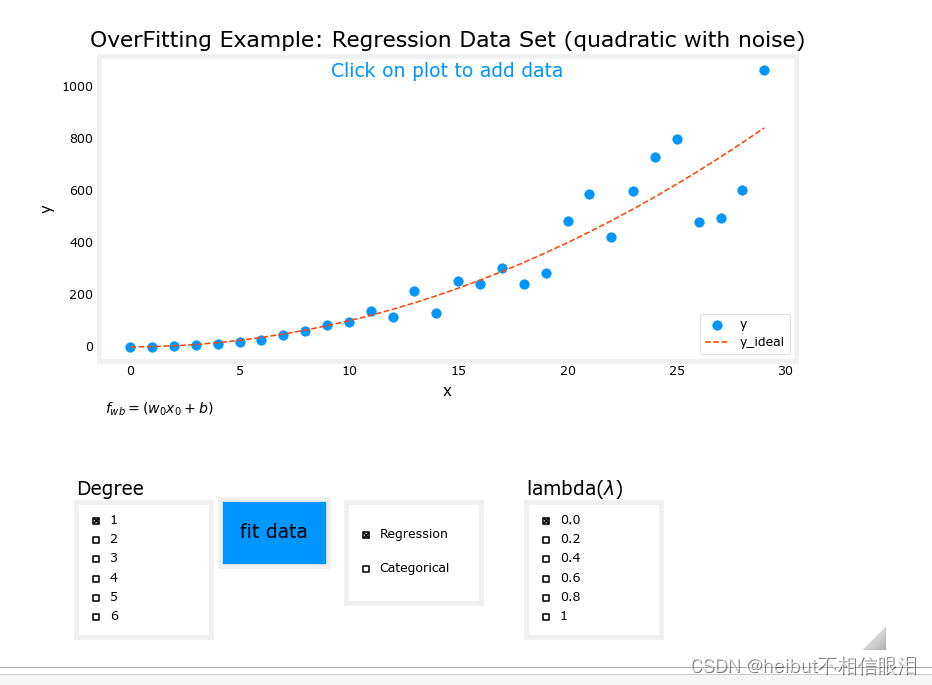
在上面的图表中,在前面的例子中尝试正则化。特别是:分类(逻辑回归)设置度为6,lambda为0(不正则化),拟合数据现在将lambda设置为1(增加正则化),拟合数据,注意差异。回归(线性回归)尝试同样的步骤。
分类
度为6,lambda为0(不正则化)如下: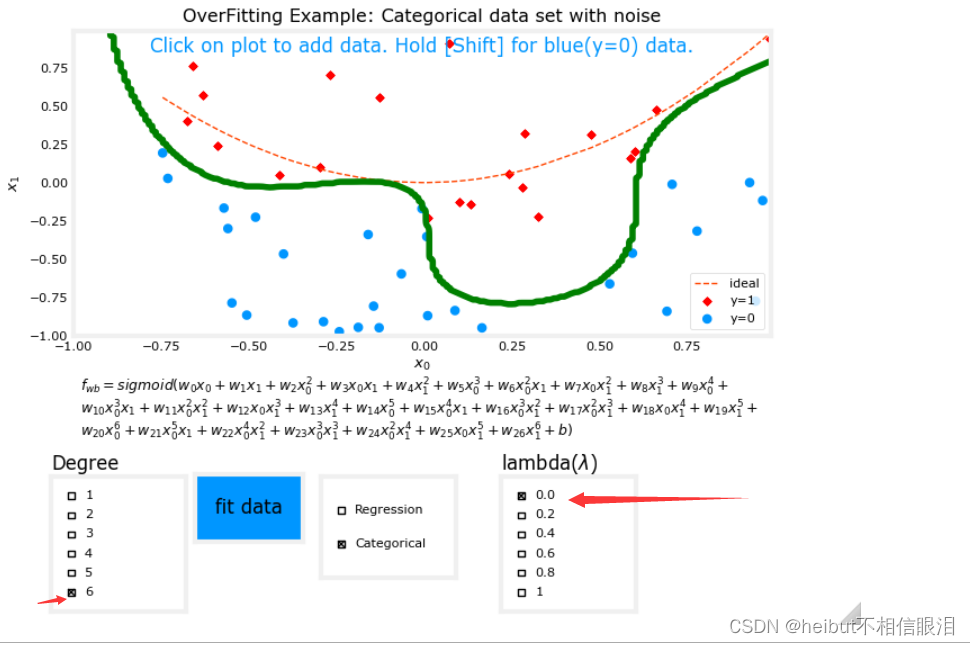
度为6,lambda为1(正则化)如下:
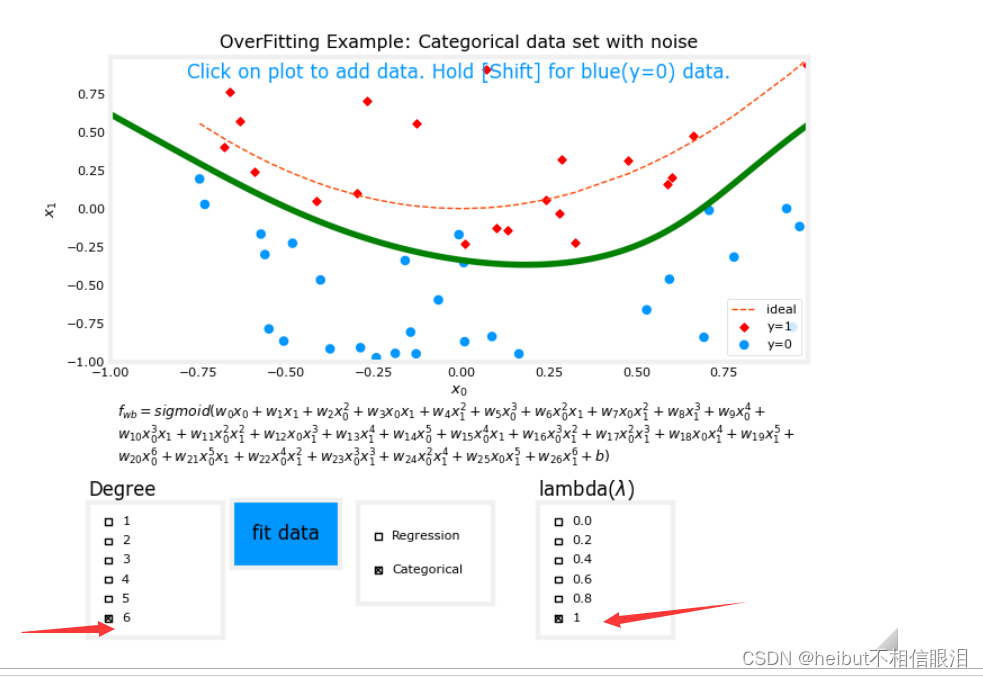
回归
度为6,lambda为0(不正则化)如下:
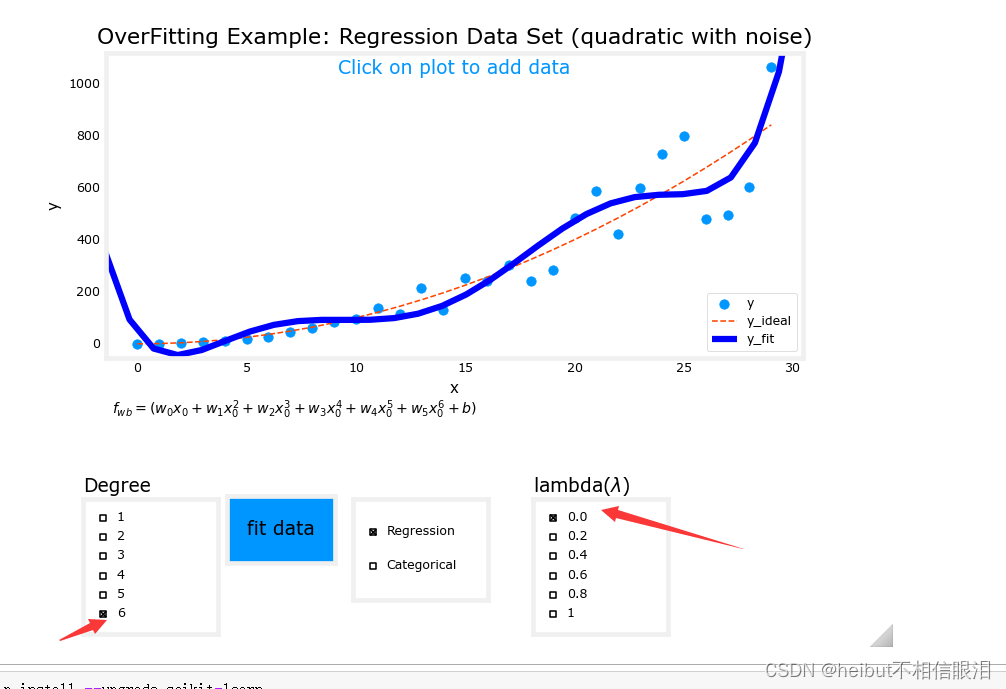
度为6,lambda为1(正则化)如下:
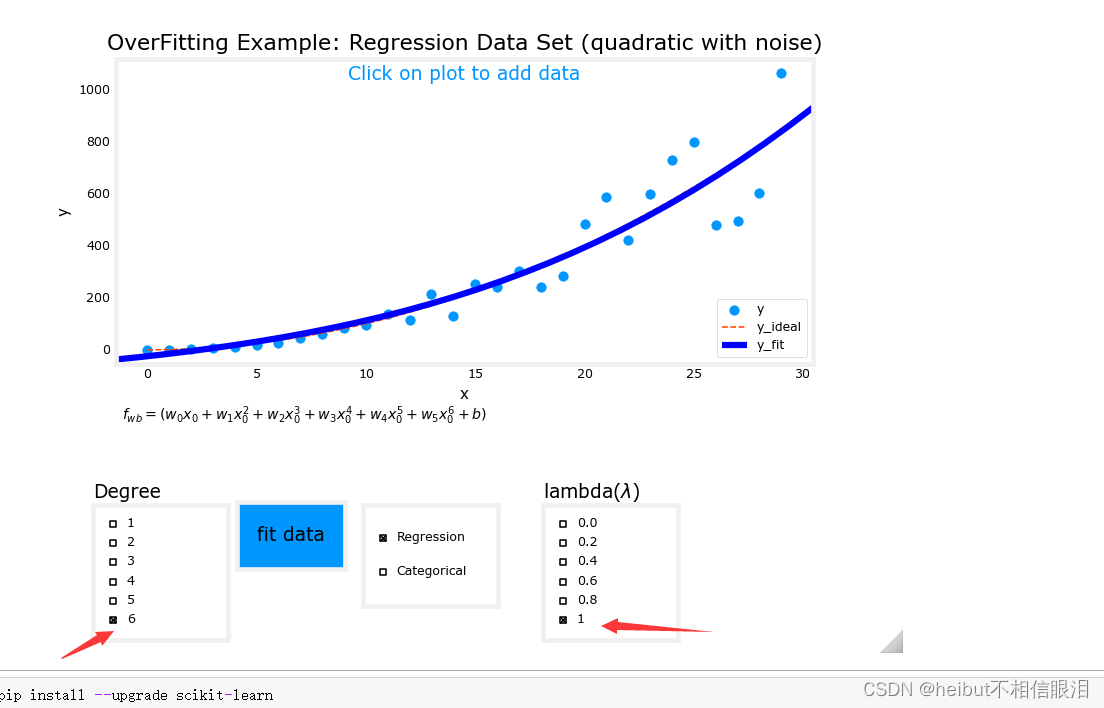
恭喜
你有:成本和梯度例程的例子与回归添加了线性和逻辑回归对正则化如何减少过度拟合产生了一些直觉