蜗牛 线性dp
目录
蜗牛 线性dp
先求到达竹竿底部的状态转移方程
求蜗牛到达第i根竹竿的传送门入口的最短时间编辑
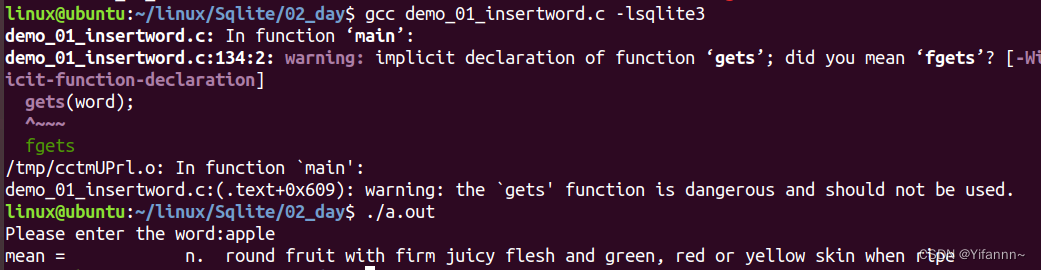
题目链接:蓝桥杯2023年第十四届省赛真题-蜗牛 - C语言网
关键在于建立数组将竹竿上的每个状态量表示出来,并分析出状态转移方程
int tree [] = new int[n];//记录每根竹竿到原点的距离
int portal_exit [] = new int[n];//第i个竹竿上传送门出口高度
int portal_entrance [] = new int[n];//第i个竹竿上传送门入口的高度
double time_bottom [] = new double[n];//到达第i个竹竿底部的最短时间
double time_portal [] = new double[n];//到达第i个竹竿传送门入口的最短时间注意:到达第i个竹竿传送门入口的最短时间也是,蜗牛传送到第i+1根竹竿传送门出口的最短时间
很明显,代码中表示最状态的数组为 time_bottom[i]表示蜗牛从原点到达第i根竹竿的底部用的最短时间
time_portal[i] 表示蜗牛从原点到达第i根竹竿可以传送到第i+1竹竿的传送门入口 a1的最短1时间
我们需要求出time_bottom[i]和time_poratal[i]的状态转移方程
先求到达竹竿底部的状态转移方程
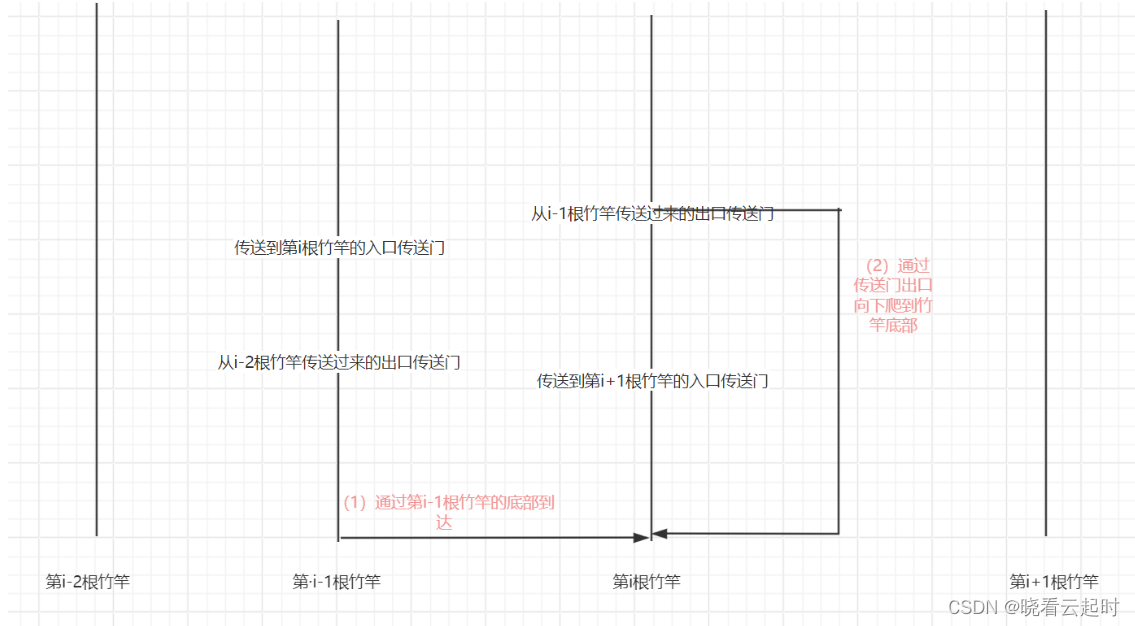
由图可知
到达第i竹竿底部的方法有两种
(1)从前一个竹竿的底部直接爬过来
time_bottom[i]=time_bottom[i-1]+tree[i]-tree[i-1];ps:tree[i]-tree[i-1]为蜗牛从前一个竹竿爬过来用的时间
(2)从当前竹竿的传送门出口爬下来
到达第i根竹竿底部的时间=蜗牛到达第i根竹竿的传送门出口的时间(即到达第i-1竹竿传送门入口的时间:time_portal[i-1])+ 传送门出口到底部距离/下爬速度
time_bottom[i]=time_portal[i-1]+portal_exit[i]/1.3;
综合(1)(2)得time_bottom[i]得状态转移方程
time_bottom[i]=Math.min(time_bottom[i-1]+tree[i]-tree[i-1],time_portal[i-1]+portal_exit[i]/1.3)求蜗牛到达第i根竹竿的传送门入口的最短时间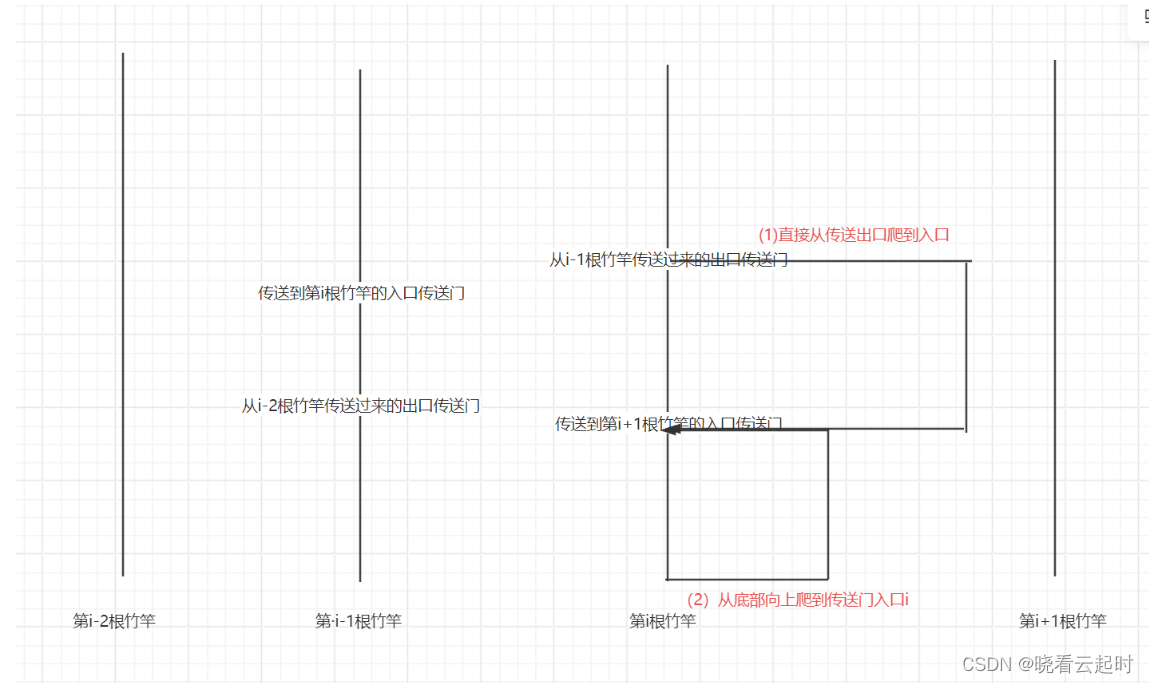
同样有两种方式
(1)从传送门出口爬到传送门入口
如果传送门出口比传送门入口高那么直接向下爬
到达传送门出口的时间+传送门出口-传送门入口的距离/速度
time_portal[i]=time_protal[i-1]+(portal_exit[i]-portal_entrance[i])/1.3;如果传送门出口的高度比入口的低那么就要向上1爬速度为0.7
(2)从底部爬到传送门
time_portal[i]=time_bottom[i]+portal_entrance[i]/0.7;综上time_portal[i]的状态转移方程为:(传送门出口比传送门入口高的情况)
ime_portal[i]=Math.min(time_protal[i-1]+(portal_exit[i]-portal_entrance[i])/1.3,time_bottom[i]+portal_entrance[i]/0.7)最后我们可以给第1根竹竿的状态初始化
//第一根竹竿的底部和传送出口最短时间我们可以算出来
time_bottom[0]=tree[0];//1
time_portal[0]=tree[0]+portal_entrance[0】;第n根竹竿我们要特殊判断一下因为最后一根竹竿没有传送门入口
完整代码
import java.util.Scanner;
public class Snail {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int tree [] = new int[n];//记录每根竹竿到原点的距离
int portal_exit [] = new int[n];//第i个竹竿上传送门出口高度
int portal_entrance [] = new int[n];//第i个竹竿上传送门入口的高度
double time_bottom [] = new double[n];//到达第i个竹竿底部的最短时间
double time_portal [] = new double[n];//到达第i个竹竿传送门入口的最短时间
for (int i=0;i<n;i++){
tree[i]=sc.nextInt();
}
for (int i=0;i<n-1;i++){
portal_entrance[i]=sc.nextInt();
portal_exit[i+1]=sc.nextInt();
}
//第一根竹竿的底部和传送出口最短时间我们可以算出来
time_bottom[0]=tree[0];//1
time_portal[0]=tree[0]+portal_entrance[0]/0.7;//2.4
for (int i=1;i<n;i++){
// 给出结束条件
if (i==n-1){
// 从上一根竹竿底部直接到第i根竹竿底部
double bottom1 = time_bottom[i-1]+tree[i]-tree[i-1];
// 从第i根竹竿的传送门出口向下爬到底部
double bottom2 = time_portal[i-1]+portal_exit[i]/1.3;
time_bottom[i]=Math.min(bottom1,bottom2);
break;
}else{
// 从上一根竹竿底部直接到第i根竹竿底部
double bottom1 = time_bottom[i-1]+tree[i]-tree[i-1];
// 从第i根竹竿的传送门出口向下爬到底部
double bottom2 = time_portal[i-1]+portal_exit[i]/1.3;//3.2
// 计算最短到达第i根竹竿底部的距离
time_bottom[i]=Math.min(bottom1,bottom2);//3.2
// 计算到达第i根竹竿传送门入口的最短时间
// 到达传送门入口的第一种方式:从底部爬到入口
double time_entrance1=time_bottom[i]+portal_entrance[i]/0.7;
// 到达传送门入口的第二种方式:从传送门的出口爬到入口
double time_entrance2=0;
if (portal_entrance[i]>=portal_exit[i]){//如果入口在出口上面,向上爬
time_entrance2=time_portal[i-1]+(portal_entrance[i]-portal_exit[i])/0.7;
}else {
time_entrance2=time_portal[i-1]+(portal_exit[i]-portal_entrance[i])/1.3;
}
// 从两种方式中取最短时间
time_portal[i]=Math.min(time_entrance1,time_entrance2);
}
}
System.out.printf("%.2f",time_bottom[n-1]);
}
}写下血与泪的教训:时间的数据类型一定要用double不然数据量太大精度不够不能通过。