【数据结构】顺序表的实现

文章目录

- **线性表(linear)：**
- **顺序表**
- - **下列是需要实现的接口(Seqlist.h)**
  - - **顺序表的初始化**
    - **顺序表的插入数据**
    - **顺序表的扩容(为插入数据提供保障)**
    - **顺序表的尾插**
    - **顺序表的头插**
    - **顺序表的删除数据**
    - **顺序表的尾删**
    - **顺序表的头删**
    - **查找指定位置的下标**
    - **顺序表的任意位置插入(pos是下标)**
    - **顺序表的判空**
    - **顺序表的打印**
    - **顺序表的销毁**

线性表(linear)：

线性表（linear list）:n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串…

线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储

顺序表

顺序表属于线性表的其中一种。顺序表在逻辑、物理结构上是连续。顺序表底层逻辑一般是数组。(物理结构上连续是指一段物理地址连续的存储单元依次存储数据元素的结构)

顺序表分为两种：静态顺序表和动态顺序表，每一种都属于它自己的价值，在实际中。一般使用动态顺序表做的，比如我们经常用的通讯录(因为静态顺序表只适合事前知道需要多少内存的情况下，不然会出现申请多少内存问题)

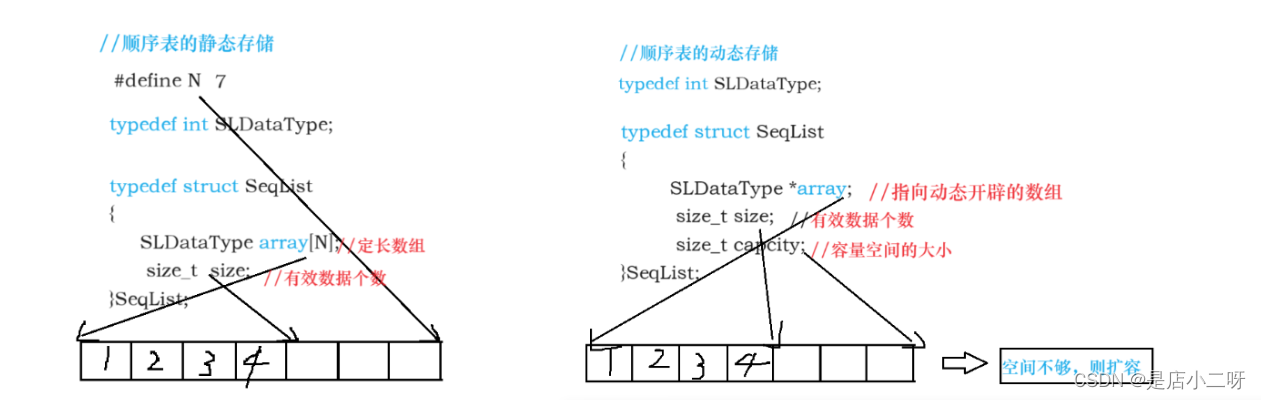
请添加图片描述

当我们有所了解顺序表的结构，接下来是实现顺序表的相关接口，比如增删查改

实现的过程中，创建两个源文件和一个头文件，分别为实现顺序表功能和测试顺序表功能，头文件一般用于声明函数(将在文章结尾处，贴出test.c文件)

注意:头文件只负责声明，在源文件中就是预编译阶段将多个头文件整合到一起

小技巧:

在循环中如果不知道结束条件的话，带入临界值去尝试是否符合条件
每一个接口都需要断言下传过来的指针是否为空指针->判断是否是一个有效的结构体变量

下列是需要实现的接口(Seqlist.h)

请添加图片描述

顺序表的初始化


void SLInit(SL* phead)
{
	assert(phead);
	phead->a = NULL;
	phead->size = phead->capacity = 0;
}

在实现该接口时:

这里空间上可以给数值

顺序表的插入数据

插入分为三类：头插尾插任意位置插入(其中任意位置插入，在实现查找功能先放着)
**前期准备:**在插入数据过程中，这里空间上可以给数值。当空间不足时，需向系统申请空间

顺序表的扩容(为插入数据提供保障)

void SLChekckCapacity(SL* phead)
{
	assert(phead);
	if (phead->size == phead->capacity)
	{
		int newcapacity =phead->capacity==0?4:phead->capacity * 2;
		SLDataType* pphead = (SLDataType*)realloc(phead->a, sizeof(SLDataType) * newcapacity);
		if (pphead == NULL)
		{
			perror("realloc fail!!");
			return 1;
		}
		phead->a = pphead;
		phead->capacity = newcapacity;
	}
}

在实现该接口时:

为存储数据而申请的一块空间，那么需要交给这个数据类型去维护
Capacity代表当前空间大小，Size代表当前有效数据，当有效数据充满了当前空间大小就需要申请内存空间（这里需要实现多次插入函数，这里单独实现SLChekckCapacity）
newcapacity是防止在扩容时，capacity为空(零乘任何数为零)，申请空间大小错误
最好不要phead直接接收扩容的地址，防止扩容(第二种情况)失败导致找不到之前空间地址
开辟以字符类型来维修开辟的空间，需要为‘\0‘开辟一个空间

顺序表的尾插

void SLPlusBack(SL*phead, SLDataType x)
{
	assert(phead);
    if(phead->size == phead->capacity)
	SLChekckCapacity(phead);
	phead->a[phead->size] = x;
	phead->size++;
}

在实现该接口时:

通过利用下标赋值

顺序表的头插

void SLPlusFront(SL* phead, SLDataType x)
{
	assert(phead);
    if(phead->size == phead->capacity)
	SLChekckCapacity(phead);
	for (int i = phead->size; i >0; i--)
	{
		phead->a[i] = phead->a[i - 1];
	}
	phead->a[0] = x;
	phead->size++;
}

在实现该接口时:

原数据整体向后移动，头会多出个数据将其覆盖，实现头插的效果
循环条件怎么设置，数据向后移动(覆盖并数值不丢失)，如果是从前先后覆盖，好比1 2 3 4 5 变成 1 1 2 3 4 5，将i的值赋值给i+1，i从首元素下标开始并且覆盖方式nums[i+1]=nums[i]

顺序表的删除数据

删除分为三类：头删尾删任意位置删除(其中任意位置删除，在实现查找功能先放着)
删除数据之前，要判断顺序表是否是为空–>这里有断言去判断

顺序表的尾删

void SLPopBack(SL* phead)
{
	assert(phead);
	assert(phead->a);
	phead->size--;
}

在实现该接口时:

不是将数据设为0就是删除数据。正确的做法，通过size（有效数据个数）个数控制
顺序表不访问size外的无效数据，那么从某种意义上是删除了数据（班里有位同学退学，班里人数少一位，同学还是存在，只是座位没有它）
空间是不浪费的，尾插数据时，可能下次还是用到那个空间

顺序表的头删

void SLPopFront(SL* phead)
{
	assert(phead);
	assert(phead->a);
	for (int i = 0; i < phead->size-1; i++)
	{
		phead->a[i] = phead->a[i + 1];
	}
	phead->size--;
}

在实现该接口时:

数组删除数据的方式就是覆盖数据，那么只需要从后向前覆盖，首元素将被覆盖或者被删除
循环条件怎么设置，如果是从后先前覆盖，好比1 2 3 4 5变成 2 3 4 5 5，将i+1的值赋值给i，i从首元素下标开始并且覆盖方式nums[i]=nums[i+1];

查找指定位置的下标

为了实现对某个位置进行修改，需要利用到顺序表中查找接口

int SLFind(SL* phead, SLDataType x)
{
	assert(phead);
	assert(phead->a);
	for (int i = 0; i < phead->size; i++)
	{
		if (phead->a[i] == x)
            return i;
	}
	return -1;
}

在实现该接口时:

遍历顺序表，如果满足条件返回当前位置的下标，没有找到返回一个负数表示找不到
开始实现任意位置上的修改(任意是相对的，需要对pos进行限制)
顺序表的任意位置插入(pos是下标)

void SLInsert(SL* phead, int pos, SLDataType x)
{
	assert(phead);

	assert(0 <= pos && pos <= phead->size);
		SLChekckCapacity(phead);
		for (int i = phead->size; i>pos;i--)
		{
			phead->a[i] = phead->a[i-1];//pos+1 pos-->注意覆盖的顺序,向后就是后面开始
		}
		phead->a[pos] = x;	
		phead->size++;
}

在实现该接口时:

需要对pos设置范围
以下标pos为界，pos之后的数据向后移动（跟头插类似，主要是在循环条件略显差异）
不要忘记上面的小技巧，任何得到正确的循环条件

顺序表的任意位置插入(pos是下标)

void SLErase(SL* phead, int pos)
{
	assert(phead);
	assert(pos >= 0 && pos < phead->size);
	for (int i = pos;i<phead->size-1;i++)
	{
		phead->a[i] = phead->a[i + 1];
	}
	phead->size--;
}

在实现该接口时:

需要对pos设置范围
以下标pos为界，pos之后的数据向前移动(跟头删是类似的，主要是在循环条件略显差异)

顺序表实现任意位置插入、插入跟头尾插删是类型的。但是上面的操作相当于基础，也是需要学习的(只有学会1+1，才能学会7+8)

顺序表的判空

bool SLEmpty(SL*phead)
{
	assert(phead);
    assert(phead->a);
    return phead->size==0;
}

顺序表的打印

void SLPrintData(SL*phead)
{
	assert(phead);
	for (int i = 0; i < phead->size; i++)
	{
		printf("%d ", phead->a[i]);
	}
	printf("\n");
}

顺序表的销毁

void SLDestory(SL*phead)
{
	assert(phead);
	if (phead->a)
	{
		free(phead->a);//free该前顺序表的动态开辟的空间
		phead->a = NULL;
		phead->size = phead->capacity = 0;
	}	
}

补充:贴出test.c文件

test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "Seqlist.h"

void test4()
{
	SL phead;
	SLInit(&phead);
	SLPlusBack(&phead, 3);
	SLPlusBack(&phead, 4);
	SLPlusBack(&phead, 5);
	SLPrintData(&phead);
	SLInsert(&phead,1, 100);//这个pos是下标，pos之后插入
	SLPrintData(&phead);
	SLErase(&phead,1);
	SLPrintData(&phead);
	int pos = SLFind(&phead, 3);//可以找到当前下标
//实现定位
	SLDestory(&phead);
}
int main()
{
	test4();
	return 0;
}