---

题目描述

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

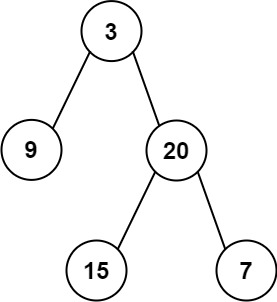
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]
示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

解题思路

我感觉这道题的注释不是很好写的很清晰，建议先看一下另外一道题的思路：最大二叉树
然后回来再看这道题的注释就会清晰很多

代码

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return build(inorder,0, inorder.length-1,postorder,0, postorder.length-1);
    }

    //这个函数负责构造二叉树
    public TreeNode build(int[] inorder,int leftIndex,int rightIndex,int[] postorder,int postLeftIndex,int postRightIndex){

        //如果left坐标小于right坐标，则表明是一个空树，也是递归出口
        if (leftIndex>rightIndex||postLeftIndex>postRightIndex){
            return null;
        }
        //构造根节点
        TreeNode root  = new TreeNode(postorder[postRightIndex]);
        //找到根节点在中序遍历中的位置
        int rootIndex = 0;
        for (int i = leftIndex; i <= rightIndex; i++) {
            if (inorder[i]==root.val){
                rootIndex=i;
                break;
            }
        }
        //中序遍历中rootIndex-leftIndex表示左子树有多少个节点
        int lenOfLeft = rootIndex-leftIndex;
        //寻找左子树的根节点,最后一个参数表示左子树的后序遍历序列结束的位置
        TreeNode leftChild = build(inorder,leftIndex,rootIndex-1,postorder,postLeftIndex,postLeftIndex+lenOfLeft-1);
        //寻找右子树的根节点
        TreeNode rightChild = build(inorder,rootIndex+1,rightIndex,postorder,postLeftIndex+lenOfLeft,postRightIndex-1);
        //root分别指向左子树和右子树
        root.left = leftChild;
        root.right = rightChild;
        return root;
    }
}