题目：

恰逢 H 国国庆，国王邀请 n 位大臣来玩一个有奖游戏。
首先，他让每个大臣在左、右手上面分别写下一个整数，国王自己也在左、右手上各写一个整数。
然后，让这 n 位大臣排成一排，国王站在队伍的最前面。
排好队后，所有的大臣都会获得国王奖赏的若干金币，每位大臣获得的金币数分别是:
排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏，所以他想请你帮他重新安排一下队伍的顺序，使得获得奖赏最多的大臣，所获奖赏尽可能的少。
注意，国王的位置始终在队伍的最前面。

思路：

我们先从两个大臣开始。

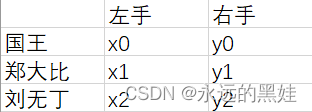
 此时我们的答案是：answer1=max(x0/y1,x0*x1/y2);

我们调换大臣的顺序。

 我们的第二个答案是：answer2=max(x0/y2,x0*x2/y1);

我们要从answer1和answer2中找出最大的。我们对比答案发现x0*x1/y2>x0/y2和x0*x2/y1>x0/y1;

所以我们只需比较x0*x1/y2和x0*x2/y1。

如下图

 

 

 所以我们以两个为例我们最后得出我们只需比较x1*y1与x2*y2的值即可。我们在已多个大臣为例。我们令前n-2位大臣的左手累乘为R。我们看第n-1位和第n位这两个大臣。

如图

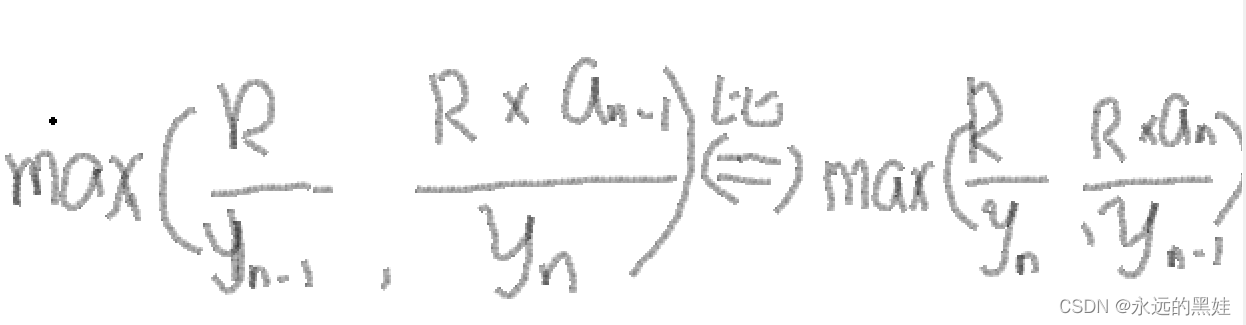
 我们最后得出我们要看的相互比较的值为

如图

 到这里我们发现了我们要比较的值应该是an-1*bn-1与an*bn这两个值的大小，我们从小推大，如果是两个大臣我们比较将a1*b1与a2*b2进行比较选出最大的将其放到放到后面这样我们就可以保证最后一个大臣获得的赏金是最符合条件的。

同理三个大臣也是这种方法，三个以上的大臣也一样，多少大臣也一样。将an*bn大的尽量往后面放即可，最后将前面大臣的左手的值累乘，再÷最后一位大臣的右手值。即可。不要忘了采取高精度乘除法。

#include<bits/stdc++.h>
using namespace std;
int s[1000000]={1},ans[1000000],slen=1;
struct people
{
	int a,b;
}num[10005];
bool cmp(people p1,people p2)
{
	return  p1.a*p1.b<p2.a*p2.b;
}
void chen(int n)
{
	int tem=0;
	for(int i=0;i<slen;i++)s[i]*=n;
	for(int i=0;i<slen;i++)
	{
	 tem+=s[i];
	 s[i]=tem%10;
	 tem/=10;
	}
	while(tem!=0)
	{
	  s[slen]=tem%10;
	  slen++;
	  tem/=10;
	}

}
void chu(int n)
{
	int tem=0;
	for(int i=slen-1;i>=0;i--)
	{
	 tem=tem*10+s[i];
	 ans[i]=tem/n;
	 tem%=n;
	}
}
void print()
{
	int tem=slen;
	while(ans[tem]==0)
	{
	    tem--;
	    if(tem==-1)
	    {
	    	   cout<<1;
	    	   return ;
	    }
	}
	for(int i=tem;i>=0;i--)
	{
	   	   cout<<ans[i];
	}
}
int main()
{
   int nums;cin>>nums;
   for(int i=0;i<=nums;i++)cin>>num[i].a>>num[i].b;
   sort(num+1,num+nums+1,cmp);
   for(int i=0;i<nums;i++)
   {
   	chen(num[i].a);
   }
   chu(num[nums].b);
   print();
}