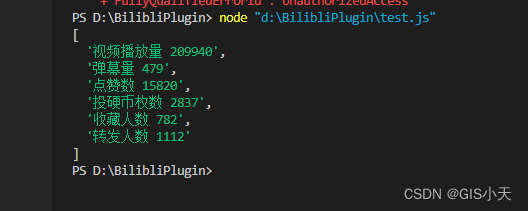
题目
儿童节那天有 K 位小朋友到小明家做客。
小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N 块巧克力,其中第 i 块是 Hi×Wi 的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。
切出的巧克力需要满足:
- 形状是正方形,边长是整数
- 大小相同
例如一块 6×5 的巧克力可以切出 6 块 2×2 的巧克力或者 2 块 3×3 的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小明计算出最大的边长是多少么?
输入格式
第一行包含两个整数 N 和 K。
以下 N 行每行包含两个整数 Hi 和 Wi。
输入保证每位小朋友至少能获得一块 1×1 的巧克力。
输出格式
输出切出的正方形巧克力最大可能的边长。
数据范围
1≤N,K≤10^5,
1≤Hi,Wi≤10^5输入样例:
2 10 6 5 5 6输出样例:
2
思路:
第一个问题,每块巧克力最大可以分成边长为多少的正方形?
假设巧克力的大小为 。
那么每个巧克力最大可以被分为 或者
大小。
一个 大小的巧克力最多可以被分成多少个
大小的巧克力?
块,行数除以
向下取整 则是能在行上最多能分到的最多的块数,同理列,那么在行数上能分得的最多块数 * 列上能分得的最多块数就是一块巧克力能被分得的最多的块数。
因此,我们只需要取所有巧克力中长度的最大值max,从1枚举到max,就可以找出能够分得的最大块数。(使用二分代替枚举 O(n)->O(logn))
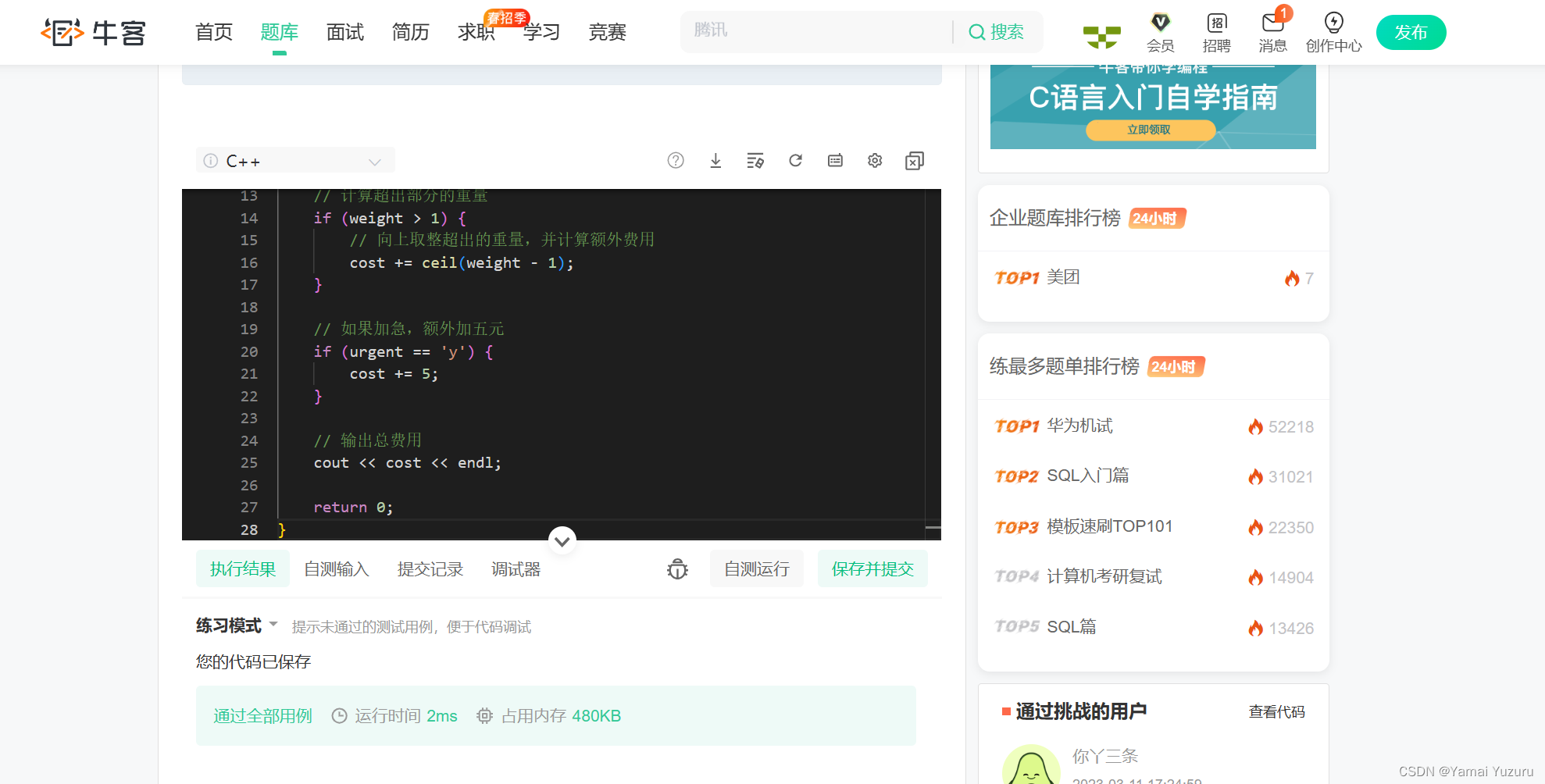
代码
import java.io.*;
class Main{
static int N = 100010;
static int n,k;
static int[] h = new int[N];
static int[] w = new int[N];
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] s = in.readLine().split(" ");
n = Integer.parseInt(s[0]);
k = Integer.parseInt(s[1]);
int max = 0; // 应该取max,而不是min,有些巧克力小但是可以不用
for(int i=0;i<n;i++){
s = in.readLine().split(" ");
h[i] = Integer.parseInt(s[0]);
w[i] = Integer.parseInt(s[1]);
max = Math.max(max,h[i]);
max = Math.max(max,w[i]);
}
int l = 1,r = max; // 取0是因为r=max可能为1,进不去while.好像也可以,输入保证了每个都可以分得1*1
while(l<r){
int mid = l+r+1>>1;
if(check(mid)) l = mid;
else r = mid-1;
}
System.out.println(r);
}
public static boolean check(int u){ // 判断如果要分成u*u可不可以
int count = 0;
for(int i=0;i<n;i++){ // 计算所有能分成u*u的巧克力快数
count += (w[i]/u)*(h[i]/u);
}
if(count<k) return false; // 不够分
else return true;
}
}