#论文题目：【序列推荐】SR-GNN: Session-based Recommendation with Graph Neural Networks（SR-GNN:基于会话的图神经网络推荐）
#论文地址：https://arxiv.org/abs/1811.00855
#论文源码开源地址： https://github.com/CRIPAC-DIG/SR-GNN
#论文所属会议：AAAI 2019
#论文所属单位：中科院

1.导读

SR-GNN是中科院提出的一种基于会话序列建模的推荐系统，这里所谓的会话是指用户的交互过（每个会话表示一次用户行为和对应的服务，所以每个用户记录都会构建成一张图），这里说的会话序列应该是专门表示一个用户过往一段时间的交互序列。 基于会话的推荐是现在比较常用的一种推荐方式，比较常用的会话推荐包括 循环神经网络、马尔科夫链。但是这些常用的会话推荐方式有以下的两个缺点

• 当一个会话中用户的行为数量十分有限时【就是比较少时】，这种方法较难捕获用户的行为表示。比如使用RNN神经网络进行会话方式的推荐建模时，如果前面时序的动作项较少，会导致最后一个输出产生推荐项时，推荐的结果并不会怎么准确。
• 根据以往的工作发现，物品之前的转移模式在会话推荐中是十分重要的特征，但RNN和马尔科夫过程只对相邻的两个物品的单项转移向量进行 建模，而忽略了会话中其他的物品。【意思是RNN那种方式缺乏整体大局观，只构建了单项的转移向量，对信息的表达能力不够强】

首先在解读论文的时候，需要明白序列召回的输入和输出是什么，一般来说序列召回输入的是用户的行为序列(用户交互过的item id的列表),需要预测的是用户下一个时刻可能点击的top-k个item。那在实际操作的过程中，我们通常把用户的行为序列抽取成一个用户的表征向量，然后和Item的向量通过一些ANN的方法来进行快速的检索，从而筛选出和用户表征向量最相似的top-k个Item。我们下面介绍的SR-GNN就是完成了上述的两个流程

1.1 模型结构

这里我们可以看到，我们对输入的用户的行为序列提取出用户的向量表征进行了如下的处理：

• 1.将用户的行为序列构造成 Session Graph
• 2.我们通过GNN来对所得的 Session Graph进行特征提取，得到每一个Item的向量表征
• 3.在经过GNN提取Session Graph之后，我们需要对所有的Item的向量表征进行融合，以此得到User的向量表征
  在得到了用户的向量表征之后，我们就可以按照序列召回的思路来进行模型训练/模型验证了，下面我们来探讨这三个点如何展开

1.2 构建Session Graph

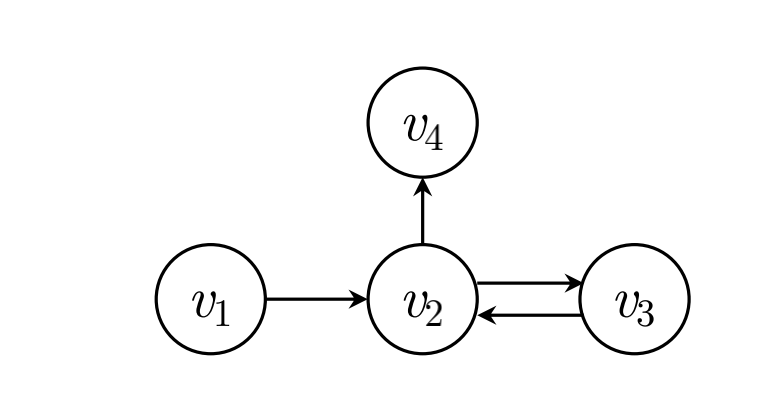
这里首先需要根据用户的行为序列来进行构图，这里是针对每一条用户的行为序列都需要构建一张图，构图的方法也非常简单，我们这里将其视作是有向图，如果$v_2$和$v_1$在用户的行为序列里面是相邻的，并且$v_2$在$v_1$之后，则我们连出一条从$v_2$到$v_1$的边，按照这个规则我们可以构建出一张图。(下面是论文中给的样例图)

这里为什么将每个用户的行为都包装成一个图，是因为如果将所有用户对商品的交互关系都放在一张图中，会导致对用户独特兴趣捕捉上的混乱，所以需要单独构建，而且这样构建的优势是后续训练时候，每一行样本都可以构建成一张图，还是比较方便的。

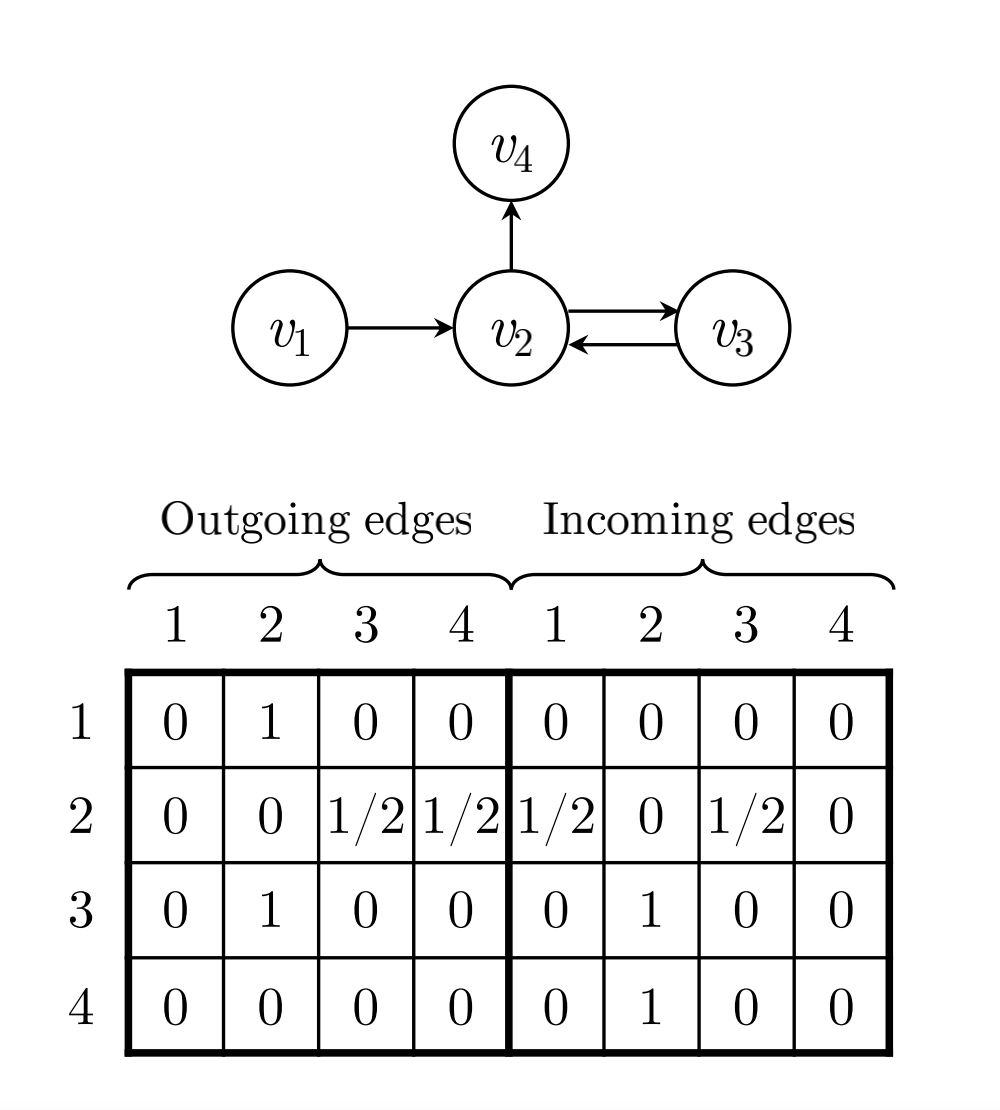
在完成构图之后，我们需要使用变量来存储这张图，这里用$A_s$来表示构图的结果，这个矩阵是一个$(d,2d)$的矩阵 ，其分为一个$(d,d)$的Outing矩阵和一个$(d,d)$的Incoming矩阵对于Outing矩阵，直接去数节点向外伸出去的边的条数，如果节点向外伸出的节点数大于1，则进行归一化操作(例如节点$v_2$向外伸出了两个节点$v_3,v_4$，则节点$v_2$到节点$v_3,v_4$的值都为0.5)。Incoming矩阵同理

1.3 通过GNN学习Item的向量表征

这一部分我们主要关注如何从图中学习到Item的向量表征,这里设$v_i^t$表示在第t次GNN迭代后的item i的向量表征，$A_{s,i}\in R^{1\times 2n}$表示$A_s$矩阵中的第$i$行，即代表着第$i$个item的相关邻居信息。则我们这里通过公式(1)来对其邻居信息进行聚合，这里主要通过矩阵$A_{s,i}$和用户的序列$[v_1^{t-1},...,v_n^{t-1}{]}^T\in R^{n\times d}$的乘法进行聚合的，不过要注意这里的公式写的不太严谨，实际情况下两个$R^{1\times 2n}和R^{n\times d}$的矩阵是无法直接做乘法的，在代码实现中，是将矩阵A分为in和out两个矩阵分别和用户的行为序列进行乘积的

$$a_{s,i}^t=A_{s,i}[v_1^{t-1},...,v_n^{t-1}{]}^T\text{H}+b\text{\hspace{1em}(1)}$$

'''
A : [batch,n,2n] 图的矩阵
hidden : [batch,n,d] 用户序列的emb
in矩阵：A[:, :, :A.size(1)]
out矩阵：A[:, :, A.size(1):2 * A.size(1)]
inputs : 就是公式1中的 a 
'''
input_in = paddle.matmul(A[:, :, :A.shape[1]], self.linear_edge_in(hidden)) + self.b_iah
input_out = paddle.matmul(A[:, :, A.shape[1]:], self.linear_edge_out(hidden)) + self.b_ioh
# [batch_size, max_session_len, embedding_size * 2]
inputs = paddle.concat([input_in, input_out], 2)

在得到公式(1)中的$a_{s,i}^t$之后，根据公式(2)(3)计算出两个中间变量$z_{s,i}^t,r_{s,i}^t$可以简单的类比LSTM，认为$z_{s,i}^t,r_{s,i}^t$分别是遗忘门和更新门

$$z_{s,i}^t=\sigma (W_z{a}_{s,i}^t+U_z{v}_i^{t-1})\in R^d\text{\hspace{1em}(2)}$$

$$r_{s,i}^t=\sigma (W_r{a}_{s,i}^t+U_r{v}_i^{t-1})\in R^d\text{\hspace{1em}(3)}$$

这里需要注意，我们在计算$z_{s,i}^t,r_{s,i}^t$的逻辑是完全一样的，唯一的区别就是用了不同的参数权重而已.
在得到公式(2)(3)的中间变量之后,我们通过公式(4)计算出更新门下一步更新的特征，以及根据公式(5)来得出最终结果

$${v_i^t}^{\sim }=tanh(W_o{a}_{s,i}^t+U_o(r_{s,i}^t\odot v_i^{t-1}))\in R^d\text{\hspace{1em}(4)}$$

$$v_i^t=(1-z_{s,i}^t)\odot v_i^{t-1}+z_{s,i}^t\odot {v_i^t}^{\sim }\in R^d\text{\hspace{1em}(5)}$$

这里我们可以看出，公式(4)实际上是计算了在第t次GNN层的时候的Update部分，也就是${v_i^t}^{\sim }$,而在公式(5)中通过遗忘门$z_{s,i}^t$来控制第t次GNN更新时，$v_i^{t-1}$和${v_{i}^{t}}{\sim} $所占的比例。这样就完成了GNN部分的item的表征学习

这里在写代码的时候要注意，对于公式(3)(4)(5)，我们仔细观察，对于$a_{s,i}^t,v_i^{t-1}$这两个变量而言，每个变量都和三个矩阵进行了相乘，这里的计算逻辑相同，所以将$Wa,Uv$当作一次计算单元，在公式(3)(4)(5)中，均涉及了一次这样的操作，所以我们可以将这三次操作放在一起做，然后在讲结果切分为3份，还原三个公式，相关代码如下

'''
inputs : 公式(1)中的a
hidden : 用户序列，也就是v^{t-1}
这里的gi就是Wa，gh就是Uv，但是要注意这里不该是gi还是gh都包含了公式3~5的三个部分
'''

# gi.size equals to gh.size, shape of [batch_size, max_session_len, embedding_size * 3]

gi = paddle.matmul(inputs, self.w_ih) + self.b_ih
gh = paddle.matmul(hidden, self.w_hh) + self.b_hh
# (batch_size, max_session_len, embedding_size)
i_r, i_i, i_n = gi.chunk(3, 2)   # 三个W*a
h_r, h_i, h_n = gh.chunk(3, 2)   # 三个U*v
reset_gate = F.sigmoid(i_r + h_r)  #公式(2)
input_gate = F.sigmoid(i_i + h_i)  #公式(3)
new_gate = paddle.tanh(i_n + reset_gate * h_n)  #公式(4)
hy = (1 - input_gate) * hidden + input_gate * new_gate  # 公式(5)

1.4 生成User 向量表征(Generating Session Embedding)

在通过GNN获取了Item的嵌入表征之后，我们的工作就完成一大半了，剩下的就是讲用户序列的多个Item的嵌入表征融合成一个整体的序列的嵌入表征

这里SR-GNN首先利用了Attention机制来获取序列中每一个Item对于序列中最后一个Item $v_n(s_1)$的attention score，然后将其加权求和，其具体的计算过程如下

$$\begin{gathered} a_i={\text{q}}^T\sigma (W_1{v}_n+W_2{v}_i+c)\in R^1 \\ {s}_g=\sum _{i=1}^n{a}_i{v}_I\in R^d\text{\hspace{1em}(6)} \end{gathered}$$

在得到$s_g$之后，我们将$s_g$与序列中的最后一个Item信息相结合，得到最终的序列的嵌入表征

$$s_h=W_3[s_1;s_g]\in R^d\text{\hspace{1em}(7)}$$

'''
seq_hidden : 序列中每一个item的emb
ht ： 序列中最后一个item的emb，就是公式6~7中的v_n(s_1)
q1 : 公式(6)中的 W_1 v_n
q2 : 公式(6)中的 W_2 v_i 
alpha : 公式(6)中的alpha
a : 公式(6)中的s_g
'''
seq_hidden = paddle.take_along_axis(hidden,alias_inputs,1)
# fetch the last hidden state of last timestamp
item_seq_len = paddle.sum(mask,axis=1)
ht = self.gather_indexes(seq_hidden, item_seq_len - 1)
q1 = self.linear_one(ht).reshape([ht.shape[0], 1, ht.shape[1]])
q2 = self.linear_two(seq_hidden)

alpha = self.linear_three(F.sigmoid(q1 + q2))
a = paddle.sum(alpha * seq_hidden * mask.reshape([mask.shape[0], -1, 1]), 1)
user_emb = self.linear_transform(paddle.concat([a, ht], axis=1))

至此我们就完成了SR-GNN的用户向量生产了，剩下的部分就可以按照传统的序列召回的方法来进行了

参考：https://aistudio.baidu.com/aistudio/projectdetail/5313491