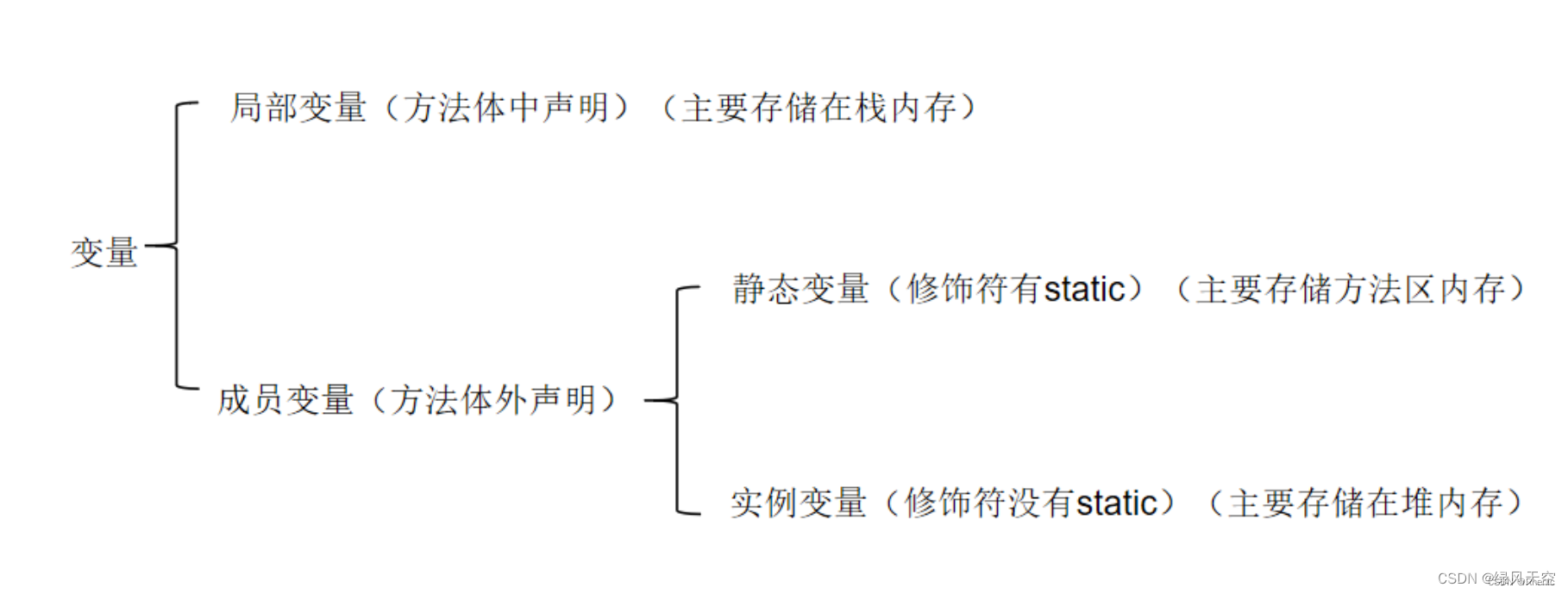
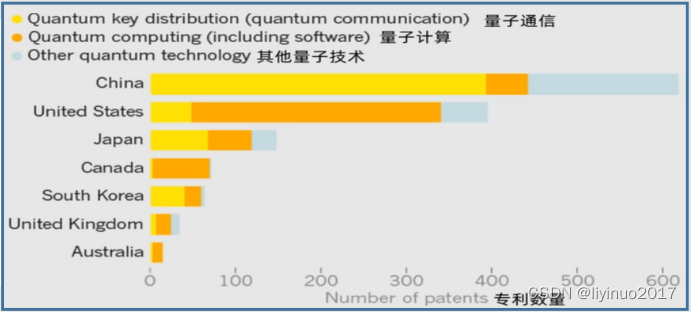
DWR用到复杂数据集中。

看了一半发现一个博客将的也不错放在这里Deep Stable Learning for Out-Of-Distribution Generalization_六点先生的博客-CSDN博客_随机傅里叶特征

目标任务：

一般假设（训练数据的已知异质性（如领域标签）或不同领域的能力大致相等）都不成立的条件下，找特征和标签的真实联系。

现有方法：DWR（[29][51]）

优化扩展：

现有DWR使用在线性模型，扩展到深度模型中以处理更复杂的数据类型如图像时

面临主要挑战【StableNet解决方法】：

1）特征之间复杂的非线性依赖关系比线性依赖关系更难被测量和消除

--提出了一种基于随机傅里叶特征[45]的具有线性计算复杂性的新型非线性特征去关联方法

2）方法中的全局样本加权策略在深度模型中需要过多的存储和计算成本，这在实践中是不可行的。

--提出了一个高效的优化机制，通过迭代保存和重新加载模型的特征和权重，在全局范围内感知和消除相关性。

理论分析：

1.基于cross-covariance operator和随机傅里叶特征（RFF）的独立性条件()

1.交叉协方差算子

考虑在随机变量A的域上有一个可测的、正定的内核kA，相应的RKHS用HA来表示。如果kB和HB的定义相似，那么从HB到HA的交叉协方差算子ΣAB[13]如下。

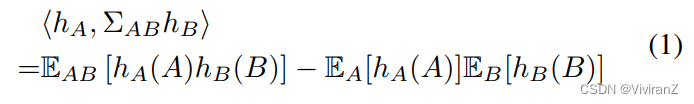
交叉协方差算子计算的准则HSIC过于复杂于是简化版：

后面直接看的前引的博客了

后面补一下附录、RFF等内容再回来吧

全文翻译

【摘要】

当测试数据和训练数据具有相似的分布时，基于深度神经网络的方法取得了惊人的性能，但在其他情况下会明显失败。因此，消除训练和测试数据之间的分布变化的影响，对于建立有性能前景的深度模型至关重要。通常的方法是假定训练数据的已知异质性（如领域标签）或不同领域的能力大致相等。在本文中，我们考虑了一种更具挑战性的情况，即上述两种假设都不成立。我们建议通过学习训练样本的权重来消除特征之间的依赖关系，这有助于深度模型摆脱虚假的相关性，反过来，更专注于鉴别性特征和标签之间的真正联系，来解决这个问题。广泛的实验清楚地证明了我们的方法在多个分布泛化基准上与最先进的对应部分相比的有效性。通过对包括PACS、VLCS、MNIST-M和NICO在内的分布泛化基准的广泛实验，我们展示了我们的方法与最先进的同行相比的有效性。

【Introduction】

许多机器学习方法倾向于利用训练分布中存在的微妙的统计相关性进行预测，这在I.I.D.假设下被证明是有效的，即测试和训练数据是从相同的分布中独立采样的。然而，在实际情况下，由于真实数据的复杂生成机制，如数据选择偏差、混杂因素或其他特殊性，这种假设很难得到满足[5, 54, 12, 47, 21]。测试分布可能会发生与训练分布不受控制的未知偏移，这使得大多数机器学习模型无法做出值得信赖的预测[2, 51]。为了解决这个问题，提出了分布外泛化（OOD），以提高模型在分布偏移下的泛化能力[55, 27]。

从本质上讲，当发生分布转移时，当前模型的准确率下降主要是由不相关特征（即与特定类别无关的特征，如上下文特征、人物风格等）和类别标签之间的虚假关联造成的，而这种虚假关联是由不相关特征和相关特征（即与特定类别相关的特征）之间的微妙关联内在地造成的[30, 38, 35, 2]。以 "狗 "类别的识别任务为例，如图1所示，如果狗在大多数训练图像中都在水中，那么狗和水的视觉特征会有很强的相关性，从而导致水的视觉特征与 "狗 "标签之间的虚假相关性。因此，当遇到没有水的狗或有水的其他物体（如猫）的图像时，该模型很容易产生错误的预测。

最近，这种分布（域）转移问题在域泛化（DG）文献中得到了深入研究[41, 17, 25, 62, 31, 33]。DG的基本思想是将一个类别划分为多个领域，使不相关的特征在不同的领域中变化，而相关的特征保持不变[25, 34, 40]。这样的训练数据使得一个精心设计的模型有可能学习跨领域的不变表征，并抑制来自不相关特征的负面影响，从而在分布转变的情况下获得更好的泛化能力。一些开创性的方法需要明确和显著的异质性，即领域是手工划分和标记的[61, 16, 46, 9, 42]，这在实际应用中不能总是得到满足。最近，一些方法被提出来从数据中隐含地学习潜域[44, 39, 60]，但它们隐含地假设潜域是平衡的，也就是说，训练数据是由潜域的平衡抽样形成。然而，在实际案例中，域平衡的假设很容易被违反，导致这些方法的退化。这在我们的实验中也得到了经验上的验证，如第4节所示。

在这里，我们考虑了一个更加现实和具有挑战性的环境，即训练数据的领域是未知的，我们不隐含地假设潜在领域是平衡的。为了这个目标，我们提出了一个关于稳定学习的研究方向[50, 28]。鉴于相关特征和不相关特征之间的统计依赖性是分布变化下模型崩溃的主要原因，他们提出通过去相关相关和不相关特征来实现分布外泛化。由于没有额外的监督来分离相关特征和不相关特征，一个保守的解决方案是对所有特征进行装饰。最近，这一概念已经被证明可以有效地提高线性模型的泛化能力。[29]提出了一种以装饰输入变量为目标的样本加权方法，[51]从理论上证明了为什么这种样本加权可以使线性模型在分布变化下产生稳定的预测。但它们都是在线性框架的约束下开发的。当把这些想法扩展到深度模型中以处理更复杂的数据类型如图像时，我们面临着两个主要的挑战。首先，特征之间复杂的非线性依赖关系比线性依赖关系更难被测量和消除。其次，这些方法中的全局样本加权策略在深度模型中需要过多的存储和计算成本，这在实践中是不可行的。

为了解决这两个挑战，我们提出了一个名为StableNet的方法。就第一个挑战而言，我们提出了一种基于随机傅里叶特征[45]的具有线性计算复杂性的新型非线性特征去关联方法。至于第二个挑战，我们提出了一个高效的优化机制，通过迭代保存和重新加载模型的特征和权重，在全局范围内感知和消除相关性。这两个模块在我们的方法中被联合优化。此外，如图1所示，StableNet可以有效地将不相关的特征（如水）部分剔除，并利用真正相关的特征进行预测，从而在野外非平稳环境中获得更稳定的表现。

【相关工作】

领域泛化。领域泛化（DG）考虑了用多个源域训练的深度模型对未见过的领域的泛化能力。一个常见的方法是在多个源域中提取领域变量特征[17, 25, 32, 34, 40, 10, 22, 43, 48, 40]，或者聚合特定领域的模块[36, 37]。有几项工作提出通过增加源域来扩大可用数据空间[6, 49, 59, 44, 64, 63]。有几种方法利用元学习的正则化[33, 10]和不变风险最小化（IRM）框架[2]进行危险分析。尽管DG方法在精心设计的实验环境中取得了可喜的成果，但一些强有力的假设，如人工划分和标记的领域以及每个领域的平衡采样过程，实际上阻碍了DG方法的实际应用。

特征相关性。由于特征之间的相关性会影响甚至损害模型的预测效果，一些工作集中在训练过程中消除这种相关性。一些基于Lasso框架的开创性工作[56,7]提出通过添加一个正则器，使高度相关的特征不被同时选择，来实现特征的去重。最近，有几项工作从理论上弥补了相关性和错误指定下的模型稳定性之间的联系[51, 29]，并建议通过样本重配方案来解决这样的问题。然而，上述方法都是在线性框架下开发的，无法处理计算机视觉应用中的图像和视频等复杂数据类型。更多相关工作和讨论见附录A

【3. Sample Weighting for Distribution Generalization】

我们通过对样本进行全局加权来解决分布偏移的问题，直接对每个输入样本的所有特征进行去重，从而消除了相关和不相关特征之间的统计关联性。具体来说，StableNet通过利用随机傅里叶特征（RFF）和样本加权的特点，摆脱了特征之间的线性和非线性依赖。为了使全局相关性方法适用于现代深度模型，我们进一步提出了全局相关性的保存和重载机制，以减少训练数据规模较大时的存储和计算成本的使用。在第3.1节中，我们展示了这些公式和理论解释。在第3.2节中，我们介绍了保存和重载全局相关的方法，它使深度模型的全局相关计算成为可能。符号 X⊂R mX表示原始像素空间，Y⊂R mY表示结果空间，Z⊂R mZ表示表示空间。mX，mY，mZ分别是空间X，Y，Z的维度。我们有n个样本X⊂R n×mX，标签Y⊂R n×mY，我们用Xi和yi来表示第i个样本。由神经网络学习的表征被捐赠为Z ⊂R n×mZ，表征空间中的第i个变量被记为Z:,i。

3.1. Sample weighting with RFF

独立性检验统计

为了消除表示空间中任何一对特征Z:,i和Z:,j之间的依赖性，我们引入了衡量随机变量之间独立性的假设检验统计。假设有两个一维随机变量A、B(这里为了简化符号，我们用A和B来表示随机变量，而不是Z:,i和Z:,j。)，我们分别从A和B的分布中抽取(A1, A2, ... An)和(B1, B2, ... Bn) 。主要问题是这两个变量基于样本的相关性如何。

考虑在随机变量A的域上有一个可测的、正定的内核kA，相应的RKHS用HA来表示。如果kB和HB的定义相似，那么从HB到HA的交叉协方差算子ΣAB[13]如下。

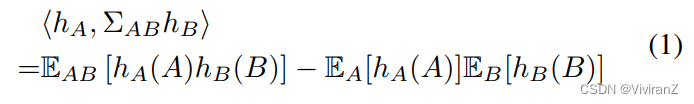
对于所有hA∈HA和hB∈HB。那么，可以通过以下命题来确定独立性[14]

希尔伯特-施密特独立准则（HSIC）[18]，要求ΣAB的平方希尔伯特-施密特准则应该为零，可以作为一个标准来确保特征去重[3]。然而，HSIC的计算需要明显的计算成本，并且随着训练数据批处理量的增加而增加，所以它无法在大数据集上训练深度模型。附录B.2中讨论了更多的独立性测试方法。实际上，Frobenius规范对应于欧几里得空间中的Hilbert[1]Schmidt规范[53]，因此，独立测试统计量可以基于Frobenius规范。

这里我们分别从HRFF中抽取nA和nB函数，HRFF表示随机傅里叶特征的函数空间，其形式如下

即ω是从标准正态分布中取样的，φ是从均匀分布中取样的。然后，独立性检验统计量IAB被定义为部分交叉协方差矩阵的Frobenius规范，即I

注意，IAB总是非负的。当IAB减小到零时，两个变量A和B趋于独立。因此，IAB可以有效地衡量随机变量之间的独立性。独立性测试的准确性随着nA和nB的增加而增长。根据经验，将nA和nB都设为5，就足以判断随机变量的独立性[53]。

学习用于去相关的样本权重

受[29]的启发，我们建议通过样本加权来消除表征空间中特征之间的依赖性，并通过RFF衡量一般的独立性。

我们用w∈R^n_+来表示样本权重，\Sigma^n_{i=1} w_i = n。加权后，方程3中随机变量A和B的部分交叉协方差矩阵可以计算如下。

这里u和v是方程4中解释的RFF映射函数。StableNet的目标是任何一对特征之间的独立性。具体来说，对于特征Z:,i和Z:,j，相应的部分交叉协方差矩阵应该是Σˆ Z:,iZ:,j ;w 2 F，如公式6所示。我们建议通过以下方式来优化w

其中 ∆n = w∈R n + | Pn i=1 wi = n 。因此，用最优的w∗对训练样本进行加权，可以最大程度地缓解特征之间的依赖性。

一般来说，我们的算法会反复优化样本权重w、表示函数f和预测函数g，具体如下。

其中Z（t+1）=f（t+1）（X），L（-，-）代表交叉熵损失函数，t代表时间戳。最初，w（0）=（1，1，...，1）T。

3.2. 全局学习样本权重

方程8要求为每个样本学习一个特定的权重。然而，在实践中，特别是对于深度学习任务，需要巨大的存储和计算成本来全局学习样本权重。此外，使用SGD进行优化，每批中只有部分样本被观察到，因此无法学习所有样本的全局权重。在这一部分，我们提出了一种保存和重载的方法，它合并和保存训练阶段遇到的特征和样本权重，并将它们作为所有训练数据的全局知识重新加载，以优化样本权重。

对于每个批次，用于优化样本权重的特征产生如下。ZO = Concat(ZG1, ZG2, - -, ZGk, ZL), wO = Concat(wG1, wG2, - -, wGk, wL) 。(9) 这里我们略微滥用了符号ZO和wO，分别指用于优化新样本权重的特征和权重，ZG1, - -, ZGk, wG1, - -, wGk是全局特征和权重，在每批结束时更新，代表整个训练数据集的全球信息。ZL和wL是当前批次的特征和权重，代表本地信息。方程9中合并所有特征的操作是沿着样本的串联操作，即如果批次大小为B，则ZO是一个大小为（（k+1）B）×mZ的矩阵，wO是一个（（k+1）B）维的矢量。通过这种方式，我们将存储和计算成本从O(N)减少到O(kB)。在每个批次的训练中，我们保持wGi固定不变，只有wL在方程8下是可学习的。在每个迭代训练结束时，我们将全局信息（ZGi，wGi）和局部信息（ZL，wL）融合如下。Z′ Gi = αiZGi + (1 - αi)ZL, w′ Gi = αiwGi + (1 - αi)wL. (10) 这里对于每组全局信息（ZGi, wGi），我们使用k个不同的平滑参数αi来考虑全局信息中的长期记忆（αi大）和短期记忆（αi小），k表示预存特征是原始特征的k倍。最后，我们用(Z′Gi, w′Gi)代替所有的(ZGi, wGi)，进行下一批的训练。

在训练阶段，我们用公式8迭代优化样本权重和模型参数。在推理阶段，预测模型直接进行预测，无需计算样本权重。我们方法的详细过程见附录B.1。

4. Experiments

4.1. Experimental settings and datasets

我们在各种环境中验证了StableNet。为了涵盖更普遍和具有挑战性的分布转移情况，我们采用了以下四种实验设置。

不平衡。在常见的DG设置中，源域的能力被假定为是可比较的。然而，考虑到大多数数据集是潜在未知域的混合物，我们很难假设这些域的样本量是一致的，因为这些数据集不是由潜在域的平均采样产生的。我们用这种设置来模拟这种情况。领域被分成了源领域和目标领域。各个域的能力可以有很大的不同。请注意，这种设置，即可用领域的能力是不平衡的，而每个类别的比例在各领域中保持一致，与类不平衡问题的设置完全不同。这种设置是为了评估异质性不明确且不明显时模型的泛化能力。

灵活。我们考虑一个更具挑战性但在现实世界中很常见的设置，不同类别的领域可以是多种多样的。例如，鸟类可以在树上，但几乎不在水中，而鱼类则相反。如果我们把图像中的背景作为领域划分的指标，"鸟 "类的图像可以划分为 "树上 "的领域，但不能划分为 "水中 "的领域，而 "鱼 "类的图像则不然，从而导致不同类别中领域的多样性。因此，这种设置模拟了现实世界中广泛存在的场景。在这种情况下，不同类别的分布转移水平不同，鉴于相关特征和类别相关特征之间的统计关联性不同，需要很强的概括能力。

对抗性。我们考虑最具挑战性的情景，即模型受到对抗性攻击，域和标签之间的虚假关联性很强且具有误导性。例如，我们假设在训练数据中，类别 "狗 "通常与领域 "草 "相关，类别 "猫 "与领域 "沙发 "相关，而在测试数据中，类别 "狗 "通常与领域 "沙发 "相关，类别 "猫 "与领域 "草 "相关。如果 "狗 "类图像中域 "草 "的比例明显高于其他图像，预测模型可能倾向于将草识别为狗。

经典。这个设置与DG中的普通设置相同。各个领域的能力是相当的。因此，当训练数据的异质性很明显时，这种设置是用来评估模型的泛化能力的，与前三种设置相比，这种设置的挑战性较小。

数据集。我们考虑用四个数据集来贯穿这四个设置，即PACS[31]、VLCS[58]、MNIST-M[15]和NICO[20]。这些数据集的介绍和实施细节见附录C.1。

4.2. 不平衡的设置

鉴于这种设置要求数据集中的所有类别共享相同的候选域集，这与NICO不相容，我们在这种设置中采用PACS和VLCS。三个域被视为源域，另一个域被视为目标域。为了使来自异质来源的数据量得到明确区分，我们将一个域设定为主导域。对于每个目标域，我们从源域中随机选择一个域作为主导的源域，并调整主导域和其他两个域的数据比例。比率和分区的细节见附录C.2。

这里我们在表1中展示了当三个源域的容量比为5:1:1时的结果，我们的方法在PACS和VLCS的所有目标域都优于其他方法。此外，如附录C.2所示，StableNet在所有其他比例下都能持续取得最佳性能。这些结果表明，相关特征和不相关特征之间微妙的统计相关性足以严重损害跨领域的概括性。当相关关系被消除后，模型能够学习到相关特征和标签之间的真正联系，并只根据它们进行推理，因此泛化效果更好。对于像DGMMLD[39]这样的对抗性训练方法，来自次要领域的监督是不充分的，模型区分不相关特征的能力受到影响。对于基于源域的增强方法，如M-ADA[44]，主导域的影响并没有减少，而次要域在增强后仍然不重要。像RSC[23]这样的方法采用正则化来防止模型在源域上过度拟合，来自次要域的样本可以被认为是离群值而被忽略。因此，相关特征和不相关特征之间的微妙关联，特别是在次要领域，并没有被消除。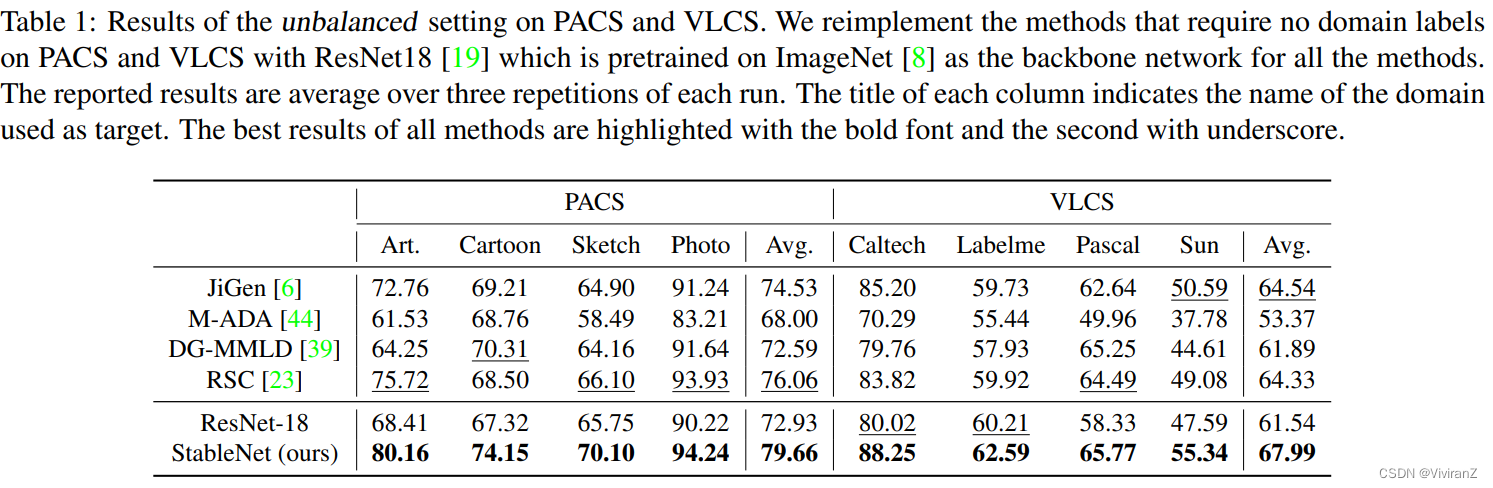

4.3. 非平衡+灵活设置

我们采用PACS、VLCS和NICO来评估非平衡+灵活设置。对于PACS和VLCS，我们随机选择一个域作为每个类的主导域，另一个域作为目标。对于NICO，每个类有10个域，其中8个被选为源，2个被选为目标。我们调整主导域与次要域的比例，以调整分布偏移的程度。这里我们报告的是主导比例为5：1：1时的结果。其他划分的细节和更多结果见附录C.3。

结果显示在表2中。在这种设置下，M-ADA和DGMMLD在NICO上的表现未能优于ResNet-18。M-ADA是用自动编码器生成图像进行训练的，当训练数据是大尺度的真实世界的图像，并且分布偏移不是由随机干扰引起时，它可能会失败。DG-MLD通过聚类生成域标签，当数据缺乏明确的异质性或者潜伏域的数量对于聚类来说太大，可能会失败。相比之下，当输入数据具有复杂的结构，特别是来自无限资源的真实世界的图像时，StableNet显示出强大的泛化能力。StableNet可以捕捉各种形式的依赖关系，并平衡输入数据的分布。在PACS和VLCS上，StableNet的表现也超过了最先进的方法，显示了去除特征之间的统计依赖性的有效性，特别是当不同类别的源域不一致时。更多的实验结果请见附录C.3。

4.4. 不平衡+灵活+对抗性设置

为了利用各种水平的对抗性攻击的效果，我们采用MNIST-M来评估我们的方法，因为MNIST-M中有许多（200个）可选域。PACS和VLCS中的域不足以产生多个对抗水平。因此，我们用三条规则生成了一个新的MNIST-M数据集。1）对于一个给定的类别，训练和测试中的域之间没有重叠；2）为训练集中的每个类别随机选择一个背景图像，在同一图像中裁剪的上下文被分配为测试数据中另一个类别的主导上下文（域），这样标签和域之间就有了强烈的虚假关联；3）主导上下文和其他上下文的比例从9.5：1到1：1不等，以产生具有不同水平分布偏移的设置。详细的数据生成方法、采用的骨干网络和样本图像见附录C.4。

结果显示在表3中。随着主导比率的增加，领域和类别之间的虚假关联性变得更强，因此预测模型的性能下降了。当视觉特征的不平衡很严重时，我们的方法与基线方法相比取得了明显的改善。对于基于正则化的方法，如RSC，它们倾向于削弱来自次要领域的监督，这些领域可能被认为是离群的，因此在对抗性攻击下，不相关的特征和标签之间的虚假关联会加强，导致与vanilla ResNet模型相比结果更差。如表3所示，RSC未能超越vanilla CNN的表现。

4.5. 经典设置

经典设置与DG中的普通设置相同。网域被分成源网域和目标网域。各个域的能力是可以比较的。鉴于这种设置要求数据集中的所有类都共享相同的候选域集，这与NICO不兼容，我们在这种设置中采用PACS和VLCS。我们对两个数据集都采用了[6, 39]的实验方案，利用三个域作为源域，其余一个域作为目标域。

实验结果如表4所示。在VLCS上，StableNet在四个目标案例中的两个案例中超过了其他最先进的方法，并获得了最高的平均准确率。在PACS上，StableNet在目标域 "照片 "上取得了最高的准确率，与最先进的方法RSC相比，平均准确率相当（低0.46%）。StableNet和基线之间的准确率差距表明，即使来自不同源域的样本数量大致相同，相关特征和不相关特征之间微妙的统计相关性仍然很强，当消除了这些相关性后，模型在不同领域的概括性更好。

4.6. 消融研究

StableNet依靠从高斯采样的随机傅里叶特征来平衡训练数据。取样的特征越多，最终的表征就越独立。然而，在实践中，生成更多的特征需要更多的计算成本。在这项消融研究中，我们利用了随机傅里叶特征的采样大小的影响。此外，受[57]的启发，我们可以通过随机选择用于计算不同比率的依赖性的特征来进一步降低特征维度。图3显示了不同维度的随机傅里叶特征的StableNet的结果。如果我们去掉所有的随机傅立叶特征，我们方程7中的正则器就会退化，只能对特征间的线性相关进行建模。图2(a)展示了消除表征间非线性依赖的有效性。从图2(b)来看，非线性依赖在视觉特征中很常见，使深度模型无法学习输入图像和类别标签之间的真实依赖。

我们进一步利用方程9中预存特征的大小和权重的影响，结果如图2（c）所示。当预存特征的大小减少到0时，在每个批次中学习样本权重，产生明显的差异。一般来说，随着预存大小的增加，准确率略有提高，方差明显下降，说明预存特征有助于全局学习样本权重，因此模型的泛化能力更加稳定。

4.7. 显著性地图

对图像分类模型的一个直观的解释类型是识别对最终决定有很大影响的像素[52]。为了证明模型在进行预测时是关注对象还是关注背景（领域），我们将类分函数相对于输入像素的梯度可视化。在稳定学习的情况下，我们对所有的方法采用相同的骨干结构，这样我们就采用了[1]所建议的平滑梯度，它生成的显著性地图取决于模型的学习参数而不是结构。图4显示了可视化的结果。基线模型的显著性地图显示，各种背景吸引了分类器的明显关注，而对我们的模型却没有做出决定性的贡献。更多的可视化结果见附录C.6，它进一步证明了StableNet更关注于视觉部分，当物体的姿势或位置发生变化时，这些视觉部分是有区别的，并且是不变的。