文章目录
- 1.计算图
- 2.反向传播
- 2.1 链式求导法则
- 2.2 反向传播过程
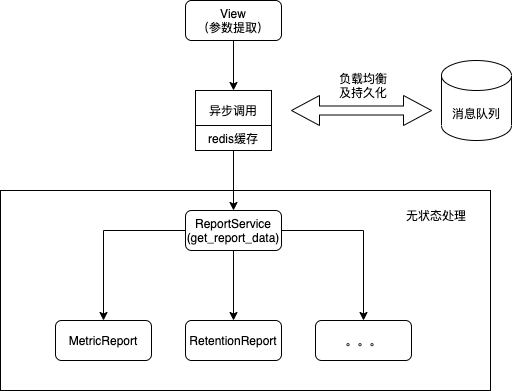
- 3.Pytorch中前馈和反馈的计算
- 3.1 Tensor
- 3.2 代码演示
对于简单的模型,梯度变换可以用解析式表达进行手算,但是复杂模型(很多w,b)的损失函数需要挨个写解析式,非常不好计算(主要是求导)。因此,可以考虑使用某种算法,把整个网络看做一个计算图,在图上传播整个梯度。这种算法,就称为反向传播算法。
转载:梯度下降法是通用的优化算法,反向传播法是梯度下降法在深度神经网络上的具体实现方式。
1.计算图
单层
需要注意的是,神经网络的训练本质,就是对每层的w和b进行训练。
 每一层的结束都需要引入非线性的激活函数。
每一层的结束都需要引入非线性的激活函数。
如果不加入激活函数,那么无论多少层,得到的结果都是线性的。

2.反向传播
2.1 链式求导法则
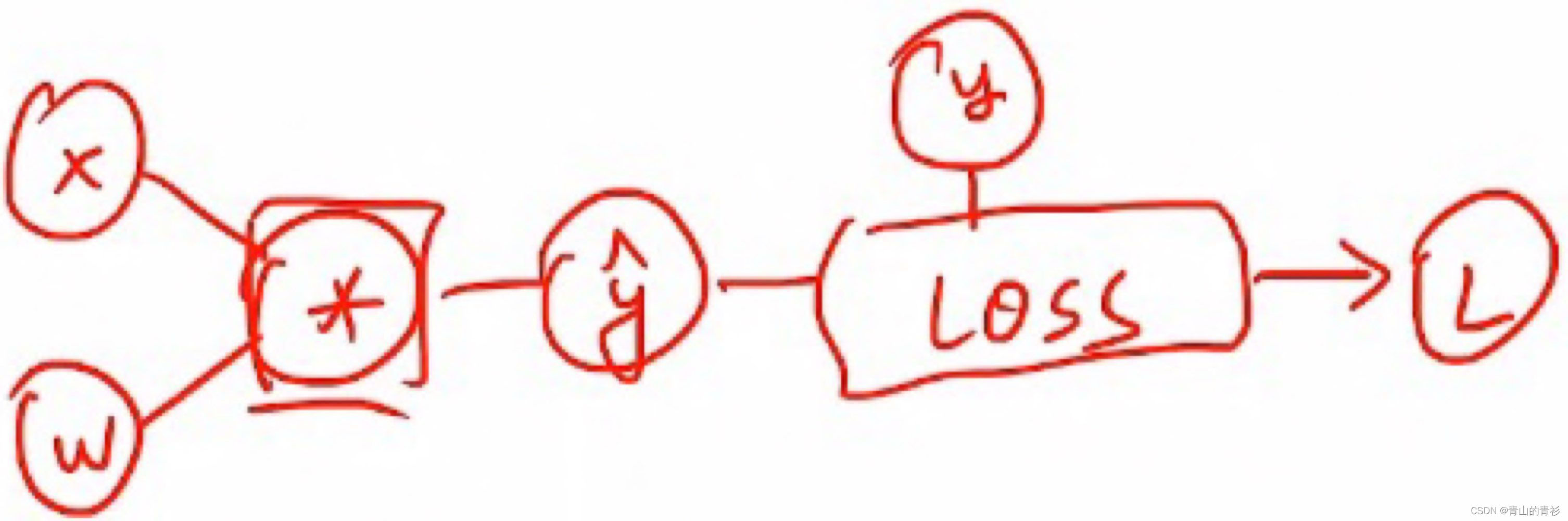
进行反向传播的关键就是链式求导。反向传播其实就是计算图中的梯度求解,通过链式求导得到L对x和w的导数(梯度),再根据更新规则进行更新。
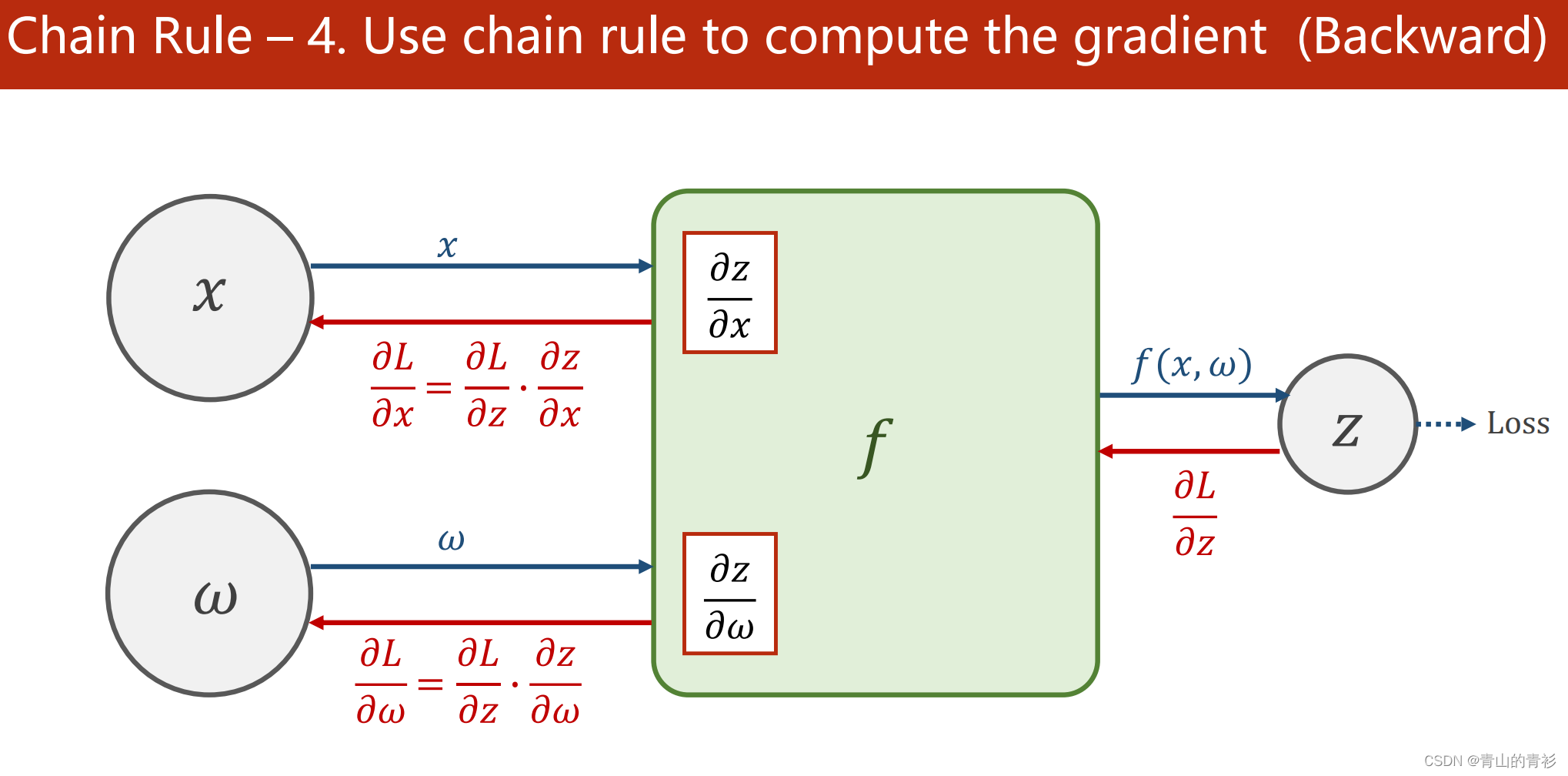
链式求导的规则,非常形象的图:

2.2 反向传播过程
1.构建计算图(前馈)
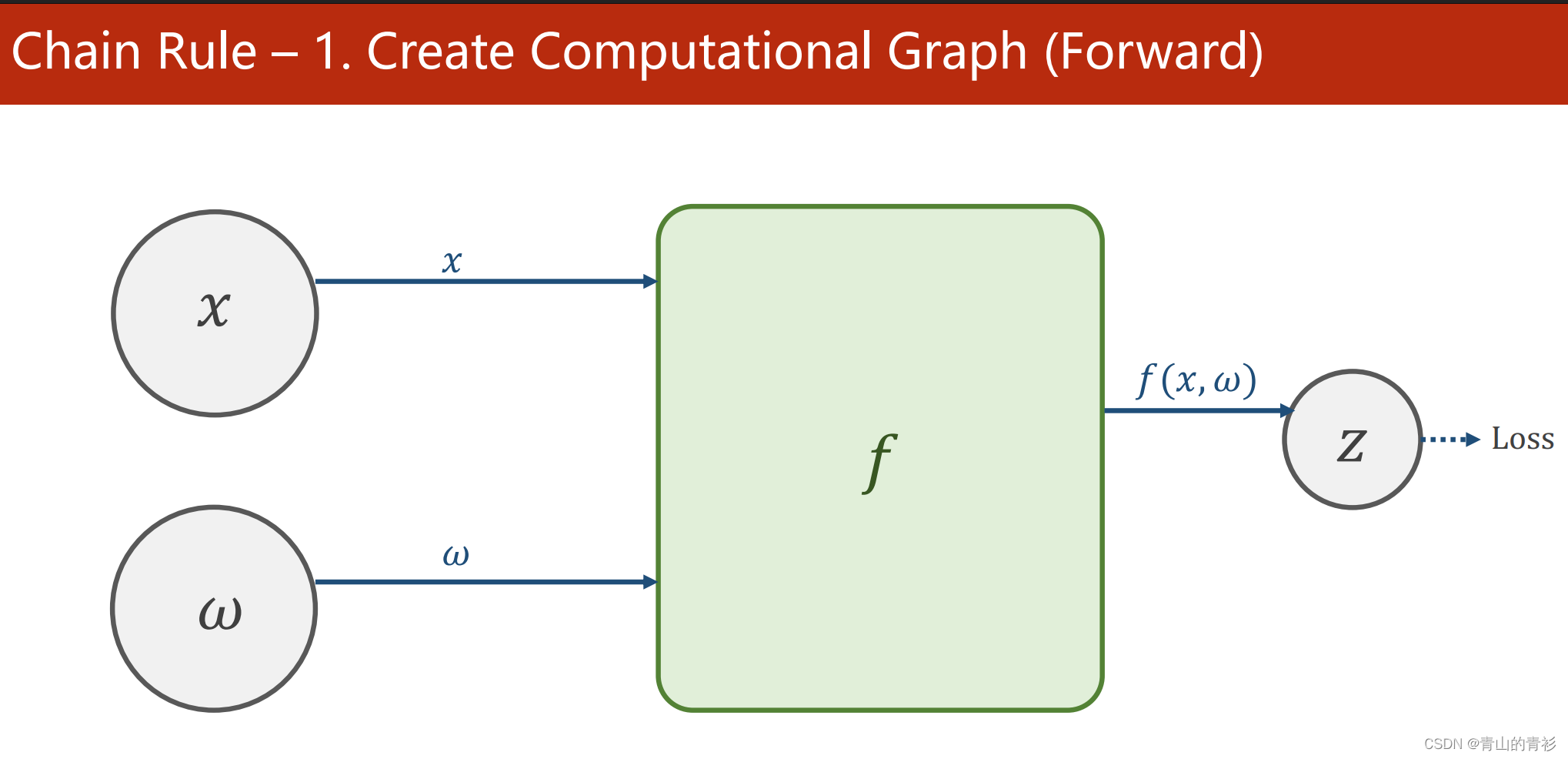
2. 求输出关于x和w的梯度

3. 损失L关于输出z的偏导

4. 运用链式求导法则,求L关于x和w的偏导(反馈)
一个简单线性模型(仿射模型)的前馈+反馈过程
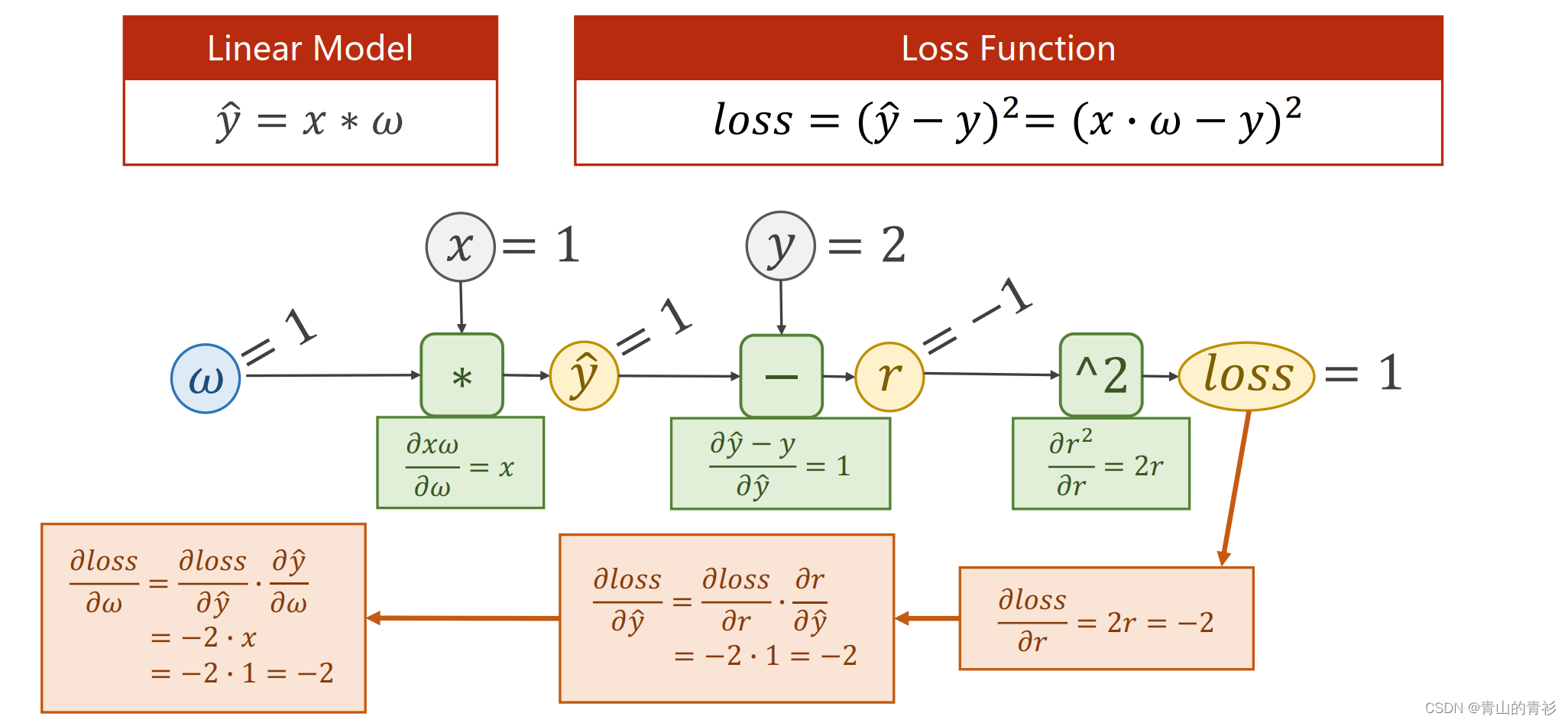
3.Pytorch中前馈和反馈的计算
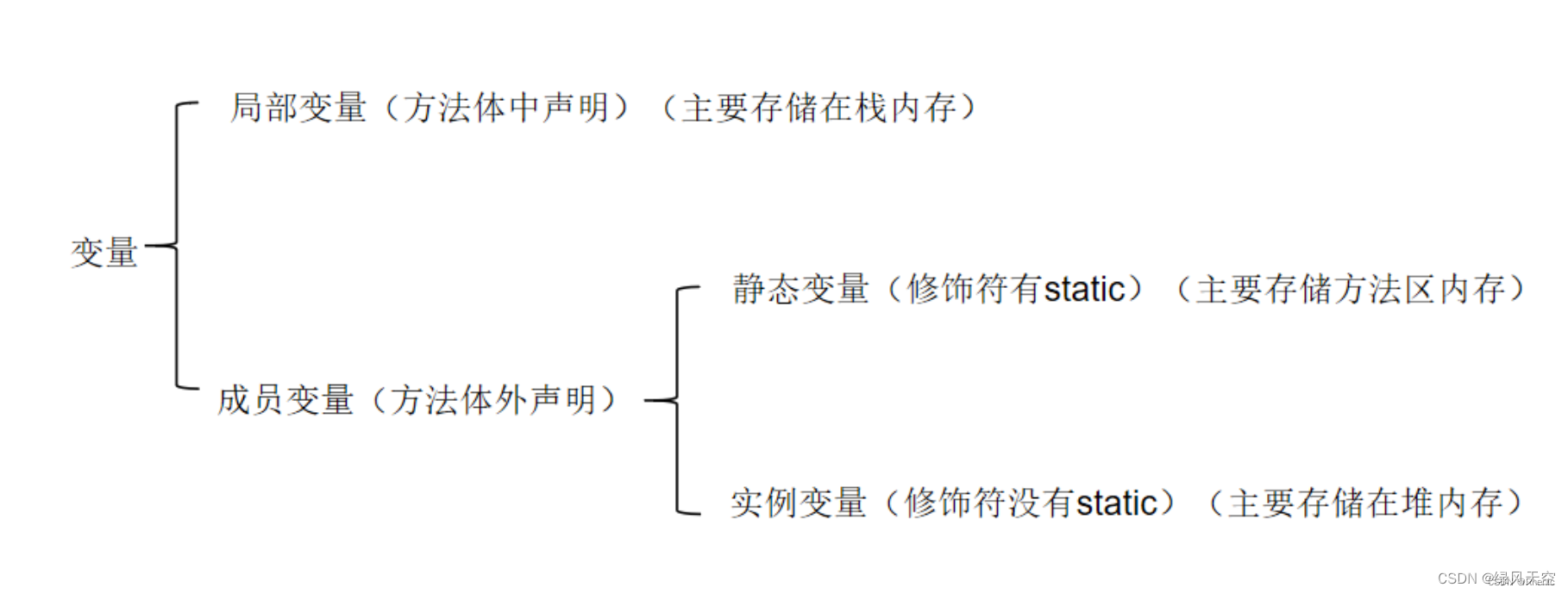
3.1 Tensor
参考博客
Tensor本身是一个类,里面包含两个比较重要的成员data(比如权重值)和grad(损失函数对权重的导数)
3.2 代码演示
import torch
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.Tensor([1.0])
w.requires_grad = True
def forward(x): # 前馈过程
return x * w # 因为w是tensor,因此x会自动类型转换变成tensor,输出的结果也变为tensor
def loss(x, y): # 损失函数
y_pred = forward(x)
return (y_pred - y) ** 2
loss_list = []
epoch_list = []
print("predict(before training)",4, forward(4).item()) # 因为数值是一维标量,所以可以直接用item取,不是标量(如向量,矩阵)得用data
for epoch in range(100):
for x, y in zip(x_data, y_data):
l = loss(x, y) # 前馈:前馈并计算损失函数
l.backward() # 反馈:张量自带的成员函数,会自动反向传播算梯度,把计算连路上所有需要的梯度都求出来,算完会释放这个计算图,每次都会创建新的计算图
print('\tgrad:', x, y, w.grad.item())
w.data = w.data - 0.03 * w.grad.data # 更新:.data得到的也是张量,但是只是数值改变的运算。不取data会构建计算图,占用内存
w.grad.data.zero_() # 把权重的梯度数据清零,不然后面几轮会累加计算
epoch_list.append(epoch)
loss_list.append(l.item())
print("progress:", epoch, l.item())
print("predict(after training)", 4, forward(4).item())
plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
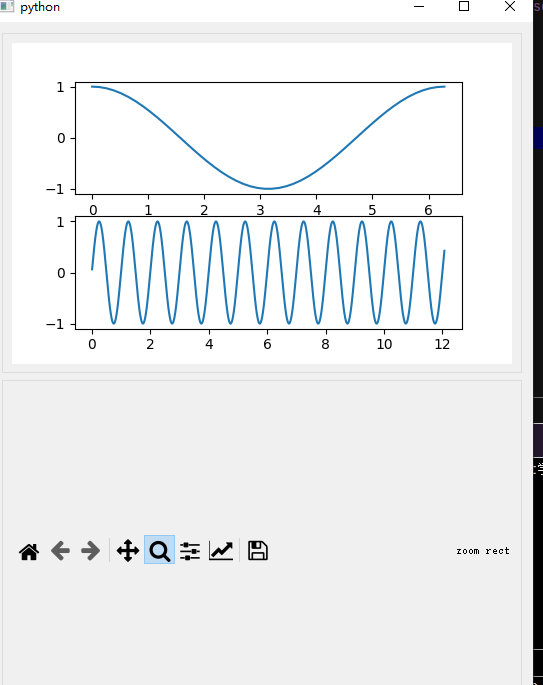
plt.show()
得到的图像如下: