1. 题目

泰波那契序列 Tn 定义如下： 

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2

给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

2. 示例

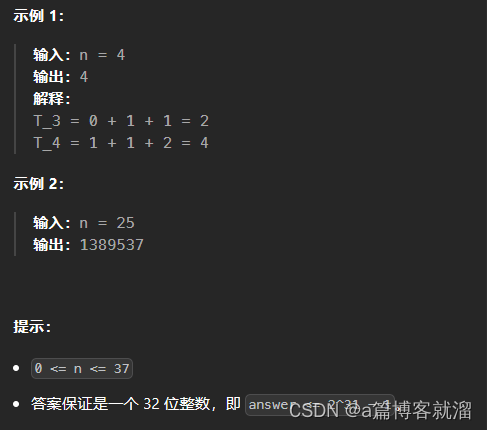
3. 分析

1. 状态表示：dp[i]表示：第i个泰波那契数的值

2. 状态转移方程：题目已经给了，为 Tn+3 = Tn + Tn+1 + Tn+2，修改一下为：dp[i] = dp[i-1] + dp[i-2] + dp[i-3]

3. 初始化：题目也已经给了，为 T0 = 0, T1 = 1, T2 = 1，修改一下为：dp[0] = 0,  dp[1] = d[2] = 1

4.填表顺序：填写一个状态时，需知道表里前三个的状态，所以根据方程可知填dp表的顺序就为 从左至右

---

class Solution {
public:
    int tribonacci(int n) {
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;

        vector<int> dp(n+1);
        dp[0] = 0, dp[1] = dp[2] = 1;
        for(int i = 3; i <= n; i++)
            dp[i] = dp[i-1]+dp[i-2]+dp[i-3];
        return dp[n];
    }
}

我们可以优化一下：我们不难发现对于dp[i]的值，我们只需用到前三个的值就可以了，并不需要前三个之前的值。例如dp[6]=dp[5]+dp[4]+dp[3]，我们求dp[6]时是不需要用到dp[0]、dp[1]、dp[2]的，即dp[0]、dp[1]、dp[2]对于dp[6]是可以舍弃掉的。

结论：求某个状态时，仅需要有效的状态，对于不用的就可以舍弃掉。

我们就可以使用滚动数组进行优化。我们使用abcd四个变量分别进行赋值 a = 0, b = 1, c = 1, d = 0，然后在这个数组内一步一步走就可以了。

怎么走呢？交换彼此的值就行，有两种交换选项：

1. 从左往右走： a = b, b = c, c = d 为正确走法
2. 从右往左走：c = d, b = c, a = b
   错误走法：c = d再b = c后，b的值就为d了，而不是还没交换前的c了。

class Solution {
public:
    int tribonacci(int n) {
        if(n == 0) return 0;
        if(n == 1 || n == 2) return 1;

        // 空间优化
        int a = 0, b = 1, c = 1, d = 0;
        for(int i = 3; i <= n; i++)
        {
            d = a + b + c;
            a = b; b = c; c = d;
        }
        return d;
    }
};