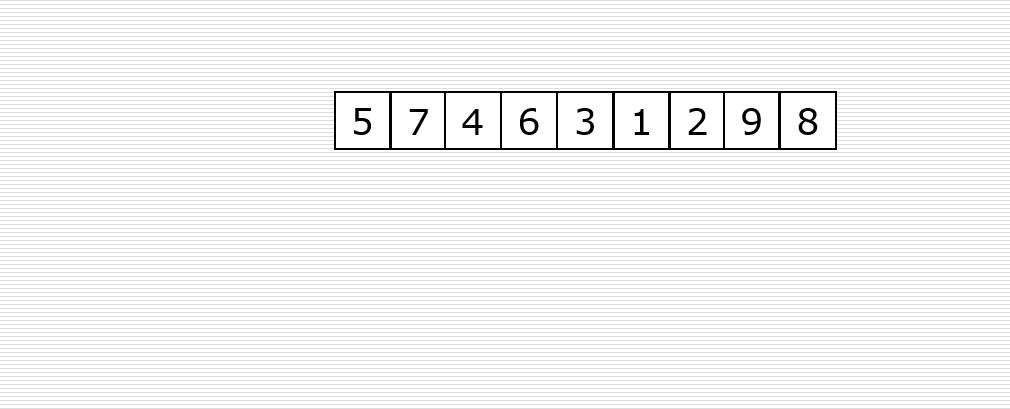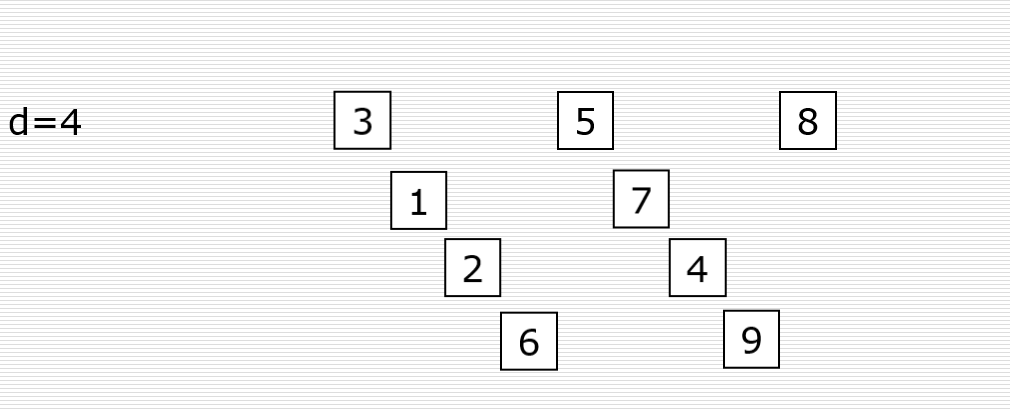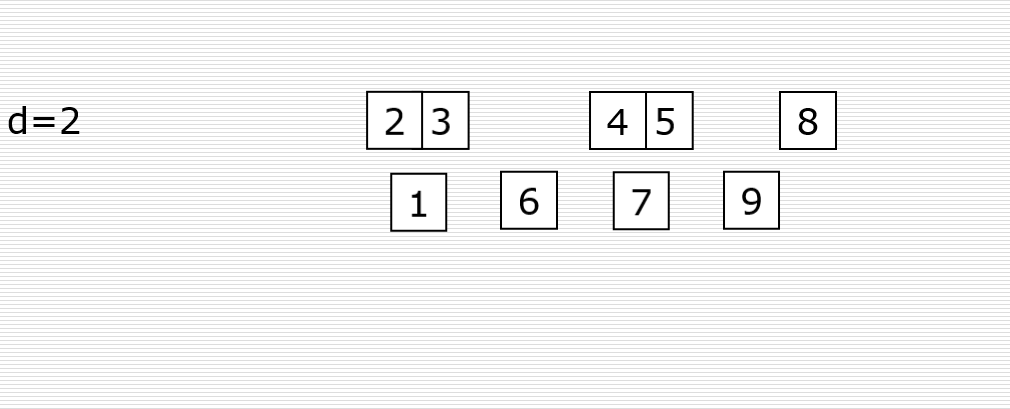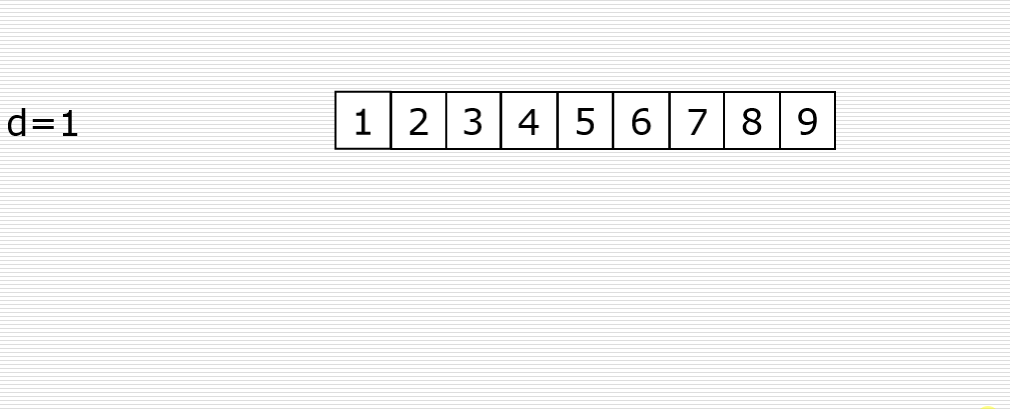
目录
- 数据依赖
- 范式
- 第一范式1NF
- 第二范式2NF
- 第三范式3NF
- BC范式
- 数据依赖的公理系统
- 闭包
- 最小依赖集
- 候选码
- 设计
- 需求分析
- 概念结构设计
- E-R图的概念模型
- E-R模型转换为关系模型(指出转换结果中每个关系模式的主码和外码)
- 逻辑结构设计
- 物理结构设计
- 数据库实施
- 数据库运行和维护
数据依赖
基础
FD(functional dependency),数据库系统函数依赖。
码
K为 R<U,F> 中属性或属性的组合
K(Full完全依赖)U, 则K为R的候选码 (特殊的超码)/ 超码
单个属性是码
全码: 整个属性组是码,称为全码
外码
码 用下划线标出
主属性: 包含在任何一个候选码中的属性
非主属性: 不包含在任何候选码中的属性
超码
如果属性集合X能够唯一确定Y,而且X的任何真子集都不能唯一确定Y,那么X就是关系R的超码。
举个例子,假设有一个关系模式R(ABCDE),如果属性集合{AB}能够唯一确定C,而且A和B的任何真子集都不能唯一确定C,那么{AB}就是R的一个超码。
确定FD
R(U,F) ,X,Y
R关系模式名,如学生表student
U 属性名的集合, X为U中一个属性区间, Y同样也是,如U={ sno, sname ,ssex} , X={sno,sname}
F 属性间依赖关系集
y=f(x) : x值确定, 则y值确定
数据库中:
x:决定因素 , y函数依赖x
sno 学号确定姓名, sname 姓名依赖于学号
平凡函数依赖
判断
x 完全决定于 y ,无需其他属性参与
y包含在x中
当一个属性集合X的函数依赖于属性集合Y时,如果Y是X的子集,那么这个函数依赖被称为平凡函数依赖。简单来说,平凡函数依赖指的是一组属性完全决定了另一组属性,没有任何其他附加条件。
举例说明:假设有一个关系模型R,属性集合为{A, B, C},其中A是关系模型中的候选键。如果函数依赖A -> B 存在于R中,那么这是一个平凡函数依赖。因为A本身已经能够完全决定B的值,没有其他附加条件。
非平凡函数依赖
判断
x 部分决定于 yz , 需要其他属性参与才可完全决定yz
yz 不包含在x中
确定候选键:首先需要识别出关系中的所有候选键。
检查函数依赖:查看关系中的所有函数依赖,特别是非平凡函数依赖。
验证左侧蕴含:对于每一个非平凡函数依赖,检查其左侧是否可以独立地确定右侧的属性。
验证左侧为候选键的一部分:对于每一个非平凡函数依赖,检查其左侧是否至少是候选键的一部分,或者能够推出候选键。
非平凡函数依赖:当一个属性集合X的函数依赖于属性集合Y时,如果Y不是X的子集,那么这个函数依赖被称为非平凡函数依赖。简单来说,非平凡函数依赖指的是一组属性可以部分决定另一组属性,但不能完全决定,需要其他属性的参与。
举例说明:假设有一个关系模型R,属性集合为{A, B, C, D},其中A是关系模型中的候选键。如果函数依赖A -> BCD 存在于R中,那么这是一个非平凡函数依赖。因为A本身无法完全决定B、C、D的值,还需要其他属性的参与。
非平凡, X,Y之间有包含关系
x 决定 y, y不包含x
如:(sno,cno) 决定 grade
函数依赖
完全函数依赖
ab---c, 但a 不能决定 c
(sno,cno) 完全函数依赖full 成绩grade
单独一个学号不能确定 成绩 grade
定义: X 决定Y, 且x'(x中的一个真子集) 不能决定 Y
举例: 通过AB能得出C,但是A, B单独得不出C,那么说C完全依赖于AB.
比如(学号,课名)->成绩,而单独的学号或者课名都不能确定成绩,这就叫完全函数依赖
总结: 只能由某个属性A或属性组决定另一个属性B,此外其他的所有属性都不可决定另一个属性B
部分函数依赖(2nf)
ab--c, 且a--c,b---c
(sno,cno) 部分函数依赖 系别sdept
y部分函数依赖 x, 则x必定是组合属性
x决定Y, Y不完全函数依赖于X
举例: 通过AB能得出C,通过A也能得出C,通过B也能得出C,那么说C部分依赖于AB。
比如(学号,课名) 决定 姓名,而单单的 学号 也可以决定姓名, 这样的依赖就叫部分函数依赖。
总结: 可以有多个属性决定 另一个属性B,
传递函数依赖(3NF)
x--y (y不能决定x) , 且 y ---z, 则: x---z
x 确定 y, y确定 z , 且 y不能确定x , 则 x 传递函数 z 或
通过A得到B,通过B得到C,但是C得不到B,B得不到A,那么成C传递依赖于A
比如学号->系名,系名->系主任,并且(系名不能决定学号),所以系主任传递函数依赖学号
范式
对关系模式判定的条件, 关系必须满足一定的要求
范式间的关系
5NF最为严格(关系模式好), 1NF最宽松(关系模式不好)
关系的规范化
规范化: 一个低一级范式的关系模式,通过模式分解可以转换为若干个高一级范式的关系模式的集合,这种过程就叫规范化
低范式到高范式的分解
取其精华,弃其糟粕
第一范式1NF
判断:
属性不可再分,原子性; 确保每个单元格中只有一个值
例如
属性电话号码, 若包含多个电话号码的字段,那么这个表就不符合第一范式
只能是一个电话号码 对应 一个 记录
如Excel表,单元格合并拆分, 不符合1NF
第二范式2NF
判断
非主键列必须完全依赖于整个主键 ,不存在部分函数依赖 ;
ab---c ; a / b 不能决定c
满足2nf的条件
每一个非主属性都完全函数依赖于R的码
1nf 到2nf :
1NF 到 2NF: 消除非主属性对码的部分函数依赖
slc(sno,cno,sdept,sloc住处,grade) 关系模式
部分/完全 函数依赖
full: (sno,cno) f grade
part:
sno- sdepte, (sno,cno) p sdept (不符合2nf)
sno- sloc, (sno,cno) p sloc
分解到2nf
投影分解法:
完全函数依赖 / 部分函数依赖单独拉出来
使其规范到2nf
完全函数依赖的,单独投影出来
sc(sno,cno,grade)
部分函数依赖,拉出来:
sl(sdepte,sloc), 通过sno建立联系,最终为 : sl(sno, sdepte,sloc)
存在的问题:
IS系学生全部毕业: sdepte,sno,sloc全部删除,异常
第三范式3NF
判断条件
所有非主属性都不传递依赖于主属性
a-b b- c ; 但a不能决定c
传递函数依赖
2NF 到 3NF : 消除非主属性对码的传递函数依赖
若R 属于 3NF,则每一个非主属性既不部分依赖于码也不传递依赖于码
不存在非主属性对主属性的传递函数依赖
sl(sno,sdept,sloc) (不属于3NF)
例如:2NF sl(sno, sdept, sloc)
函数依赖为: sno - sdept, sdepte不- sno, sdept- sloc , 可得: sno 传递- sloc ,存在非主属性对码的传递函数依赖
分解到3nf:
投影分解使其消除传递函数依赖:
SD(sno,sdepte) ,码为sno
DL(sdept,sloc) , 码为 sdepte
此时不存在传递依赖
BC范式
判断
不存在 非平凡(部分函数) 依赖
每一个函数依赖的左边都包含了关系的候选键
3NF 到 BCNF 消除主属性对码的部分和传递函数依赖
特: BC范式属于3NF, 其他不是
为改善的第三范式
stj(s,t,j) : s学生,t教师,j课程
自动满足3NF,但也有插入删除异常
第四范式
第五范式
数据依赖的公理系统
逻辑蕴含
armstrong 公理系统
自反律: ab-- a ; ab ; b (自身)
增广律: x-y ; 则 xz-yz (同乘以z) ; (扩展)
传递律: x-y ,y-z , 则 x-z (传递)
举例(根据自反律与增广律得到: ab 决定-c, 则a-b,b-c )
推理规则
合并规则: x-y,x-z , 有 x-yz (合并到右,左不变)
分解规则: x-yz, 得 x-y, x-z ( 右边分解,左不变)
伪传递规则: x-y, wy-z , 有xw-z (消除掉了Y )

复合律
过x- y 和 w-z 在r 上成立, 则xw-yz 在r上也成立(左边乘右边)
闭包
总结:
求属性BD的闭包,求该属性F函数依赖的全体, 记为(BD)F+
计算方法:
在函数依赖集合中,在左边(决定属性)中查找仅包含B/D/BD的式子
设x(0), 找到相对应的右边的属性, 并合并左边的属性一起作为下次循环的决定属性; 循环重复, 最终得到的属性不可重复即可
定义: 在关系模式R<U,F>中为F所逻辑蕴含的函数依赖的全体叫作F的闭包(closure),记为F+
作用:
计算过程 类似 for循环
求ab属性的闭包,记为: (ab)f+
设 x(0)= ab
求a,b, 所有组合的元素的式子
a,b,ab
注意: 左边的包含ab,不能有其他的
ab-c, b-d
把右边的属性并到原有的x中: x(0) =abcd
循环
x(1)= abcd
求a,b,c,d所有组合的元素的式子
c-e, ac-b
继续并 得到: x(1) =abcde
当x(1)=U时, 结束运算, 得到(ab) f+ 闭包
最小依赖集
步骤:
1. 分解右部属性,使之称为单个属性
2. 消除冗余函数依赖 (通过求各自B包, 假设该依赖冗余, 此时依赖集中去除该依赖,求b包; 若推不出右边属性或求出的B包中没有右边的属性,则保留; 反之,则删除)
3. 接上步, 删除后得到此时的F; 消除此时剩下的左边为双属性, 删除左边的一个属性,对另一个属性求B包. 若, 推不出右边属性 或求出的B包中没有右边的属性,则保留; 反之,则删除 ( 删除后则其中一个属性就被删除了, 但保留的属性还在 ,就变为单属性了)
注意: 若进行到第3步, 则需要重新执行第 2步
要求:
这时需要分解
最后 保留的依赖集, 不能由其他函数推导出
最小依赖集求解的方法与步骤:
(1)应用分解规则,使F中每一个依赖的右部属性单一化
(②)去掉多余的依赖。
(③)去掉各依赖左部多余的属性。
计算:
f中的最小依赖集
f{ a-bc , b-c, a-b, ab-c, }
1. 找到右边双属性的
a-bc ,分解得到:
a-b, a-c
去重复, 两个a-b
2. 因为 a-b,b-c, 推导出a-c, 则a-c可删除
3. ab-c, 由 a-b,b-c推出, ab-c可删除
候选码
候选码计算方法:
在函数依赖F中
1 找到函数依赖集的左边L / 右边R / 既在左边又在右边LR 出现的 属性, 一 一分组列出
2 计算仅在函数依赖左边出现的属性的闭包+ , 若等于U中全部的属性,则是候选码; 结束
3 不等于U中全部属性则需要考虑 既在左边又在右边LR出现的 属性:
在LR中取一个属性A,求(A)F+ ,若它包含了U中全部属性,则为候选码成员;
在LR中取出另一个属性 循环进行这一过程,直到试完所有LR中的属性
4 然后在LR中依次取剩余属性中两个属性、三个属性....., 求它们的属性集的闭包,直到其R的全部属性被取完 结束
准则1:如果某个属性A只在F中各个函数依赖的箭头左边出现,则A必是候选码中的属性。
准则2:如果某个属性A只在F中各个函数依赖的箭头右边出现,则A必不是候选码中的属性。
准则3:如果某个属性A既在F中某个函数依赖的箭头右边出现,又在其他函数依赖的箭头左边也出现,则A有可能是候选码中的属性。
准则4:如果某个属性A不在F的各个函数依赖中出现,则A必是候选码中的属性
根据这些准则,确定候选码的步骤是:
根据准则1,确定码中必有的属性(设为M)
先根据准则2,把不在F的各个函数依赖中出现的属性去掉;
根据准测3,去掉码中肯定没有的属性集;
确定余下的属性集(设为W)
从属性集M开始,令K=M,如果K+=U,K就是候选码。否则从
W中选择属性加入到K中,直至K+=U,K就是候选码。
注意可能有多个候选码。

模式分解
关系模式R(U,F)中,F是最小函数依赖集。
准则1:如果属性A只在F中各个函数依赖的左部出现,则A必是码中的属性;
准则2:如果属性A不在F中各个函数依赖中出现,则A必是码中的属性;
准则3:如果属性A只在F中各个函数依赖的右部出现,则A必不是码中的属性。
属性只在左边出现, 为码中属性,主属性
属性只在右边出现, 非主属性
根据这些准则,确定候选码的步骤是:
1. 先根据准则2,把不在F的各个函数依赖中出现的属性去掉;
2. 根据准则1,确定码中必有的属性(设为M)。
3. 根据准则3,去掉码中肯定没有的属性集;
4.确定余下的属性集(设为W)。
5.从属性集M开始,令K=M,如果K+=U,K就是候选码。否则从W中选择属性加入到K中,直至K+=U,K就是候选码。
6. 注意可能有多个候选码·
kf+=U, k就是候选码
可能有多个候选码
计算步骤:
fmin{ b-d, b-g, c-d, c-a, ce-b}
只在左边出现的 ce
只在右边出先的: 啊,的,g
余下属性: b
r候选码可能是:
例题1(码) :
 解:
解:

例题2 (闭包/最小依赖集):
 解:
解:
例题3(最小依赖集):

例题4(最小依赖集/候选码):
 解:
解:



 闭包:
闭包:

习题:




设计
需求分析
调研/调查
概念结构设计
设计E-R图
长方形: 实体
菱形: 联系名
椭圆: 属性(不可再分 , 不可与其他实体集 有联系 )
属性冲突( 学号 与 学生编号, 同一个属性,不同人命名不同 )
无向边: -------
确定: 实体 / 属性 / 联系( 供应商 供应 零件 )
消除冲突冗余
联系:
m: n
问题
E-R图的概念模型
步骤
确定实体
画出该实体对应的属性,中间属性 及键(下划线标出)
确定各个实体对应的 联系 m:n
确定中间属性的联系
例题:
某企业集团有若干工厂,每个工厂生产多种产品,且每一种产品可以在多个工厂生产,每个工厂按照固定的计划数量生产产品;每个工厂聘用多名职工,且每名职工只能在一个工厂工作,工厂聘用职工有聘期和工资。工厂的属性有工厂编号、厂名、地址,产品的属性有产品编号、产品名、规格,职工的属性有职工号、姓名。
(1)根据上述语义画出E-R图;
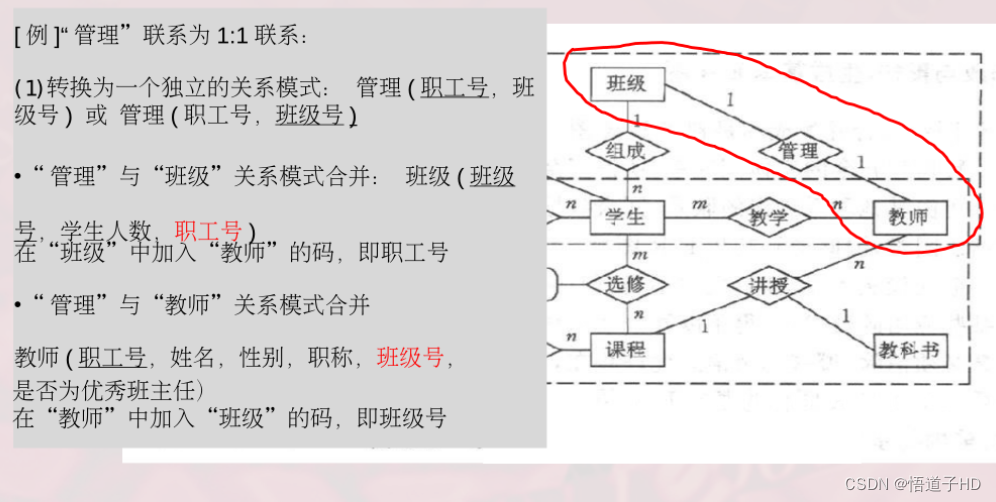
(2)将该E-R模型转换为关系模型,指出转换结果中每个关系模式的主码和外码 (要求:1:1和1:n的联系进行合并)
E-R模型转换为关系模型(指出转换结果中每个关系模式的主码和外码)
(1)实体到关系模式的转换
1 实体型的转换:一个实体型转换为一个关系模式(带括号的形式)
根据联系间的某个实体 / 联系进行转换 ,转换为实体( 主码,属性 ... 另一个属性的外码 ) ; 另一个实体名( 主码, 属性....... ) / 联系( 实体主码, 另一个实体主码)
注意:m:n联系中, 对联系中的外键为 两个实体主码的组合
关系模式的属性:实体的属性
关系模式的码:实体的码
转换为
学生(学号,姓名,出生日期,所在系,年级,平均成绩)
1:1联系

1:n联系


m:n联系

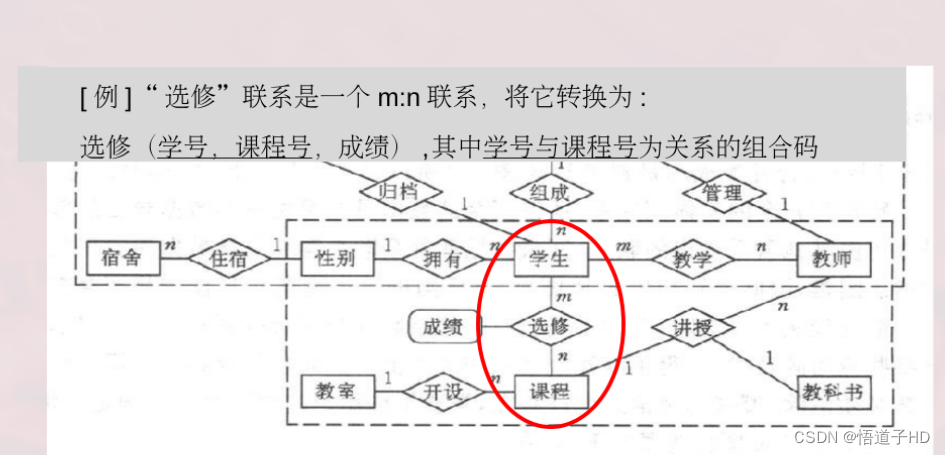
(2)联系到关系模式的转换
逻辑结构设计
步骤:
将实体转换为关系模式
将联系转换为关系模式
去掉冗余
标出主外键( 主码下划线, 文字注明外码)
数据模型
关系/非关系
1:1 转换 关系模式
添加码到另一个关系的 实体中
1:n
添加(合并)码 到 n关系的 实体中
特殊: 职工( ........ 领导 )
m:n
取中
将联系做成一个独立的关系模式, 属性来自 m 和 n 中 ( 联合作为主码, 单独分别作为外码) 和 本身的属性
物理结构设计
放在哪个分区( 频繁/ 非频繁) , 索引
数据库实施
创建.....建表.....
组织数据入库
试运行: 如选课系统, 三年左右
数据库运行和维护
售后: 性能检测/ 恢复.......
—————————————————————
以上就是今日博客的全部内容了
创作不易,若对您有帮助,可否点赞、关注一二呢,感谢支持.