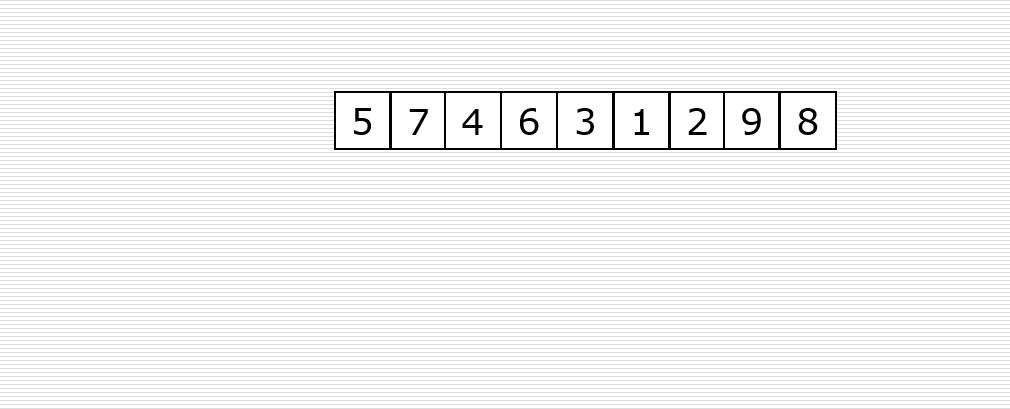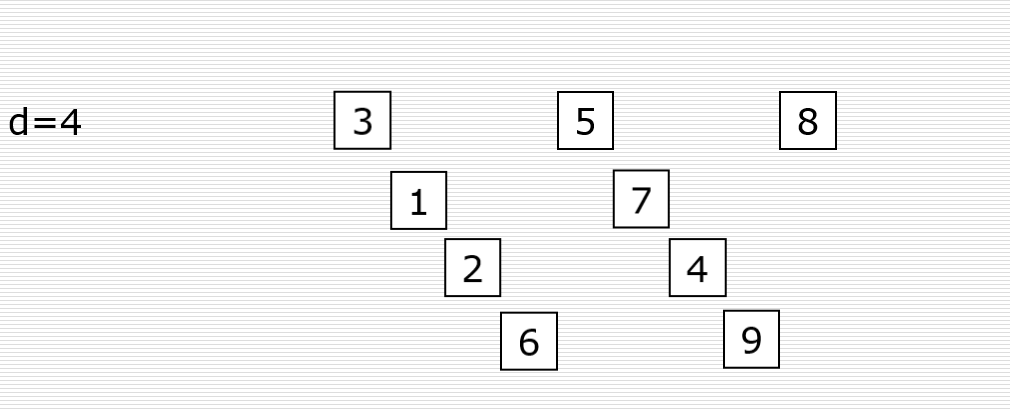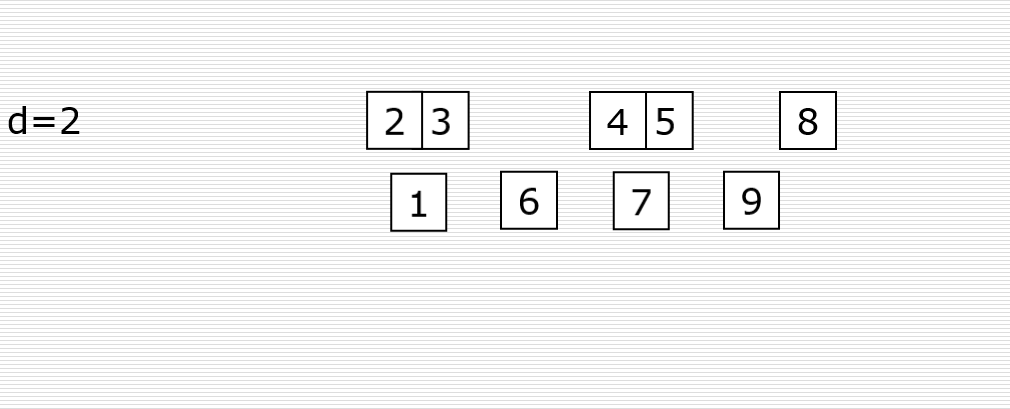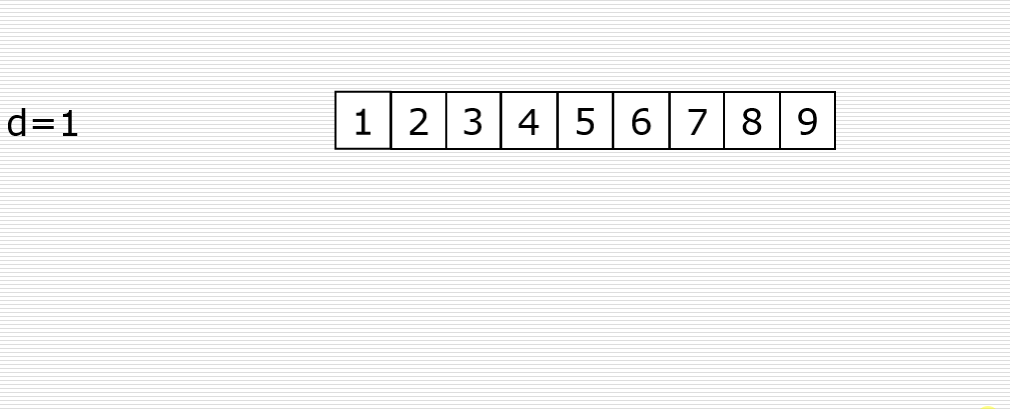
5.3 栈
1.STL-stack
基本代码
#include <bits/stdc++.h>
using namespace std;
int main() {
stack<int> myStack; // 定义一个整型栈
// 输出栈的初始大小
cout << "The size of myStack: " << myStack.size() << endl;
// 将0到9的整数压入栈中
for (int i = 0; i < 10; ++i) {
myStack.push(i);
}
// 输出栈顶元素
cout << "The top of myStack: " << myStack.top() << endl;
// 输出栈的大小
cout << "The size of myStack: " << myStack.size() << endl;
int sum = 0; // 定义一个变量用于累加栈中元素的值
// 当栈不为空时,循环执行以下操作
while (!myStack.empty()) {
// 将栈顶元素的值加到sum中
sum += myStack.top();
// 弹出栈顶元素
myStack.pop();
}
// 输出累加结果
cout << "Sum: " << sum << endl;
// 检查栈是否为空,并输出信息
if (myStack.empty()) {
cout << "myStack is empty" << endl;
}
return 0;
}2.栈的应用
例:零复杂度转置
题目描述
你会得到一个整数序列。序列的零复杂度转置与此序列相反。您的任务是编写一个程序来打印给定序列的零复杂性转置。
输入描述:对于每种情况,输入文件的第一行都包含序列的一个整数 n 长度(0 < n ≤ 10 000)。第二行包含 n 个整数数字-a1、a2、...、an (-1 000 000 000 000 000 ≤ ai ≤ 1 000 000 000 000 000)。
输出描述:对于每种情况,在输出文件的第一行上以相反的顺序打印序列。
思路提示:看到了转置就要想到用栈因为它后进先出的特性;注意这道题的数据比较大,所以需要用到long long的数据类型。以及longlong的scanf输入是%lld
代码表示
#include <bits/stdc++.h>
using namespace std;
stack<long long> sequence; // 定义一个长整型栈
int main() {
int n;
// 循环读取输入直到文件结束
while (scanf("%d", &n) != EOF) {
// 循环n次
while (n--) {
long long number;
// 读取一个长整型数 long long类型
scanf("%lld", &number);
// 将数压入栈中
sequence.push(number);
}
// 当栈不为空时,循环执行以下操作
while (!sequence.empty()) {
// 输出栈顶元素
printf("%lld ", sequence.top());
// 弹出栈顶元素
sequence.pop();
}
printf("\n");
}
return 0;
}例:括号匹配问题
题目描述:
代码表示:
#include <bits/stdc++.h>
using namespace std;
int main() {
char buf[200];
//从标准输入中读取一行文本并将其存储在buf中
while (fgets(buf, 200, stdin) != NULL) {
// fgets配合while实现不确定数量的多行读取
string str = buf;
str.pop_back(); //移除字符串str的最后一个字符
stack<unsigned> indexStack; // 存储左圆括号
string res; // 保存输出的结构
for (unsigned i = 0; i < str.size(); ++i) {//遍历字符串str
if (str[i] == '(') {
indexStack.push(i);
}
else if (str[i] == ')') {
if (indexStack.empty()) {
res.push_back('?');
}
else {
res.push_back(' ');
res[indexStack.top()] = ' ';
indexStack.pop();
}
} else {
res.push_back(' ');
}
}
printf("%s\n%s\n", str.c_str(), res.c_str());
}
return 0;
}心得体会:
1、res.push_back(' '):在结果字符串res中添加一个空格字符,用于分隔不匹配的右圆括号和匹配的左圆括号。
2、res[indexStack.top()] = ' ':将栈顶元素对应的左圆括号位置设为空格,表示该左圆括号已经找到了匹配的右圆括号。
3、indexStack.pop():从栈indexStack中弹出栈顶元素,表示匹配的左圆括号已经处理完毕。
4、str.c_str()和res.c_str()是C++字符串类(std::string)提供的成员函数,用于返回字符串的C风格字符数组表示。
str.c_str():返回一个指向以null结尾的字符数组,其中包含str字符串的内容。这个字符数组可以被传递给需要以C风格字符串作为参数的函数或输出流。res.c_str():返回一个指向以null结尾的字符数组,其中包含res字符串的内容。
在给定的上下文中,printf函数是一个C语言的输出函数,它需要以C风格的字符串作为参数。因此,str.c_str()和res.c_str()被用作printf函数的参数,以便将字符串内容传递给printf函数进行格式化输出。
5、fgets是一个C语言的函数,用于从输入流中读取一行文本并将其存储到指定的字符数组中。
函数原型如下:
char* fgets(char* str, int num, FILE* stream);
参数说明:
str:指向字符数组的指针,用于存储读取的文本。num:要读取的字符的最大数量(包括空字符)。stream:要从中读取文本的输入流。通常使用stdin表示标准输入流。
PS:fgets(buf, 200, stdin)的作用是从标准输入中读取一行文本,并将其存储到字符数组buf中,最多读取200个字符(包括换行符)。
22年蓝桥杯题
22年砍竹子
题目描述
这天,小明在砍竹子,他面前有 n 棵竹子排成一排,一开始第 i 棵竹子的高度为hi,他觉得一棵一棵砍太慢了,决定使用魔法来砍竹子。魔法可以对连续的一段相同高度的竹子使用,假设这一段竹子的高度为 H,那么使用一次魔法可以把这一段竹子的高度都变为![]() 其中⌊x⌋ 表示对 x 向下取整。小明想知道他最少使用多少次魔法可以让所有的竹子的高度都变为 1。
其中⌊x⌋ 表示对 x 向下取整。小明想知道他最少使用多少次魔法可以让所有的竹子的高度都变为 1。
输入格式
第一行为一个正整数 n,表示竹子的棵数。
第二行共 n 个空格分开的正整数 hi,表示每棵竹子的高度。
输出格式
一个整数表示答案

代码表示
#include <bits/stdc++.h>
using namespace std;
typedef long long LL; //将long long类型重命名为 LL
const int M=200010,N=10; //定义常量 M行和 N列
LL arr[M][N]; //定义二维数组存储每个竹子经过魔法变化后的高度
int main() {
int n; // 声明变量 n
cin >> n; // 从标准输入读取 n 的值
//sta(用于存储每个竹子高度段的栈)、top(表示当前竹子高度段的数量)
//mx(记录所有竹子高度段的最大数量)、cnt(记录所有竹子经过魔法变化的总次数)
LL sta[10], top=0, mx=0, cnt=0;
for (int i = 0; i < n; i++) {
top = 0;
LL p;
cin >> p; // 从标准输入读取 p 的值
while (p > 1) {
sta[top++] = p; //将当前竹子的高度p存入栈sta中,并将top加1
p = sqrt(p/2 + 1);
}
mx = max(mx, top); // 更新 mx 的值为 mx 和 top 中的较大值,竹子高度段的最大数量
cnt += top; // 将 top 的值累加到 cnt 上
//循环遍历当前竹子的高度段,同时使用两个变量j和k,k从高度段的末尾开始,j从0开始
for (int j = 0, k = top - 1; k >= 0; j++, k--) {
arr[i][j] = sta[k]; // 将 sta数组中的元素逆序存入 arr[i] 数组中
}
}
for (int i = 0; i < mx; i++) {
for (int j = 1; j < n; j++) {
if (arr[j][i] == arr[j-1][i] && arr[j-1][i]) {
cnt--; //不需要额外的魔法次数
}
}
cout << cnt << endl; // 将 cnt 的值输出到标准输出
return 0;
}心得体会
代码的主要逻辑如下:
1、从输入中读取竹子的数量n。
2、定义一个二维数组arr,用于存储每个竹子经过魔法变化后的高度。
3、遍历每个竹子,对于每个竹子进行如下操作:
1)初始化一个变量top为0,表示当前竹子经过魔法变化后的高度段数。
2)读取当前竹子的初始高度p。
3)通过一个循环将当前竹子的高度p不断变化,直到变为1。在每次循环中,将当前高度p存入一个栈sta中,并将top加1。同时,更新高度p为⌊ sqrt(⌊p/2⌋ + 1)⌋,即将当前高度段的竹子高度经过魔法变化后的高度。
4)记录当前竹子经过魔法变化后的高度段数top的最大值mx,以及所有竹子经过魔法变化的总次数cnt。
5)将栈sta中的元素逆序存入二维数组arr中,表示当前竹子的高度段经过魔法变化后的高度。
6)通过两个嵌套循环遍历每个竹子的每个高度段。如果当前竹子的高度段与上一个竹子的相同且不为0,则将cnt减1,表示这个高度段不需要额外的魔法次数。
7)输出变化的总次数cnt,即为最少需要使用的魔法次数,以使所有竹子的高度都变为1
试题 A:九进制转十进制
【问题描述】
九进制正整数 2022转换成十进制等于多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
1478(进制转换就手算吧哈)
补充进制转换手算知识
1、十进制转二进制(十进制转换为X进制:给出的十进制数 ÷X;余数从下往上读得到X进制数)
除2取余倒序输出:十进制转二进制的转换原理:除以2,反向取余数,直到商为0终止。
eg: 9(10)=1001(2)

除8取余倒序输出:转换原理:除以8,反向取余数,直到商为0终止。
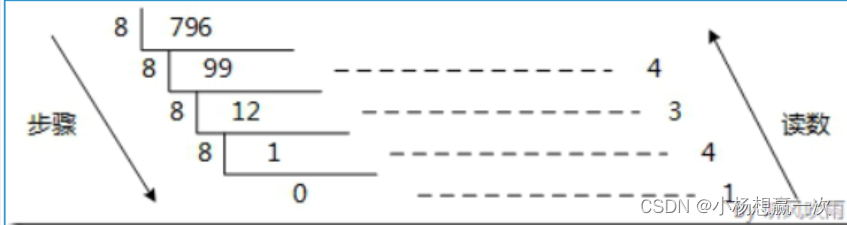
2、X进制转换为十进制(第一位系数*X^0+第二位系数*X^1.......)

小数:

3、二进制转换为八进制和十六进制(分别写出二进制后 三合一 和 四合一)


4、八进制、十六进制转换成二进制(八进制数的一位是二进制数的三位,十六进制数的一位是二进制数的四位)

5、八进制与十六进制之间的转换两者之间的转换
可以借助十进制或者二进制完成,可以先将八进制转换成十进制或二进制,再转换成十六进制
试题 B:顺子日期
【问题描述】
小明特别喜欢顺子。顺子指的就是连续的三个数字:123、456 等。顺子日期指的就是在日期的 уyyymmdd 表示法中,存在任意连续的三位数是一个顺子的日期。例如 20220123 就是一个顺子日期,因为它出现了一个顺子:123; 而 20221023 则不是一个顺子日期,它一个顺子也没有。小明想知道在整个 2022 年份中,一共有多少个顺子日期。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
14
找1 2 3和0 1 2组合的日期,注意与年无关了因为题目要求顺子也就是指从小到大了。
01.23;11.23;12.30;12.31;
01.21;01.22;01.23;01.24;01.25;01.26;01.27;01.28;01.29;
10.12;
经验:会做的手算题,一定要认真仔细拿到分,这道题一开始就不仔细导致考虑的不周到。