---

1.背景

2019年，Heidari 等人受到哈里斯鹰捕食行为启发，提出了哈里斯鹰算法(Harris Hawk Optimization, HHO)。

2.算法原理

2.1算法思想

根据哈里斯鹰特性，HHO分为探索-过渡-开发三个阶段。

2.2算法过程

探索：
哈里斯鹰以其强大的视力追踪和检测猎物，但有时猎物不易察觉。它们会在沙漠地区等待、观察和监视，可能需要几个小时才能发现猎物。哈里斯鹰会随机停歇在某些位置，并等待检测猎物，使用两种策略：当$q<0.5$时根据其他家庭成员和猎物的位置进行停歇；当$q\ge 0.5$时停歇在随机的高树上。
$$X(t+1)=\{\begin{array}{ll}{X}_{rand}(t)-r_1|X_{rand}(t)-2r_{2}X(t)|& q\ge 0.5\\ (X_{rabbit}(t)-X_m(t))-r_3(LB+r_4(UB-LB))& q<0.5\end{array}$$
其中，$X_{rand}(t),X_{rabbit}(t),X_m(t)$分别为随机个体位置，猎物位置（当前适应度最优）和群体平均位置。
过渡：
过渡阶段根据猎物的逃逸能量之间切换不同的开发利用行为。在猎物逃逸行为期间，猎物的能量会大幅下降，表述为：
$$E=2E_0(1-\frac{t}{T})$$
在迭代过程中，动态逃逸能量$E$呈下降趋势。当逃逸能量$E\ge 1$时，哈里斯鹰会搜索不同的区域中的猎物（全局探索）；当$E<1$时，哈里斯鹰搜索猎物周围（局部探索）。
开发：
开发阶段较为复杂，文章中提出了四种捕食策略。首先，根据猎物是否逃脱这里由参数$r$判定；哈里斯鹰采取软、硬进攻方式这里根据参数$E$判定。
猎物未成功逃脱，软进攻方式：
$$X(t+1)=(X_{rabbit}(t)-X(t))-E|J{X}_{rabbit}(t)-X(t)|,0.5\le |E|<1,r\ge 0.5$$
猎物未成功逃脱，硬进攻方式：
$$X(t+1)=X_{rabbit}(t)-E|\Delta X(t)|,|E|<0.5,r\ge 0.5$$
猎物成功逃脱，软进攻方式：
$$\begin{gathered} X(t+1)=\{\begin{array}{l}Y,f(Y)<f(X(t))\\ Z,f(Z)<f(X(t))\end{array} \\ Y=X_{rabbit}\left(t\right)-E|J{X}_{rabbit}\left(t\right)-X(t)| \\ Z=Y+S\ast LF(D),0.5\le |E|<1,r>0.5 \end{gathered}$$
猎物成功逃脱，软进攻方式：
$$\begin{gathered} X(t+1)=\{\begin{array}{l}Y,f(Y)<f(X(t))\\ Z,f(Z)<f(X(t))\end{array} \\ Y=X_{rabbit}\left(t\right)-E|J{X}_{rabbit}\left(t\right)-X_m(t)| \\ Z=Y+S\ast LF(D),|E|<0.5,r>0.5 \end{gathered}$$
其中，$LF$表示莱维飞行。
伪代码：

3.代码实现

% 哈里斯鹰算法
function [Best_pos, Best_fitness, Iter_curve, History_pos, History_best] = HHO(pop, maxIter,lb,ub,dim,fobj)
%input
%pop 种群数量
%dim 问题维数
%ub 变量上边界
%lb 变量下边界
%fobj 适应度函数
%maxIter 最大迭代次数
%output
%Best_pos 最优位置
%Best_fitness 最优适应度值
%Iter_curve 每代最优适应度值
%History_pos 每代种群位置
%History_best 每代最优位置
%% 初始化种群
X = zeros(pop, dim);
for i = 1:dim
    X(:,i) = rand(pop,1) * (ub(i) - lb(i)) + lb(i);
end
%% 记录
Best_pos=zeros(1,dim);
Best_fitness=inf;
Iter_curve=zeros(1,maxIter);
%% 迭代
t=0; 
while t<maxIter
    for i=1:size(X,1)
        % 边界检查
        FU=X(i,:)>ub;FL=X(i,:)<lb;X(i,:)=(X(i,:).*(~(FU+FL)))+ub.*FU+lb.*FL;
        fitness=fobj(X(i,:));
        if fitness<Best_fitness
            Best_fitness=fitness;
            Best_pos=X(i,:);
        end
    end
    
    E1=2*(1-(t/maxIter)); 
    for i=1:size(X,1)
        E0=2*rand()-1; %-1<E0<1
        Escaping_Energy=E1*(E0);  
        
        if abs(Escaping_Energy)>=1
            q=rand();
            rand_Hawk_index = floor(pop*rand()+1);
            X_rand = X(rand_Hawk_index, :);
            if q<0.5
                X(i,:)=X_rand-rand()*abs(X_rand-2*rand()*X(i,:));
            elseif q>=0.5
                X(i,:)=(Best_pos(1,:)-mean(X))-rand()*((ub-lb)*rand+lb);
            end
            
        elseif abs(Escaping_Energy)<1
            r=rand();
            
            if r>=0.5 && abs(Escaping_Energy)<0.5 
                X(i,:)=(Best_pos)-Escaping_Energy*abs(Best_pos-X(i,:));
            end
            
            if r>=0.5 && abs(Escaping_Energy)>=0.5  
                Jump_strength=2*(1-rand()); 
                X(i,:)=(Best_pos-X(i,:))-Escaping_Energy*abs(Jump_strength*Best_pos-X(i,:));
            end
            
            if r<0.5 && abs(Escaping_Energy)>=0.5 
                
                Jump_strength=2*(1-rand());
                X1=Best_pos-Escaping_Energy*abs(Jump_strength*Best_pos-X(i,:));
                
                if fobj(X1)<fobj(X(i,:)) 
                    X(i,:)=X1;
                else
                    X2=Best_pos-Escaping_Energy*abs(Jump_strength*Best_pos-X(i,:))+rand(1,dim).*Levy(dim);
                    if (fobj(X2)<fobj(X(i,:))) 
                        X(i,:)=X2;
                    end
                end
            end
            
            if r<0.5 && abs(Escaping_Energy)<0.5 
                Jump_strength=2*(1-rand());
                X1=Best_pos-Escaping_Energy*abs(Jump_strength*Best_pos-mean(X));
                
                if fobj(X1)<fobj(X(i,:)) 
                    X(i,:)=X1;
                else 
                    X2=Best_pos-Escaping_Energy*abs(Jump_strength*Best_pos-mean(X))+rand(1,dim).*Levy(dim);
                    if (fobj(X2)<fobj(X(i,:))) 
                        X(i,:)=X2;
                    end
                end
            end
        end
    end
    t=t+1;
    Iter_curve(t)=Best_fitness;
    History_best{t} = Best_pos;
    History_pos{t} = X;
end

end

%% Levy飞行
function o=Levy(d)
    beta=1.5;
    sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
    u=randn(1,d)*sigma;v=randn(1,d);step=u./abs(v).^(1/beta);
    o=step;
end

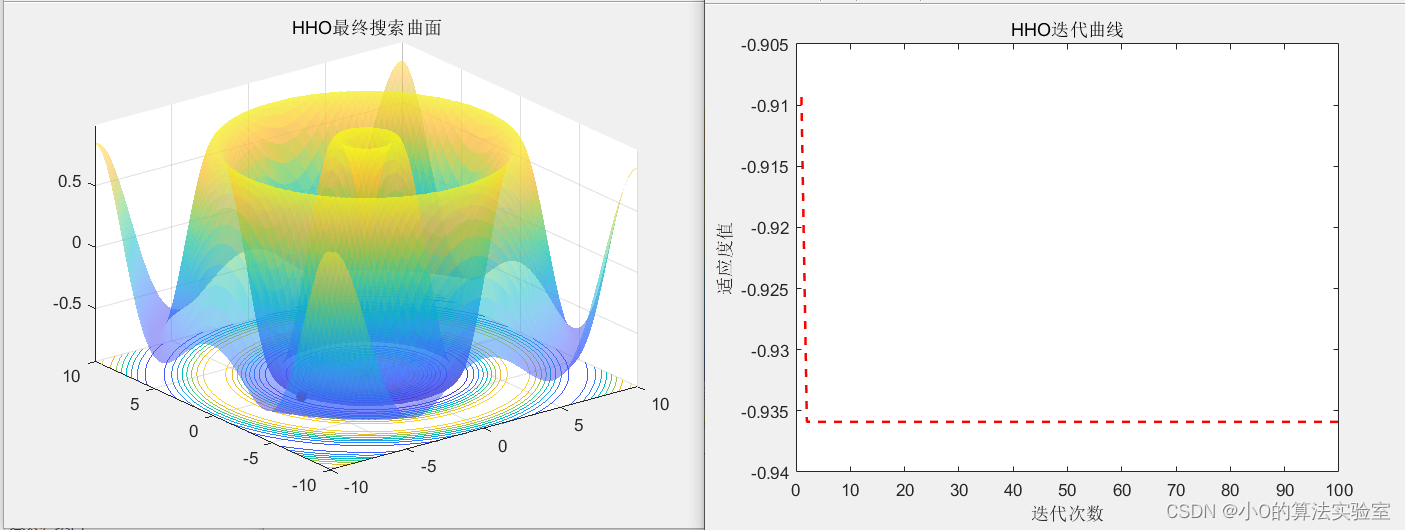
4.参考文献

[1] Heidari A A, Mirjalili S, Faris H, et al. Harris hawks optimization: Algorithm and applications[J]. Future generation computer systems, 2019, 97: 849-872.