数据结构与算法第五套大题

news2024/11/23 8:50:56

1.图的最小生成树，各边权值之和：

在这里插入图片描述
E={(1,5),(5,2),(5,3),(3,4)},W=10

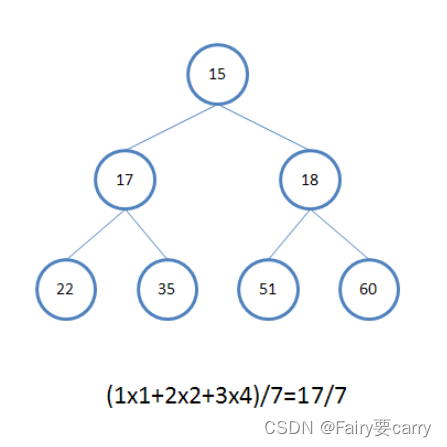
2.平均查找长度：

在这里插入图片描述
方法论： 直接将其变成一颗二叉树，然后计算每个节点的数学期望*比较次数之和/7
比如：
15为1/7，只需要比较一次（元素的比较次数直接看元素所在层数即可）
17为1/72
51为1/73
…
所以为17/7
在这里插入图片描述

3.线性探测法和链地址法解决哈希冲突：

在这里插入图片描述
1.线性探测法：

2.链地址法：

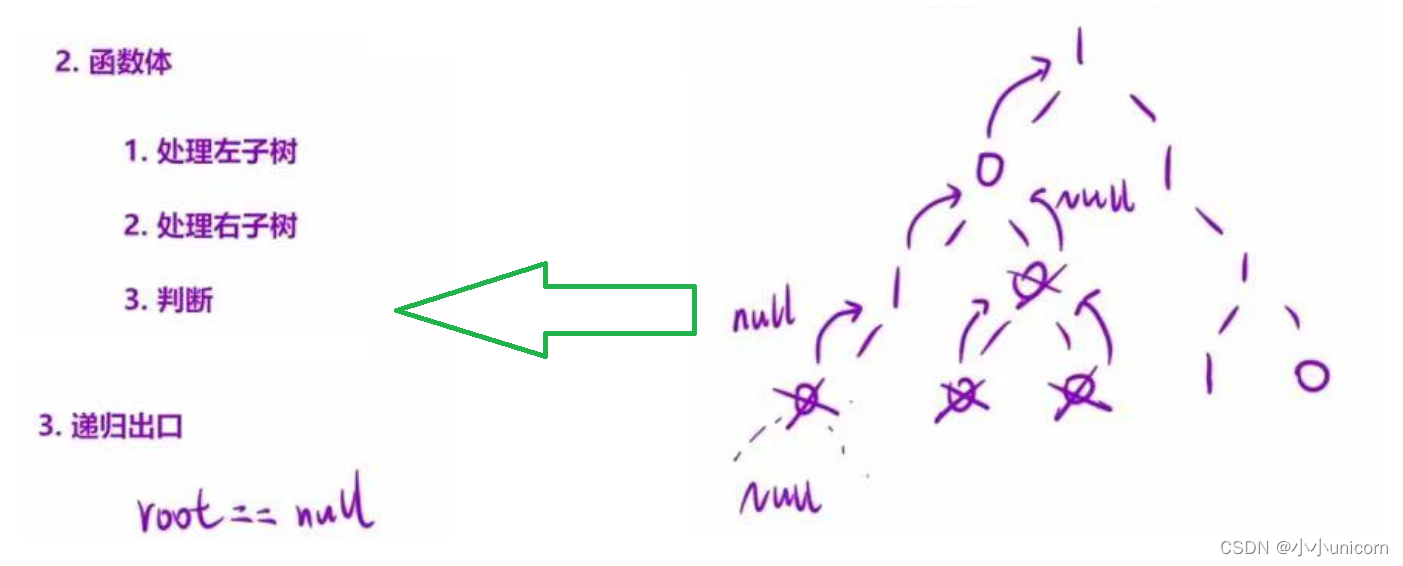
4.判断两个二叉树是否相同：

typedef struct node 
{
  datatype data; //数值
  struct node *lchild,*rchild; //左右子节点
} bitree;

bool judgebitree(bitree *bt1,bitree *bt2)
{
  if (bt1==NULL && bt2==NULL) 
      return true;
  else if(bt1==NULL||bt2==NULL||bt1->data!=bt2->data) 
      return false; //左右子树一方为空||左右子树节点值不一致
  else 
      return(judgebitree(bt1->lchild,bt2->lchild)&&judgebitree(bt1->rchild,bt2->rchild)); //递归两棵树的左右节点
}

5.两个有序单链表的合并排序算法

void mergelklist(lklist *ha,lklist *hb,lklist *&hc)
{
   lklist *s=hc=0;
   while(ha!=0 && hb!=0)
     if(ha->datadata)
     {
         if(s==0) 
             hc=s=ha; 
         else 
         {
             s->next=ha; 
             s=ha;
         }
         ha=ha->next;
     }
     else 
     {
         if(s==0) 
             hc=s=hb; 
         else 
         {
             s->next=hb; 
             s=hb;
         }
         hb=hb->next;
     }
     if(ha==0) 
         s->next=hb; 
     else 
         s->next=ha;
}