【C语言刷题】——初识位操作符
- 位操作符介绍
- 题一、 不创建临时变量(第三个变量),实现两个数的交换
- (1)法一
- (2)法二
- 题二、 求一个数存储在内存中的二进制中“一”的个数
- (1)法一
- (2)法二
- (3)法三
- 题三、 单身狗1
- (1)法一
- (2)法二
- 题四、 单身狗二
- (1)法一
- (2)法二
- (3)法三
位操作符介绍
位操作符有:
<< //左移操作符
>> //右移操作符
& //按位与
| //按位或
^ //按位异或
~ //按位取反
注:他们的操作数必须是整数。
更多关于位操作符介绍请看这篇文章:【C语言】——详解操作符(上)
题一、 不创建临时变量(第三个变量),实现两个数的交换
(1)法一
参考代码:
#include<stdio.h>
int main()
{
int a = 0;
int b = 10;
a = a + b;
b = a - b;
a = a - b;
printf("交换后a = %d b = %d\n", a, b);
return 0;
}
代码讲解:
相信这段代码大家都能看懂,这里我就不多解释了。
但遗憾的是这个方法有一点问题:当 a 和 b 的值很大(但都不超过 i n t int int 的存储空间)时,他们相加会超过 int 的存储空间,导致丢失数据。
那有什么更好的办法吗?有的,请看法二。
(2)法二
参考代码:
#include<stdio.h>
int main()
{
int a = 0;
int b = 10;
a = a ^ b;
b = a ^ b;
a = a ^ b;
printf("交换后a = %d b = %d", a, b);
return 0;
}
代码讲解:
首先,我们需掌握几个知识点:
- 一个数与他自身异或为 0 0 0 ,即: a a a ^ a a a == 0 0 0
- 任何数与 0 0 0 异或结果都为其本身,即: a a a ^ 0 0 0 == 0 0 0
- 异或运算满足交换律,即: a a a ^ a a a ^ b b b == a a a ^ b b b ^ a a a
第八行代码:
b = a ^ b;,由于第七行代码:a = a ^ b;,此时a = a ^ b;,即b = a ^ b ^ b,得b = a ^ 0;得 b = a
同理,第九行代码:
a = a ^ b;,由于第七行代码:a = a ^ b;和第八行代码结果b = a,即:a = a ^ b ^ a,得 a = b。
我们可以这样来理解:我们把第七行代码
a = a ^ b;当成是一把钥匙,碰到 a 得 b,碰到 b 得 a。
题二、 求一个数存储在内存中的二进制中“一”的个数
(1)法一
参考代码:
#include <stdio.h>
int main()
{
int num = 0;
scanf("%d", &num);
int count = 0;//计数
while (num)
{
if (num % 2 == 1)
count++;
num = num / 2;
}
printf("二进制中1的个数 = %d\n", count);
return 0;
}
代码讲解:
其实,
该法的解题思路与在十进制中打印每一位是思路相同。在十进制中,要想获得每一位,我们的方法是:先余十,再除十,不断循环。这里,也是一样的只是因为是二进制改为先余二,再除而,不断循环,遇到结果为 1 ,则计数器加一。
但是这个方法有点问题:它只能处理正数的情况,如果是负数,他就没办法了。为什么?因为:if(num % 2 == 1),负数余二永远不可能为 1,但num = num / 2;语句正常执行,输入复数的结果永远是 0。
(2)法二
参考代码:
#include<stdio.h>
int main()
{
int n = 0;
scanf("%d", &n);
int count = 0;
for (int i = 0; i < 32; i++)
{
if (n & 1)
{
count++;
}
n = n >> 1;
}
printf("%d", count);
return 0;
}
代码讲解:
法二的思路是:
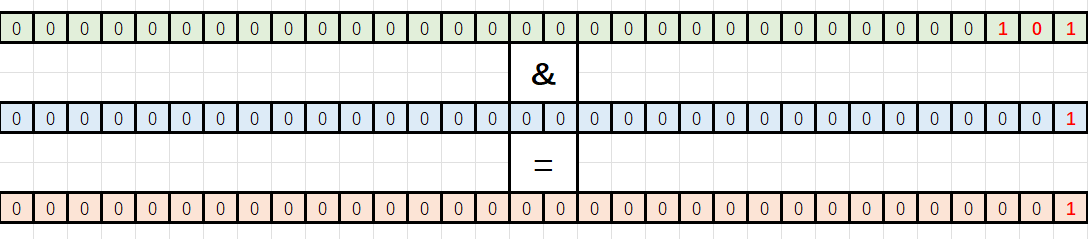
给这个数的每一位都与上 1 (不断右移),因为与的逻辑是:有 0 为 0,全 1 为 1。当运算结果为 0 ,表示该位为 0, 结果为 1 ,该位为 1
图解(以5为例):
结果为1,计数器加一
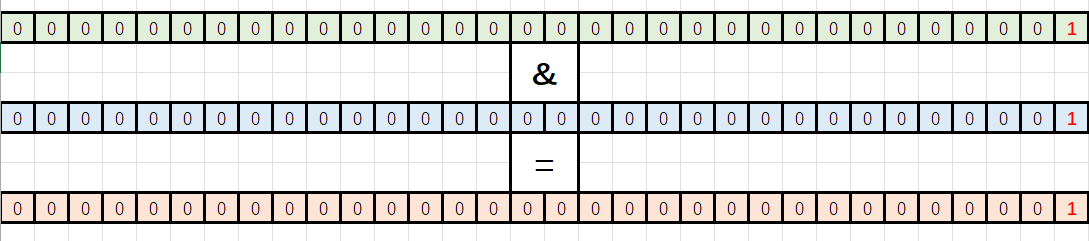
5右移一位:
结果为0,计数器不变
5再右移
结果为1,计数器加一
接着不断右移,一共32次,因为后面的结果都是0,变不再一一赘述。
但该方法一定要循环32次,有没有效率更高的方法呢?
(3)法三
参考代码:
#include<stdio.h>
int main()
{
int n = 0;
scanf("%d", &n);
int count = 0;
while (n)
{
n = n & (n - 1);
count++;
}
printf("%d", count);
return 0;
}
代码讲解:
该方法的核心:这个数本身与他自身减一做 与(&) 运算,不断循环
n = n & (n - 1);或许大家一脸疑惑,别急,直接上图!
以15为例:
循环一次
循环两次:
循环三次:
循环四次:
大家发现没有,
每循环一次就会把最右边的 1 给消去,当最终把所有 1 消去变成零,循环结束,而我们只需要计算循环了多少次就能知道该数有几个 1 。
题三、 单身狗1
题目:
在一个整型数组中,只有一个数字出现一次,其他数组都是成对出现的,请找出那个只出现一次的数字。
例如:数组中有:1 2 3 4 5 1 2 3 4,只有5出现一次,其他数字都出现2次,找出5
(1)法一
参考代码:
#include<stdio.h>
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 1, 2, 3, 4 };
int sz = sizeof(arr) / sizeof(arr[0]);
for (int i = 0; i < sz; i++)
{
int flag = 0;
int n = 0;
for (int j = 0; j < sz; j++)
{
if (i == j)
continue;
n = arr[i] ^ arr[j];
if (n == 0)
{
flag = 1;
break;
}
}
if (flag == 0)
printf("单身狗是:%d\n", arr[i]);
}
return 0;
}
代码讲解:
该方法想必大家都很容易想到,逻辑也很简单:遍历数组中的每一个数,每个数再遍历一遍除自身外的整个数组,遇到与自身一样的数就说明自己不是单身狗。
这里就不再过多解释
(2)法二
参考代码:
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 1, 2, 3, 4 };
int sz = sizeof(arr) / sizeof(arr[0]);
int a = 0;
for (int i = 0; i < sz ; i++)
{
a = arr[i] ^ a;
}
printf("单身狗是:%d\n", a);
return 0;
}
解题思路:
这里再带大家重温一下按位异或的相关知识:
(1)一个数与他自身异或为 0 0 0 ,即: a a a ^ a a a == 0 0 0
(2)任何数与 0 0 0 异或结果都为其本身,即: a a a ^ 0 0 0 == 0 0 0
那么综合运用起来就是这题的解法啦
将数组元素全部异或
a = 1 ^ 2 ^ 3 ^ 4 ^ 5 ^ 1 ^ 2 ^ 3 ^ 4
a = 1 ^ 1 ^ 2 ^ 2 ^ 3 ^ 3 ^ 4 ^ 4 ^ 5
a = 0 ^ 0 ^ 0 ^ 0 ^ 0 ^ 0 ^ 0 ^ 0 ^ 5
a = 5
题四、 单身狗二
题目:
一个数组中只有两个数字是出现一次,其他所有数字都出现了两次。
编写一个函数找出这两个只出现一次的数字。
例如:有数组的元素是:1,2,3,4,5,1,2,3,4,6
只有5和6只出现1次,要找出5和6.
(1)法一
参考代码:
#include<stdio.h>
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 1, 2, 3, 4,6 };
int sz = sizeof(arr) / sizeof(arr[0]);
int count = 0;
for (int i = 0; i < sz; i++)
{
int flag = 0;
int n = 0;
for (int j = 0; j < sz; j++)
{
if (i == j)
continue;
n = arr[i] ^ arr[j];
if (n == 0)
{
flag = 1;
}
}
if (0 == flag)
{
printf("单身狗是:%d\n", arr[i]);
count++;
}
if (2 == count)
break;
}
return 0;
}
代码讲解:
这段代码的思路与上一题单身狗一的法一思路是相同的,
即依次取出数组中的每个元素,让他与数组中剩下的元素比较,当遍历完整个数组依然没找到相同的数时,说明他是其中一个单身狗,计数器 +1 ,并打印;当计数器为二时,说明已找到全部单身狗,退出循环。
(2)法二
参考代码:
#include<stdio.h>
int main()
{
int arr[] = { 1,2,3,4,5,1,2,3,4,6 };
int sz = sizeof(arr) / sizeof(arr[0]);
int i = 0;
for (i = 0; i < 32; i++)
{
int j = 0;
int last_0 = 0;
int last_1 = 0;
for (j = 0; j < sz; j++)
{
if ((arr[j] & (1 << i)) == 0)
{
last_0 ^= arr[j];
}
else if ((arr[j] & (1 << i)) != 1)
{
last_1 ^= arr[j];
}
}
if(last_0 != 0 && last_1 != 0)
{
printf("%d %d", last_0, last_1);
break;
}
}
return 0;
}
代码讲解:
做了上面的单身狗,我们想这题应该也可以用异或分方法来解,
我们想到,如果将所有元素直接异或,肯定是无法直接找出两只单身狗,这时我们可以想到先将他们分组,让每一组都只有一只单身狗,再将两组全部异或就行了。那么怎么分组呢?
我们看到因为数组两两元素相同,加上两只单身狗,所以数组总数一定是偶数,这时我们可以依次遍历数组中所有元素的二进制位数,将该位为 1 和为 0 的元素分成两组,分完组后,若两组的元素个数都为奇数(相同的数该位一定相同,一定被分到同一组,剩下一只单身狗,为奇数),则成功将两只单身狗分开,再分别异或两组中的所有元素就能找出两周单身狗啦,
如果分完组两边都是偶数,则比较二进制下一位,直到分出奇数组。
(3)法三
参考代码:
#include<stdio.h>
void findTwoNum(int arr[], int n, int * pnum1, int * pnum2)
{
int i;
int sum = 0;
for (i = 0; i < 9; i++)
{
sum ^= arr[i];
} //先找到两个数互相异或的结果
int pos;
for (i = 0; i < 32; i++)
{
if (sum & 1 << i)
{
pos = i;
break;
}
} //再找到有分歧的一位。在这一位上,两个数一定是一个1一个0
*pnum1 = *pnum2 = 0;
for (i = 0; i < 10; i++)
{
if (arr[i] & 1 << pos)
{
*pnum1 ^= arr[i]; //这一位是1的,放在数1里
}
else
{
*pnum2 ^= arr[i]; //这一位是0的,放在数2里
}
}
}
代码讲解:
法二虽然用到了异或操作,但分起组来太过麻烦,
效率并不高,有没有什么方法能实现快速分组呢?答案当然是有的。
我们知道:两个相同的数异或为 0,将数组中的所有元素异或起来,得到的结果就是两只单身狗异或的结果。
这时我们可能就要问了,那得到这个结果有什么用呢?肯定不止唯二这两个数异或才得出这个结果,其他两个数异或也有可能得到这个结果。
确实如此,但我们别忘了异或的特点:
相同为 0,相异为 1。我们只需要找到异或的结果的其中一个为“ 1 ”的位数,这说明在这个位,其中一只单身狗是0,另一只为1。
这时,我们只需要将数组中的元素分两组:一组的元素在该位的值为 0,另一组该位值为 1,再将两组的所有元素分别异或起来,自然就得到两只单身狗啦。怎么样,是不是很巧妙呢。