1. 冯氏光照模型概述

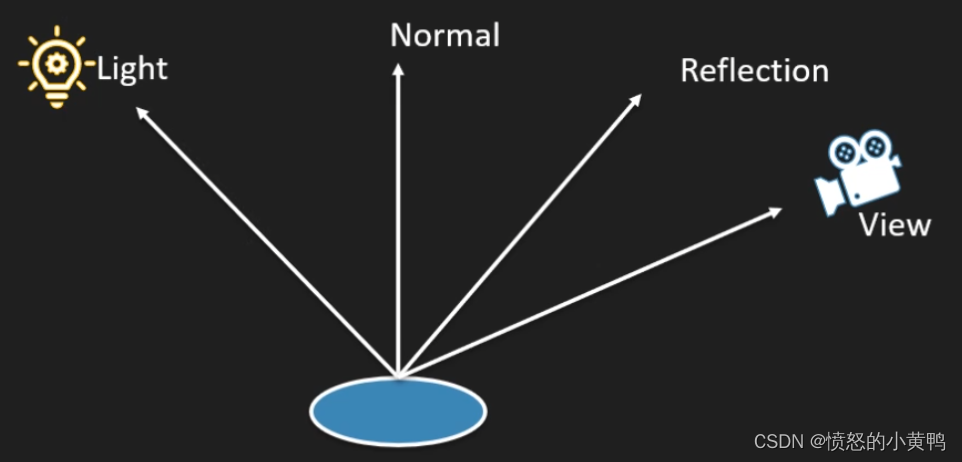
真实世界中的光照是及其复杂的，而且会受到诸多因素的影响，这是计算机在有限算力下无法模拟的。因此在计算机世界中会使用简化的模型来对现实模型进行模拟。这些模型都是基于对光的物理特性的理解。其中一个模型被称为冯氏光照(Phong Lighting Model)，冯氏光照模型主要由如下三个分量组成：

1. 环境光照(Ambient Lighting)
   即使在黑暗的情况下，世界上通常仍然有一些光亮(月亮、远处的光)，所以物体几乎永远不会是完全黑暗的。为了模拟这个，会使用一个环境光照常量，它永远给物体一些颜色

2. 漫反射光照(Diffuse Lighting)
   模拟光源对物体的方向性影响(Directional Impact)。它是冯氏光照模型中视觉上最显著的分量。物体的某一部分越是正对着光源，它就会越亮

3. 镜面光照(Specular Lighting)
   模拟有光泽物体上面出现的亮点。镜面光照的颜色相比于物体的颜色会更倾向于光的颜色

效果如下所示：

1.1 环境光照

光的一个属性是，它可以向很多方向发散并反弹，从而能够达到不是非常直接临近的点。所以光能够在其它的表面上反射，对一个物体产生间接的影响。考虑到这种情况的算法叫全局照明(Global Illuminate)算法，但这种算法即开销高昂又及其复杂。所以使用一个简化的全局照明模型，即环境光照

1.2 漫反射光照

漫反射示意图如下：

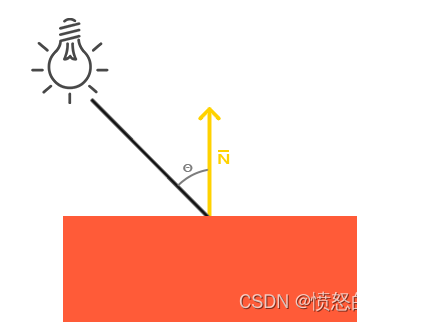
如果光线垂直于物体表面，这束光对物体的影响会最大化(更亮)。为了测量光线和片段的角度，使用一个叫法向量(Normal Vector)的东西，它是垂直与片段表面的一个向量。
由于两个单位向量的夹角越小，它们点乘的结果越倾向于1。当两个向量的夹角为90度的时候，点乘会变为0。这同样适用于θ，θ越大，光对片段颜色的影响就应该越小。为了得到两个向量夹角的余弦值，应该使用单位向量，所以需要确保所有的向量都是标准化得的，否则点乘的结果就不仅仅是余弦值了，理由如下：

点乘的公式：
$$\overrightarrow{OA}\cdot \overrightarrow{OB}=||\overrightarrow{OA}||\cdot ||\overrightarrow{OB}||cos(\theta )$$
当两向量的为单位向量时才有如下结果：
$$\overrightarrow{OA}\cdot \overrightarrow{OB}=1\cdot 1cos(\theta )$$

由此可以看出漫反射关照的计算需要以下内容：

1. 发向量
   一个垂直于顶点表面的向量
2. 定向的光线
   作为光源的位置与片段的位置之间向量查的方向向量。为了计算这个光线，我们需要光的位置向量和片段的位置向量

1.2.1 法向量

由于片段着色器里的计算都是在世界坐标系中的，所以应该把法向量(一般在局部坐标系)也转换为世界坐标系空间，但这不是简单的把它乘以一个模型矩阵就能搞定的。

首选，法向量只是一个方向向量，不能表示空间中的具体位置。同时，法向量没有齐次坐标(顶点中的w分量)，这意味着，唯一不应该影响法向量。因此，如果打算把法向量乘以一个模型矩阵，就要从模型矩阵中移除位移部分，比如使用3x3的矩阵，或者将4x4矩阵中的w分量设置为0。

其次如果模型矩阵执行了不等比的缩放，顶点的改变会导致法向量不再垂直于表面。效果如下：

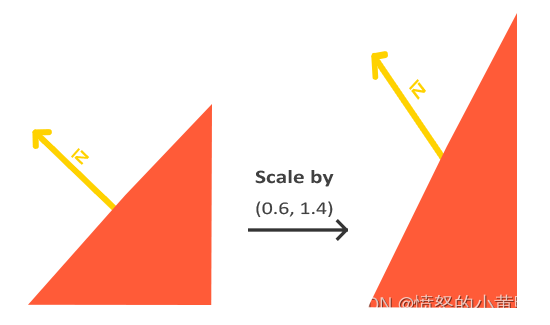
修复这个行为的诀窍是使用一个为法向量专门定制的模型矩阵，这个矩阵称之为法线矩阵(Normal Matrix)，它使用了一些线性代数的操作来移除对法向量不等比缩放的影响。在顶点着色器中，可以使用inverse和transpose函数生成这个法线矩阵，还要把被处理过的矩阵强制转换为3x3矩阵，赖堡镇它失去了位移属性以及能够乘以vec3的法向量，如下所示：

Normal = mat3(transpose(inverse(model))) * aNormal;

矩阵求逆是一项对于着色器开销很大的运算，因为它必须在场景中的每一个顶点上进行，所以应该尽可能地避免在着色器中进行求逆运算。

法线矩阵(Normal Matrix)的计算推到如下：
其中T为三角面的切线向量，N为法线向量，$N\cdot T=N^T\cdot T=0$。

1. 假设切线向量变换矩阵为M，变换后的切线向量 T' = M · T
2. 同时假设有一个正确的法线变换矩阵G，使得变换的法线 N' = G · N，那么变换后的N'点乘T'依然结果依然为0，由此可得出
   $$\begin{gathered} N^{\prime }\cdot T^{\prime }={N^{\prime }}^T{T}^{\prime }={(G\cdot N)}^{T}M\cdot T=N^T{G}^{T}MT \\ {N}^T\cdot T=N^T{G}^{T}MT \\ {G}^T\cdot M=I \\ G=(M^{-1}{)}^T \end{gathered}$$

原文-[图形学] 法向量变换矩阵的推导

1.3 镜面光照

和漫反射一样，镜面光照也决定与光的方向向量和物体的法向量，但也决定于观察方向。例如玩家是从什么方向看这个片段的

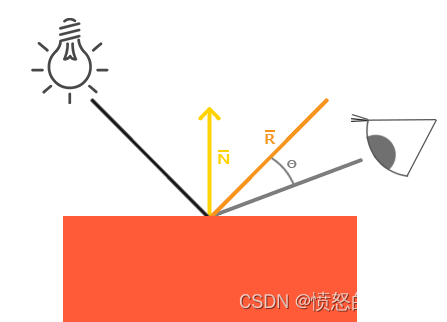
通过根据法向量翻折入射光的方向来计算反射向量。计算反射向量与观察方向的角度差，它们之间的角度越小，镜面光的作用越大。产生的效果是，看向在入射光在表面的反射方向时，会看到一个点高光。

观察向量是计算镜面光时需要的一个额外变量，可以使用观察者的世界空间位置和片段的位置来计算。大多数人趋向于在观察空间进行光照计算。在观察空间计算的优势是，观察者的位置总是在(0,0,0)

观察向量是从相机位置指向片段位置的向量

在光照着色器的早期，开发者曾经在顶点着色器中实现冯氏光照模型。在顶点着色器中做光照的优势是，相比片段来说，顶点要少得多，因此会更高效，所以（开销大的）光照计算频率会更低。然而，顶点着色器中的最终颜色值是仅仅只是那个顶点的颜色值，片段的颜色值是由插值光照颜色所得来的。结果就是这种光照看起来不会非常真实，除非使用了大量顶点。

在顶点着色器中实现的冯氏光照模型叫做高洛德着色(Gouraud Shading)，而不是冯氏着色(Phong Shading)。记住，由于插值，这种光照看起来有点逊色。冯氏着色能产生更平滑的光照效果。

1.4 冯氏光照公式

$I_{phong}=k_a{I}_{ambient}+{\sum }_{i=1}^{numLights}{I}_i(k_d(\overrightarrow{L_i}\cdot \vec{N})+k_s(\overrightarrow{R_i}\cdot \vec{V}{)}^{n^{shiny}})$

• $k_a{I}_{ambient}$ 表示环境光照，$k_a$代表环境光的系数
• ${\sum }_{i=1}^{numLights}$则表示多光源的处理
• $I_i$表示不同的光源
• $k_d(\overrightarrow{L_i}\cdot \vec{N})$表示漫反射光照，$k_d$表示漫反射光照系数
• $k_s(\overrightarrow{R_i}\cdot \vec{V}{)}^{n^{shiny}}$表示镜面光照，$k_s$表示镜面光照系数，$n^{shiny}$表示反光度(Shininess)，一个物体的反光度越高，反射光的能力越强，散射得越少，高光点就会越小，如下图所示：
  

1.5 着色器demo

1. 冯氏着色模式下的冯氏光照模型Demo
2. 高洛德着色模式下的冯氏光照模型Demo
3. 观察空间下计算的冯氏光照模型Demo

注：

• 前两个demo是在世界坐标系下进行的计算，最后一个则在观察空间下计算，在此空间下的观察者位置总是(0,0,0)

2. 材质

材质(Material)是用来描述物体颜色的属性，一个物体的材质通常包含环境光照(Ambient Lighting)、漫反射光照(Diffuse Lighting)、镜面光照(Specular Lighting)及是反光度(Shininess)组成。与上面的着色器demo的区别在于将物体颜色objectColor拆分为有多个分量组成的光。

struct Material {
    vec3 ambient;
    vec3 diffuse;
    vec3 specular;
    float shininess;
};

同时光本身也会存在属性的差别，如环境光、漫反射和镜面光应该有不同的强度表现。此时也需要将光本身(lightColor)拆分为不同的分量。

• 环境光通常会被设置为较弱的强度，这是因为不希望环境光颜色太过主导
• 漫反射分量通常被设置为希望光所具有的那个颜色，通常是一个比较明亮的白色
• 镜面光分量通常会保持为1.0，以最大强度的发光

struct Light {
    vec3 position;

    vec3 ambient;
    vec3 diffuse;
    vec3 specular;
};

2.1 demo

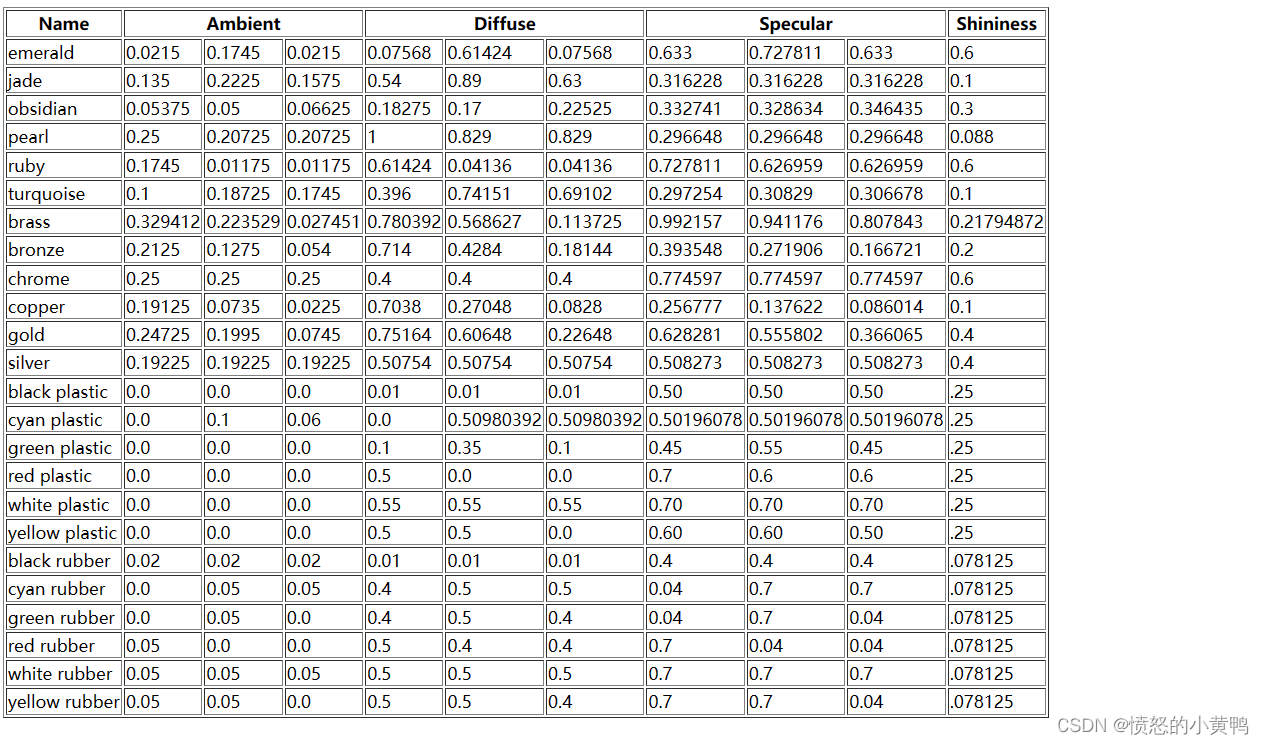
Learn OpenGL 上面也给出了一些材质的参数，大家可以根据material demo自行调整展示效果。这里放一个截图
原链接点这里

3. 光照贴图

在2. 材质一节中将整个物体的材质定义为了一个整体，但现实世界中的物体通常并不只包含一种材质。如一辆汽车，外壳会很亮，车床会部分反射周围的环境等等。所以那个材质的定义是不够的，现在需要对进行扩展，因此引入漫反射和镜面光贴图，这就允许对物体的漫反射分量(以及间接的对环境光分量，这两个几乎总是一样的)和镜面光分量有着更精确的控制

贴图的本质与纹理一致，只是在光照场景中，通常被叫做漫反射贴图(Diffuse Map)或镜面光贴图(Specular Map)，它是一个表现了物体所有漫反射或镜面光颜色的纹理图像。最后在着色器中采样这些颜色做为漫反射或镜面光颜色即可。

还有一种是放射光贴图(Emission Map)，它是一个储存了每个片段的发光值(Emission Value)的贴图。发光值是一个包含（假设）光源的物体发光(Emit)时可能显现的颜色，这样的话物体就能够忽略光照条件进行发光(Glow)。游戏中某个物体在发光的时候，你通常看到的就是放射光贴图（比如 机器人的眼，或是箱子上的灯带）。因为放射光贴图本身包含了发光值，因此可以不用乘以光源等值，而直接作为结果进行输出显示

3.1 demo

光照贴图Demo

4. 投光物

将光投射(Cast)到物体的光源叫做投光物(Light Caster)。

4.1 平行光

当光源处于很远的地方时，来自光源的每条光线就会近似于互相平行。不论物体和(或)观察者的位置，看起来好像所有的光都来自于同一个方向。当我们使用一个假设光源处于无限远处的模型时，它就被称为定向光(Direction Light)(如太阳)，因为它的所有光线都有着相同的方向，它与光源的位置是没有关系的。

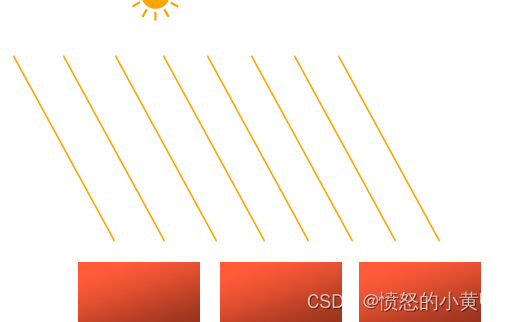
因为所有的光线都是平行的，所以物体与光源的相对位置是不重要的。因此可以定义个光线向量而不是位置向量来模拟一个定向光(将light.position修改为light.direction)。 定向光对于照亮整个场景的全局光源是非常有效的。

4.1.1 平行光Demo

平行光Demo

4.2 点光源

通常在一个场景中往往还会存在一些点光源(Point Light)。点光源是处于世界中某一个位置的光源，它会朝着所有方向发光，但光线会随着距离逐渐衰弱。 常见的如灯泡，火把等。

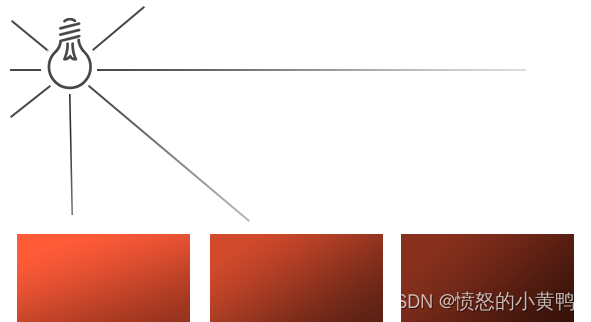
4.2.1 衰减

随着光线传播距离的增长逐渐削减光的强度的过程通常叫做衰减(Attenuation)。这种随距离减少光强度的方式是一种线性方程。然而最终的效果会比较假。现实中灯在近处会非常凉，但随着距离的增加光源的强度一开始会下降非常快，但在远处时剩余的光强度就会下降的非常慢。 公式如下：

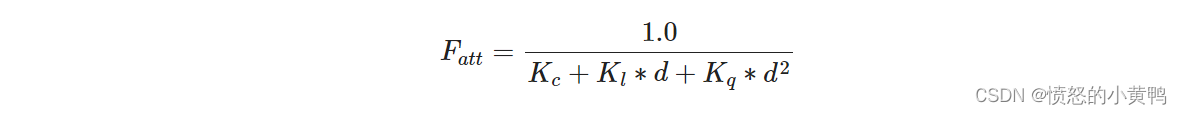
$d$表示片段距光源的距离，$K_c$为常数项，$K_l$为一次项，$K_q$为二次项

• 常数项通常保持为1.0，主要作用是保证分母永远不会比1小，否则的话在某些距离上它反而会增加亮度
• 一次项与距离值相乘，以线性的方式减少强度
• 二次项与距离的平方相乘，让光源以二次递减的方式减少强度。二次项在距离比较小的时候影响会比一次项小很多，但当距离只比较大的时候它就会比一次项影响更大了

最终的结果就是，光在近距离时亮度很高，但随着距离变远亮度迅速降低，随后会以更慢的速度减少。关于$K_c$、$K_l$、$K_q$的选值通常会受环境、希望光覆盖的距离、光的类型等因素影响，但在大多数时候这都是经验值。下表给出一些常见的设置：

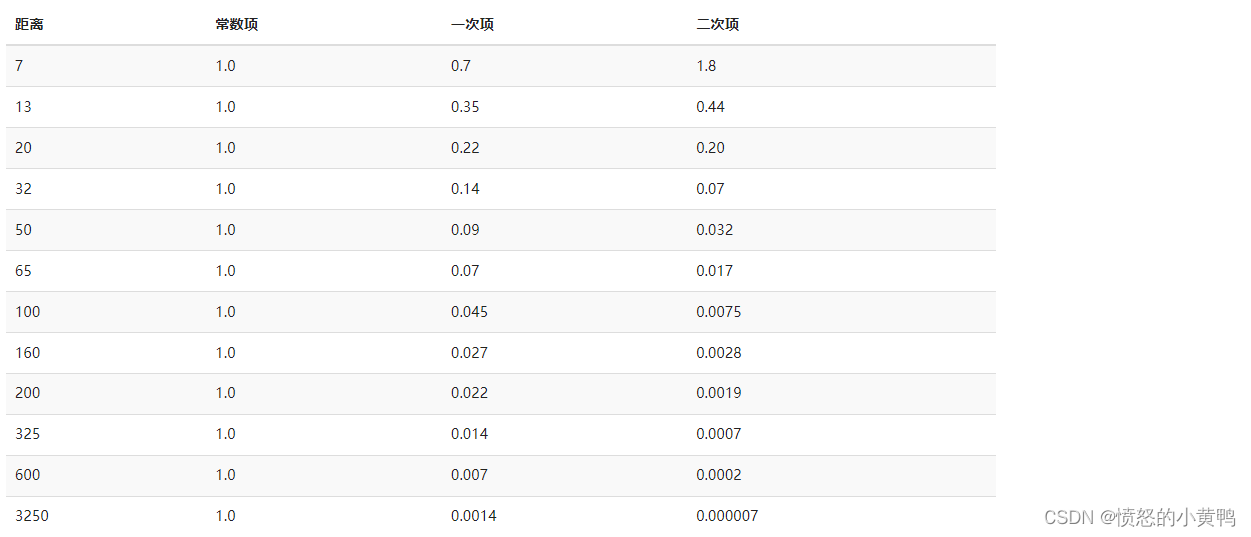
4.2.1 点光源Demo

点光源Demo

4.3 聚光

聚光(Spotlight)是位于环境中某个位置的光源，它只朝一个特定方向照射光线。这样就会造成只有在聚光方向的特定半径内的物体才会被照亮，其它的物体都会保持黑暗。

在OpenGL中聚光用一个世界空间位置、一个方向和一个切光角(Cutoff Angle)表示。 切光角指了聚光的半径(圆锥半径)。聚光的工作原理图如下：

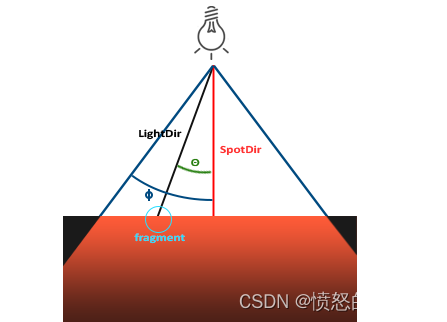
• LightDir: 从片段指向光源的向量
• SpotDir: 聚光所指的方向
• φ: 指定聚光半径的切光角。落在这个调度之外的物体不会被这个聚光所照亮
• θ: LightDir向量和SpotDir向量之间的夹角，在聚光内部的话θ值应该比φ值小

所以最终需要计算θ角，并与φ进行比较，大于φ的部分不会被这个聚光所照亮

4.3.1 聚光Demo

聚光Demo

4.3.2 平滑/软化边缘

为了创建一种看起来边缘平滑的聚光，需要聚光有一个内圆锥(Inner Cone)和一个外圆锥(Outer Cone)。

如果一个片段处于内外圆锥之间，将会给它计算出一个0到1的光照强度。如果片段在圆锥之内，它的强度就是1,。如果在外圆锥之外强度就是0。公式如下：

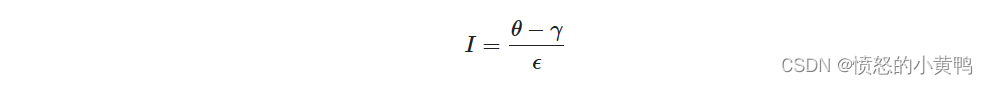
• ε(Epsilon): 内(θ)外(γ)圆锥之间的余弦值之差
• I: 当前片段聚光强度

4.3.2.1 聚光 平滑/软化边缘 Demo

聚光 平滑/软化边缘 Demo

5. 多光源合并

多光源的合并就是将几个种类的光源进行合并处理，具体的可以参考OpenGL 多光源

5.1 多光源合并Demo

多光源合并Demo