还在HACK,代码仅供参考。
A. Rudolf and the Ticket
关键句,直接枚举所有可能

#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define all(x) x.begin(),x.end()
#define fr first
#define se second
#define endl '\n'
using namespace std;
void solve(){
int n,m,k;
cin>>n>>m>>k;
int b[n+1];
per(i,1,n)cin>>b[i];
int c[m+1];
per(i,1,m)cin>>c[i];
//bf + cs <=k
int ans=0;
per(i,1,n){
per(j,1,m){
if(b[i]+c[j]<=k)ans++;
}
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
cin>>t;
while(t--)solve();
return 0;
}B - Rudolf and 121
你可以对序列进行的操作如下(可以进行0次或者无数次)

问你最后是否可以将序列全部变成0
这个操作考虑起来可能会有点麻烦,我们转变一下就是第一个数减1,第二个数减2,第三个数减1
然后循环判断就可以了,注意不能一个一个去减,因为要减到0(模拟的话就要TLE了),所以a[i]本身是要直接变成0的。也就是直接减a[i]的值。
#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define all(x) x.begin(),x.end()
#define fr first
#define se second
#define endl '\n'
using namespace std;
const int N=2e5+5;
int a[N],n;
void solve(){
cin>>n;
per(i,1,n)cin>>a[i];
//中间的减二 两边的减一
//a[i]--,a[i+1]-2,a[i+2]-1
per(i,1,n-2){
if(a[i]*2<=a[i+1] and a[i]<=a[i+2]){
a[i+1]-=a[i]*2;
a[i+2]-=a[i];
}else{
cout<<"NO"<<endl;
return;
}
}
if(a[n] or a[n-1]){//最后记得判断这两个是否减完了
cout<<"NO"<<endl;
}else cout<<"YES"<<endl;
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
cin>>t;
while(t--)solve();
return 0;
}C - Rudolf and the Ugly String
如果一个字符串里面有子串(连续的)“map”或者“pie”那就是一个丑陋的字符串。
可以减去任意位置上的一个字符,最少减几个字符可以让字符串变得漂亮。
因为是连续的,所以遇到“map“的时候考虑删哪一个,删m可能左边会连个m过来,删p右边可能会连个p过来,所以删中间那个是最优解(因为“maap“是漂亮的),“pie“也同理删 i。
但是这里要考虑一个特殊情况(提交WA了一次之后发现的):“mapie”,这里有两个丑陋的子串,但是只需要操作一次就可以带走他们两个,即删p。
往后枚举每一个位置,优先删除“mapie“
#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define all(x) x.begin(),x.end()
#define fr first
#define se second
#define endl '\n'
using namespace std;
void solve(){
string s;
cin>>s>>s;
//拥有pie或者map就是丑陋的
//删掉最少的让他变美丽
//map
int ans=0;
int now=0;
while(now<=s.length()-1){
if(now+4<=s.length()-1 and s[now]=='m' and s[now+1]=='a' and s[now+2]=='p' and s[now+3]=='i' and s[now+4]=='e'){
ans++;
now=now+5;
}else if(now+2<=s.length()-1 and s[now]=='m' and s[now+1]=='a' and s[now+2]=='p'){
ans++;
now=now+3;
}else if(now+2<=s.length()-1 and s[now]=='p' and s[now+1]=='i' and s[now+2]=='e'){
ans++;
now=now+3;
}else now++;
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
cin>>t;
while(t--)solve();
return 0;
}D. Rudolf and the Ball Game
惊天大模拟!

一共有6个人顺时针围成一个圈,一共有3次操作,球当前在第2个人手上。
2 ?的意思就是不知道顺时针还是逆时针,球传了2个距离。
如果问号是0,那么代表顺时针,问号是1代表是逆时针。
问这些操作之后,球有可能在哪些人手里。
比较良心的是传的距离给你定好了,要不然还得推式子![]()
模拟的时候记得用set,假如一直问号,球一分为二每次都传到同一个人手里,时间和空间就要爆开了,同一个人操作一次就行。
#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define all(x) x.begin(),x.end()
#define fr first
#define se second
#define endl '\n'
using namespace std;
void solve(){
int n,m,x;
cin>>n>>m>>x;
//球在x身上
int r[m+1];
char c[m+1];
per(i,1,m)cin>>r[i]>>c[i];
//每轮丢的距离是r
//方向是c
//当前球在玩家x身上,排名是顺时针升序
set<int>q;
q.insert(x);//球在谁身上
set<int>nxtq;//不需要队列 重复的不需要
per(i,1,m){
//每一轮都对队列进行操作,更新到nxtq里面
if(c[i]=='0'){//顺时针丢
for(auto now:q){
//1 2 3 4 5 6 7
now+=r[i];
if(now%n==0)now=n;
else now%=n;
nxtq.insert(now);
}
}else if(c[i]=='1'){//逆时针丢
for(auto now:q){
//1 2 3 4 5 6 7
now-=r[i];
//0对n, -1对n-1 -2对n-2
if(now<=0)now=n+now;
nxtq.insert(now);
}
}else{//两个方向都丢
for(auto now:q){
int tmp=now;
//now更新两次
now+=r[i];
if(now%n==0)now=n;
else now%=n;
nxtq.insert(now);
now=tmp;
now-=r[i];
//0对n, -1对n-1 -2对n-2
if(now<=0)now=n+now;
nxtq.insert(now);
}
}
//更新完了放回去
q.clear();
for(auto j:nxtq)
q.insert(j);
nxtq.clear();
}
cout<<q.size()<<endl;
for(auto i:q)cout<<i<<" ";
cout<<endl;
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
cin>>t;
while(t--)solve();
return 0;
}E. Rudolf and k Bridges
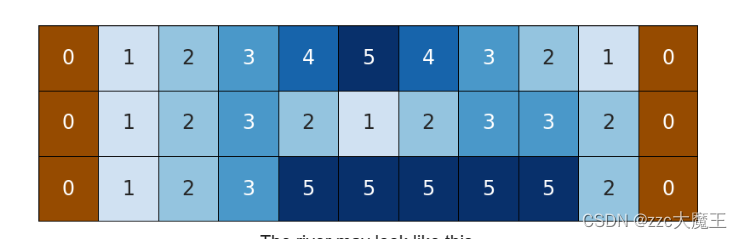
中间是河,左右两边必定是0,搭桥。
桥下面有支柱(最左边最右边必定要放一个),支柱的费用是当前单元格的值+1。
任意相邻两个支柱的距离x,y,有abs(x-y)-1<=d
也就是假如d=2,x<y,那么x=1时,y=4是极限,y=x+d+1。
那么当前 桥的支柱花费 就 比较明显的就能看出来是线性dp了。

假设我们对这一行搭桥,两个支柱的距离假定只有这些

也就是我们往后面的范围搭桥,1,2,3这里必须要放一个才能扩大当前能建的范围,也就是后面和前面有关。(如果 1 放了 3后面解锁了一个很大很大的数,而2后面在很大的数后面解锁了一个1,那显然要选2搭支柱,而不是第一个上面)
直接给出定义,dp[i]为在 i 处建造支柱最小的花费。
状态转移也很显然,在合法范围 dp[i-d-1]~dp[i-1] 里面找最小值
//下标 i-d-1 的位置有支柱,最远可以让下标 i 位置造一个支柱
即 dp[i]=min{dp[i-d-1]~dp[i-1]}+a[i][j]+1
题目还说了造一个桥没意思,要下标连着造k个桥,输出最小的花费。
那就最后对dp数组进行前缀和,连续k个都枚举一遍就行了。
per(i,1,n){
per(j,1,m){
cin>>a[i][j];
dp[i][j]=MAX;
}
dp[i][1]=1;
per(j,2,m){
//j-1 ,d=0
//j-2 ,d=1
//j-d-1
int r=1>(j-d-1)?1:(j-d-1);
rep(l,j-1,r)
dp[i][j]=min(dp[i][j],dp[i][l]+a[i][j]+1);
}
}但是这样求dp数组还不够,复杂度最差能达到N*M*D,N=100,M=2e5,D=2e5。
极限情况下是能卡掉的,N和M没法优化,想办法降低D的复杂度(即找最小值)。
因为一直都是找前面的最小值,看起来就有点类似滑动窗口这种东西,直接用单调队列维护dp数组做到让复杂度变成NM,就可以通过了。
题目还卡了一手内存和范围,最坏情况a全部造上支柱花费1e6*2e5 超过了21亿的int大小,但是define int long long大概率是要MLE的,所以只能对dp开long long,
#include <bits/stdc++.h>
//#define int long long
#define per(i,j,k) for(int (i)=(j);(i)<=(k);++(i))
#define rep(i,j,k) for(int (i)=(j);(i)>=(k);--(i))
#define debug(a) cout<<#a<<"="<<a<<endl
#define all(x) x.begin(),x.end()
#define fr first
#define se second
#define endl '\n'
using namespace std;
const int N=105,M=2e5+5;
const long long MAX=LONG_LONG_MAX>>2;
int a[N][M];
long long dp[N][M];
//1e6*2e5
//最差情况3e11大小
void solve(){
int n,m,k,d;
cin>>n>>m>>k>>d;
per(i,1,n){
per(j,1,m){
cin>>a[i][j];
dp[i][j]=MAX;
}
dp[i][1]=1;
deque<array<long long,2>>q;
//下标,值
q.push_back({1,1});
per(j,2,m){
//每一个单元格的价值
//最好是一次就访问出答案
int val=a[i][j]+1;//当前单元格的值
int r=1>(j-d-1)?1:(j-d-1);
while(q.size() and q.front()[0]<r)q.pop_front();//过期了
dp[i][j]=q.front()[1]+val;//维护的最小的+当前单元格值为当前dp值
while(q.size() and dp[i][j]<=q.back()[1])q.pop_back();
q.push_back({j,dp[i][j]});
//单调队列好像能维护
//{r,j-1}的范围拿出一个最小的dp[i][j]
//j-1 ,d=0
//j-2 ,d=1
//j-d-1
// rep(l,j-1,r)
// dp[i][j]=min(dp[i][j],dp[i][l]+a[i][j]+1);
//转移方程需要优化
//如果推进来的更小,前面就不需要了
}
}
// per(i,1,n)cout<<dp[i][m]<<endl;
// return;
//j1+d 即下一个支撑位置
//任选一行造一个桥
//cost=2+[支撑对里面的]
//支撑对距离小于等于d
//d=2
//1,4
//i+d+1范围里必须要造一个桥
//线性dp
//定义dp[i]为从第一个数
//选到目前的最小价值
//从前面合法范围转移一个最小值过来
//可能要开long long了
per(i,2,n){
dp[i][m]+=dp[i-1][m];
}
// per(i,2,n){//变成前缀和
// dp[i][m]+=dp[i-1][m];
// }
//处理连续k个桥的问题
long long ans=LONG_LONG_MAX;
per(i,k,n){
ans=min(ans,dp[i][m]-dp[i-k][m]);
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(false),cin.tie(nullptr);
int t=1;
cin>>t;
while(t--)solve();
return 0;
}