数据结构 图 3月11日 – 天气:晴
晚上无线网络突然不能用了,花费好久弄这个,耽误了一些时间
1. 图的定义

这里需要注意完全图的定义,以及完全图的边数

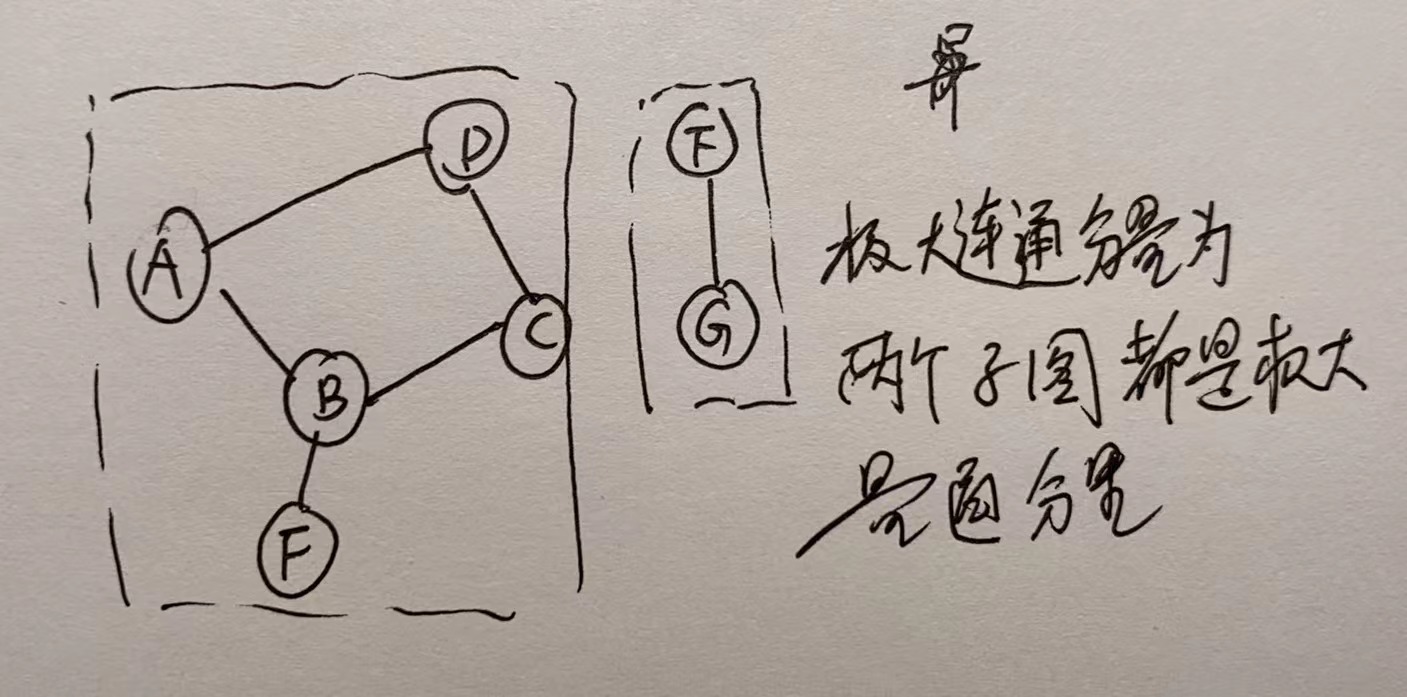
这里需要注意连通图和连通分量的概念。
2. 图的存储结构
图有两种存储结构,分别是邻接矩阵和邻接表。
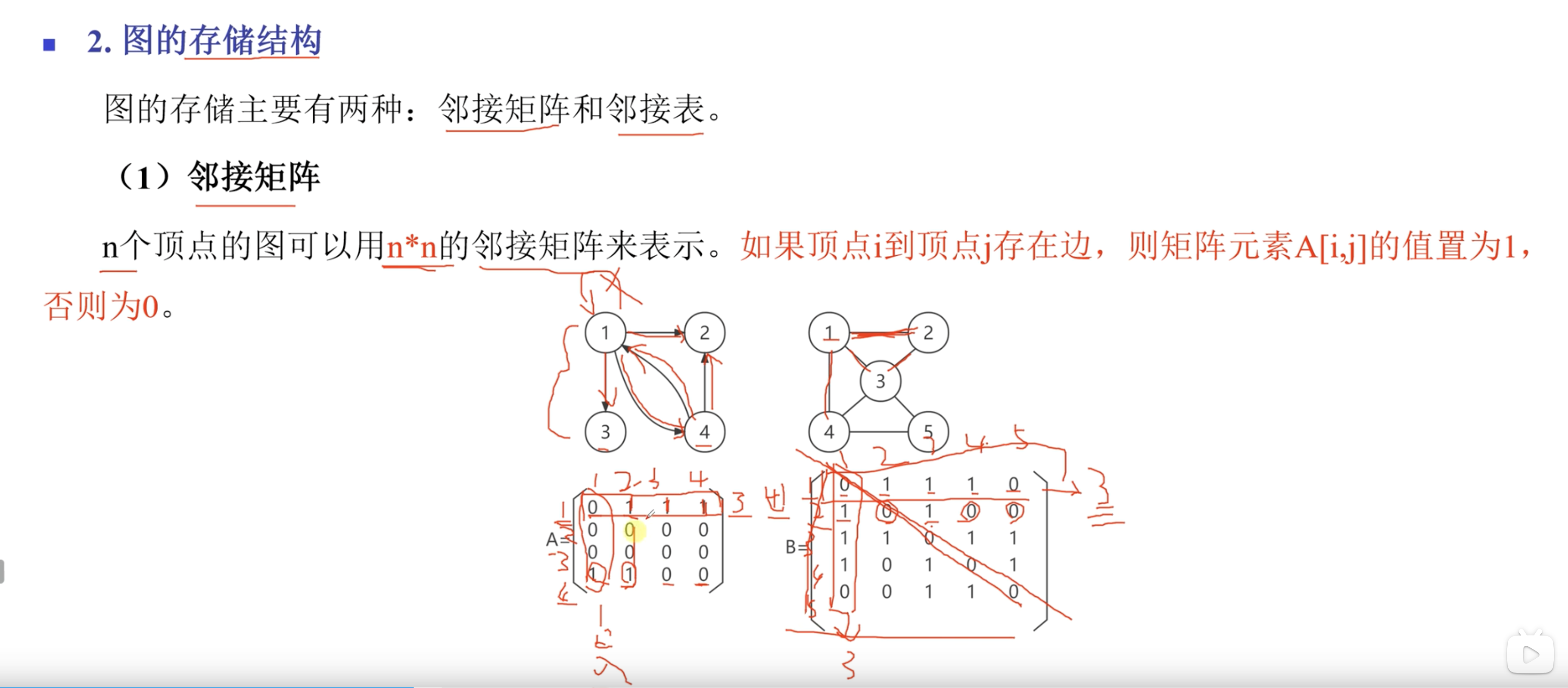
对于有向图来说,邻接矩阵中每一行1的个数代表了该节点的出度。每一列中1的个数代表了该节点的入度。
对于无向图来说,每一行或每一列1的个数代表了节点的度。
从图中可以看出来,邻接矩阵的存储方式只和节点的个数有关

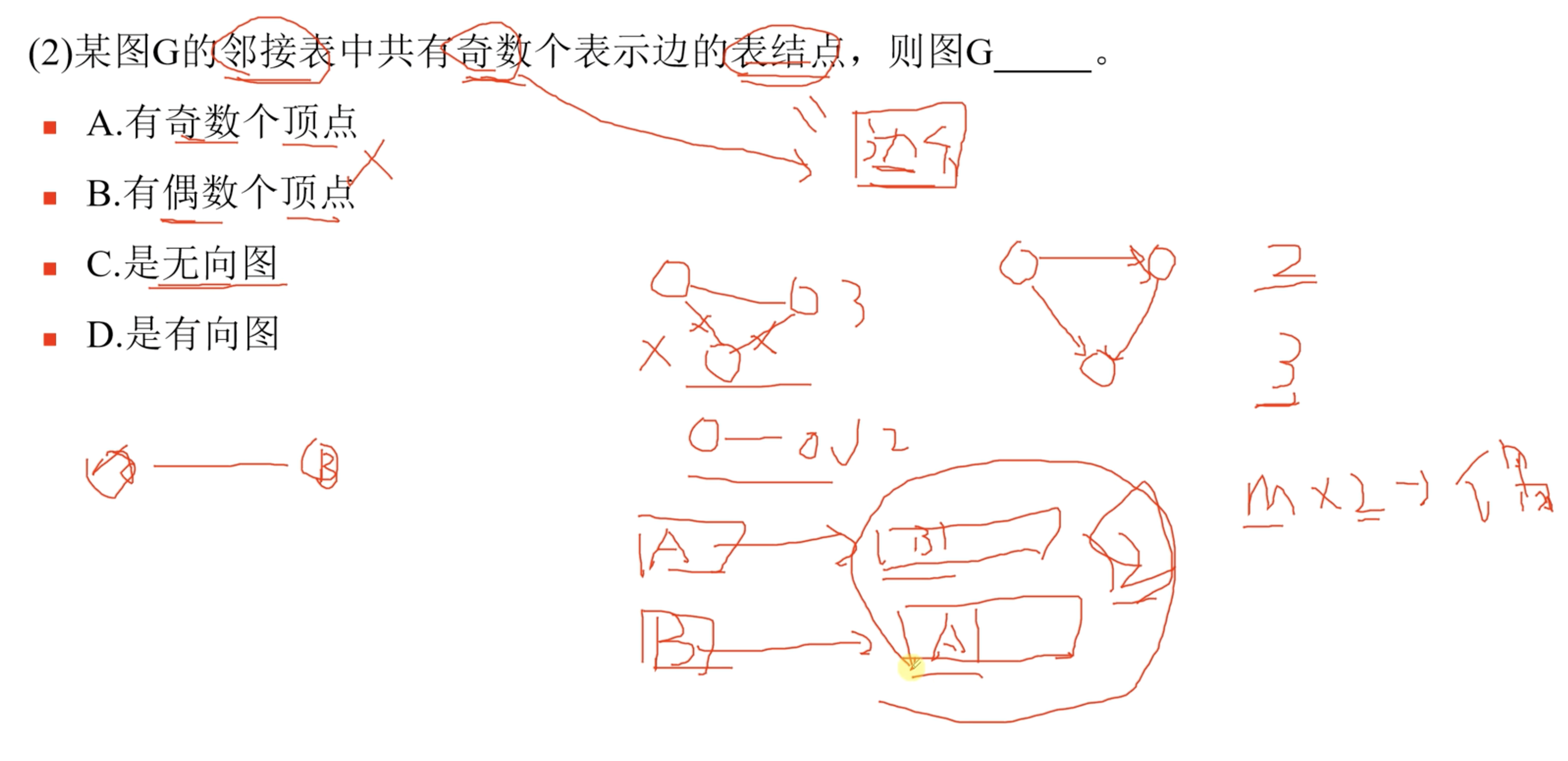
邻接表的存储方式的特点是,链表中的每一个节点代表图中的一条边。链表中节点的个数等于边的个数。
对于无向图来说,链表中的节点必然是偶数个。

3. 图的遍历方式
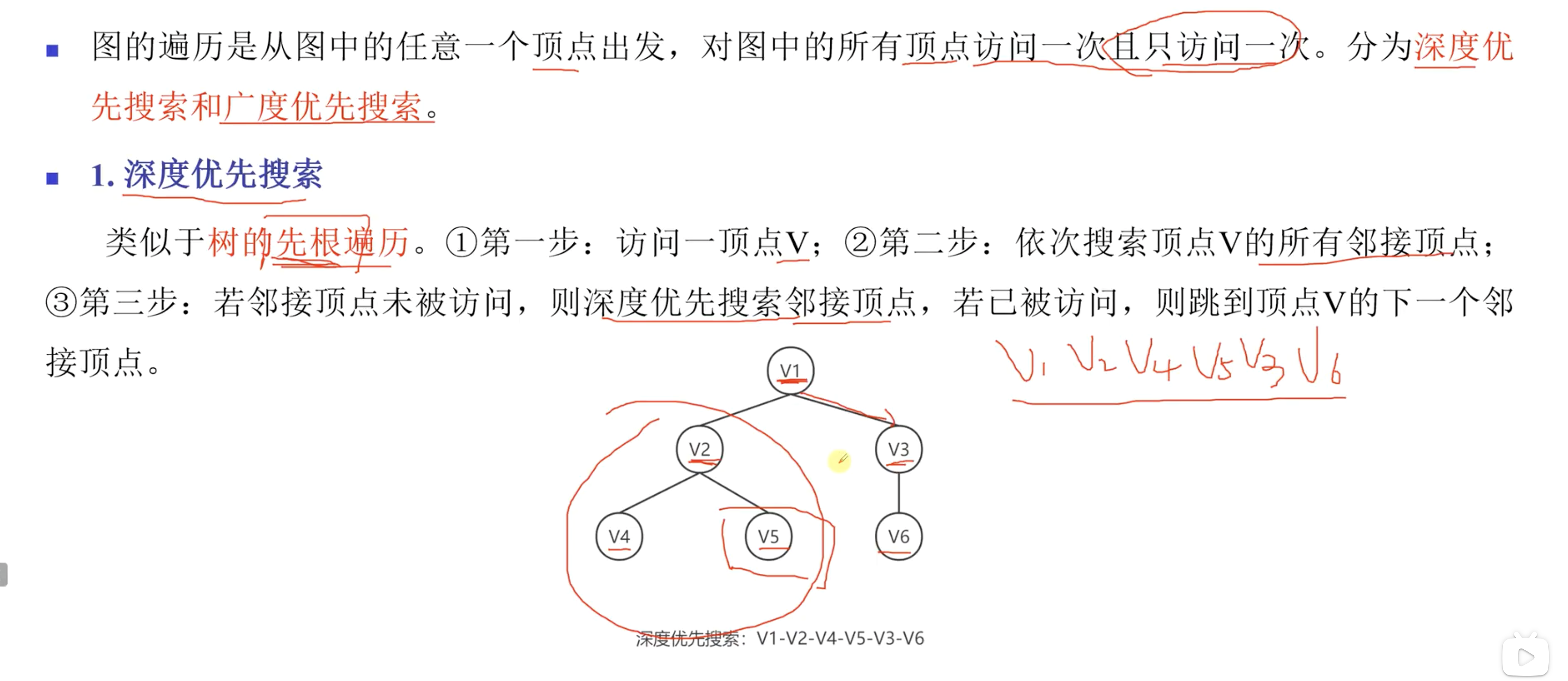
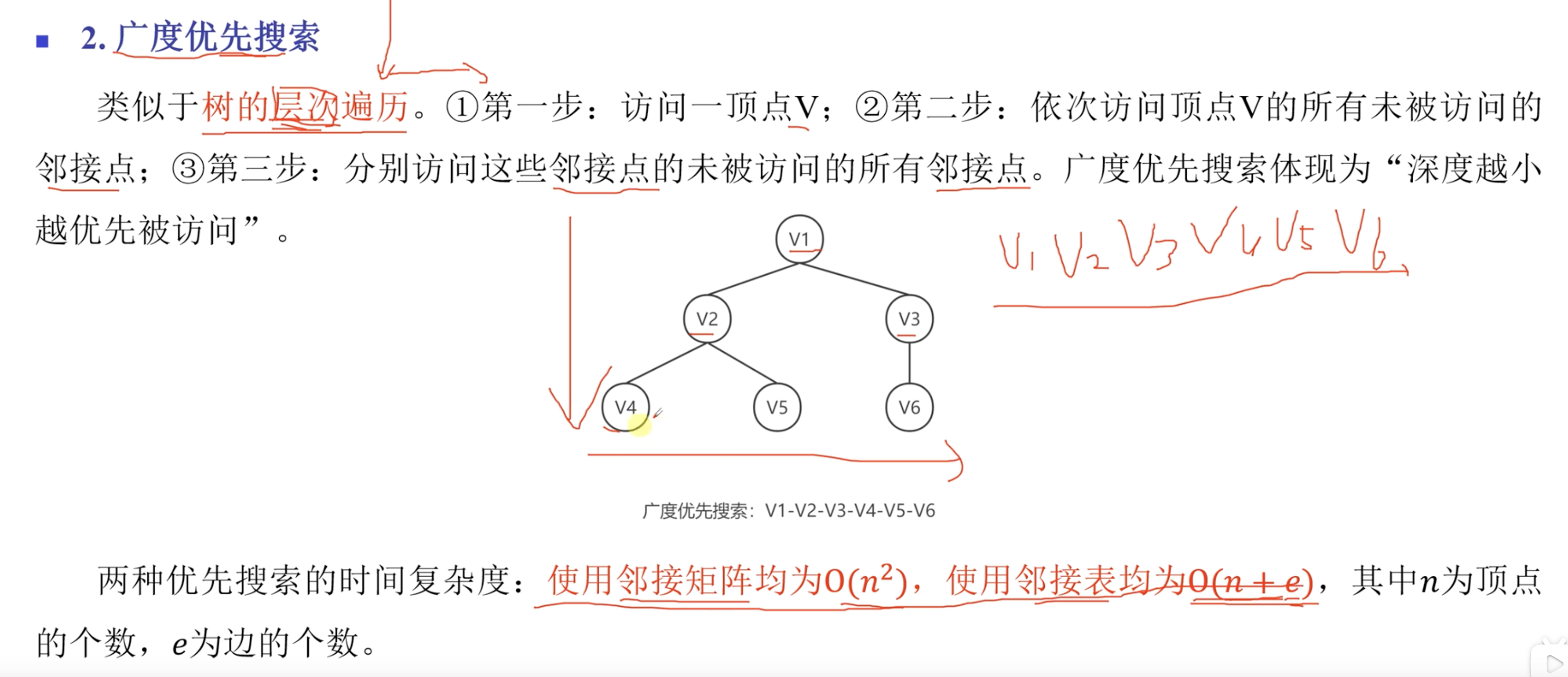
这里需要重点记住遍历不同存储方式的图的时间复杂度

4. 图的最小生成树

计算最小生成树的两种算法

Prim算法每次选择一条权值最小的边,并选择出顶点,然后从已经生成的部分中选择一条最小的边与已经生成的部分连接,直到所有的顶点都相连。时间负责度为n^2
它只和顶点的个数有关,因此适用于稠密图(顶点多,边少)
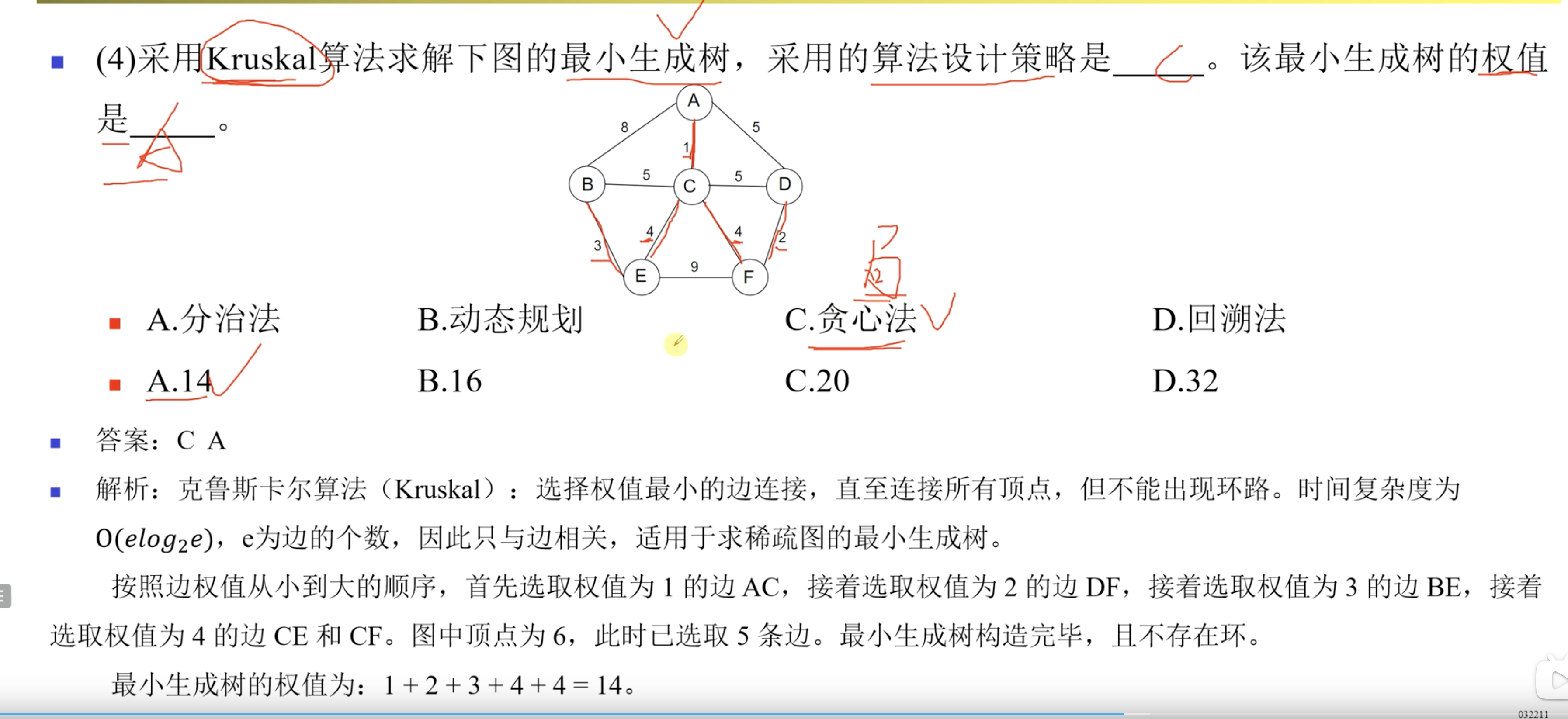
Kruskal算法每一次都选择图中最小的一条边,直到所有的顶点都被连接。
它只和边的个数有关,因此适用于稀疏图。
5. 拓扑排序
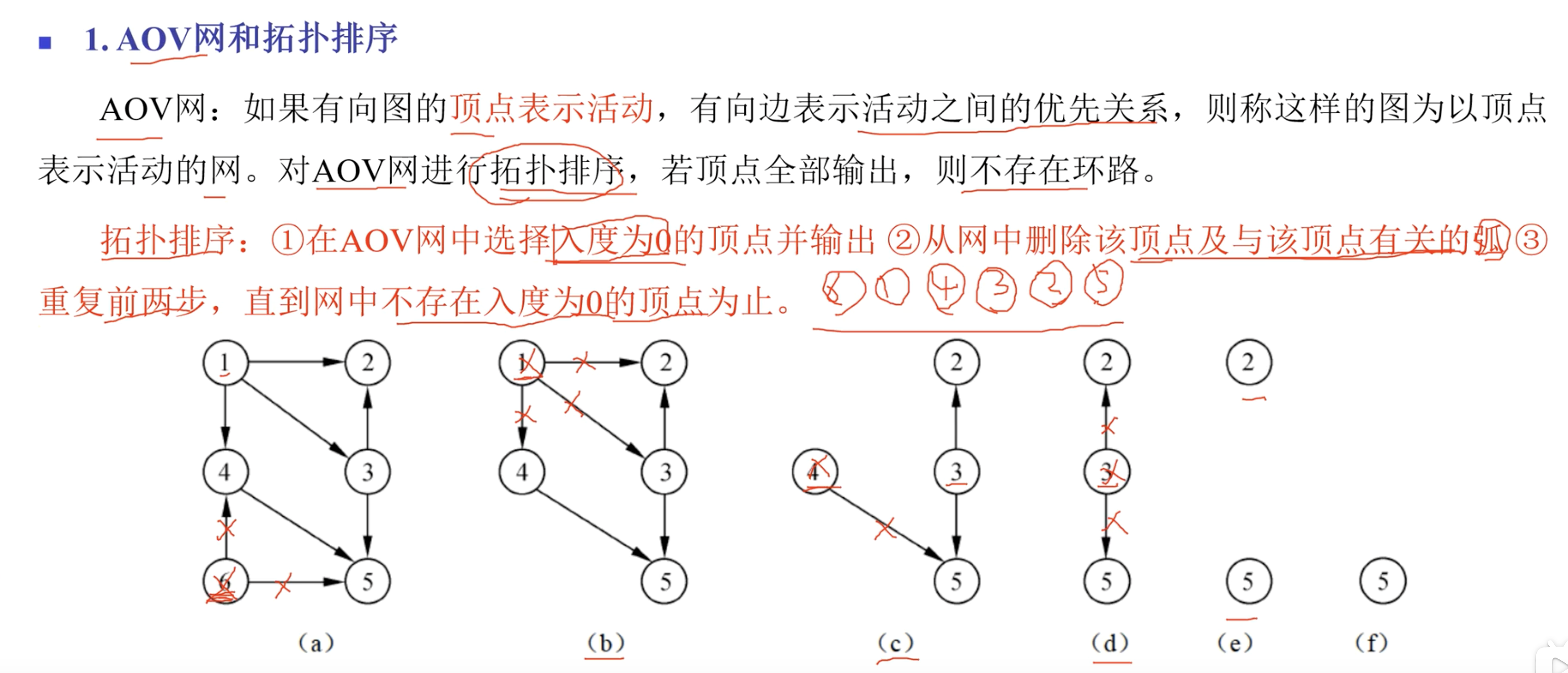
每次选择入度为0的节点,删除节点和与之相连边,直到不存在入度为0的顶点
注意:拓扑排序的顺序不一定唯一
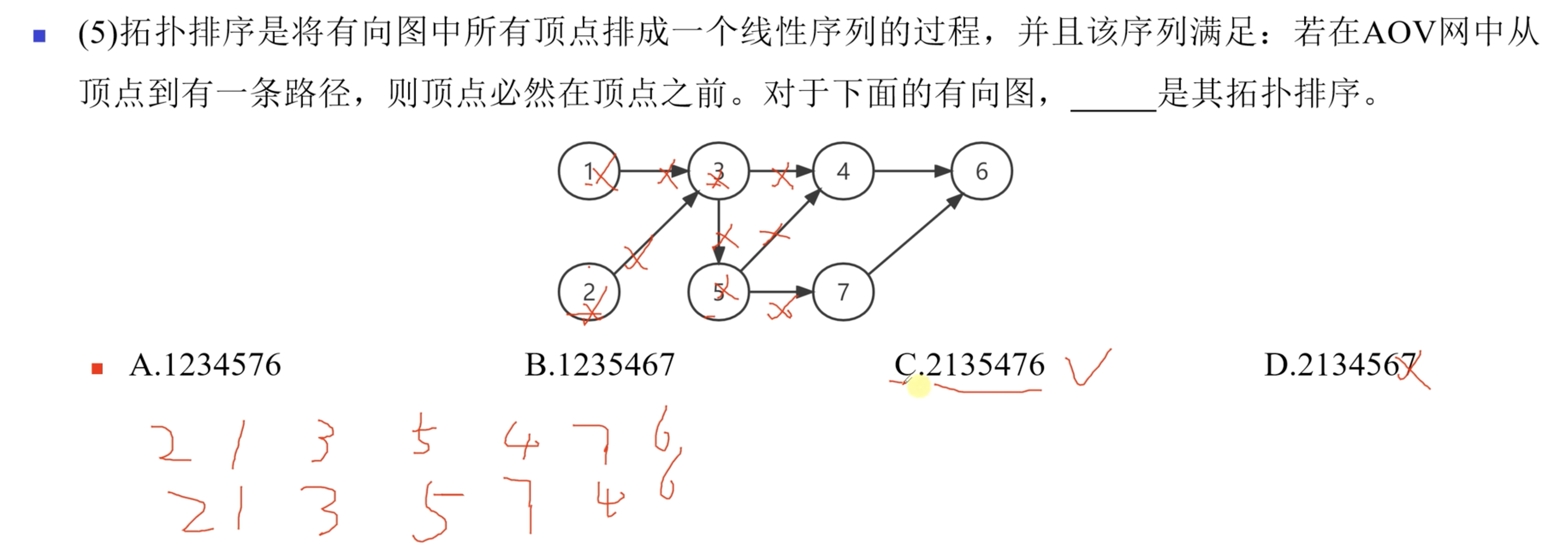
6. 关键路径

关键路径可能不唯一
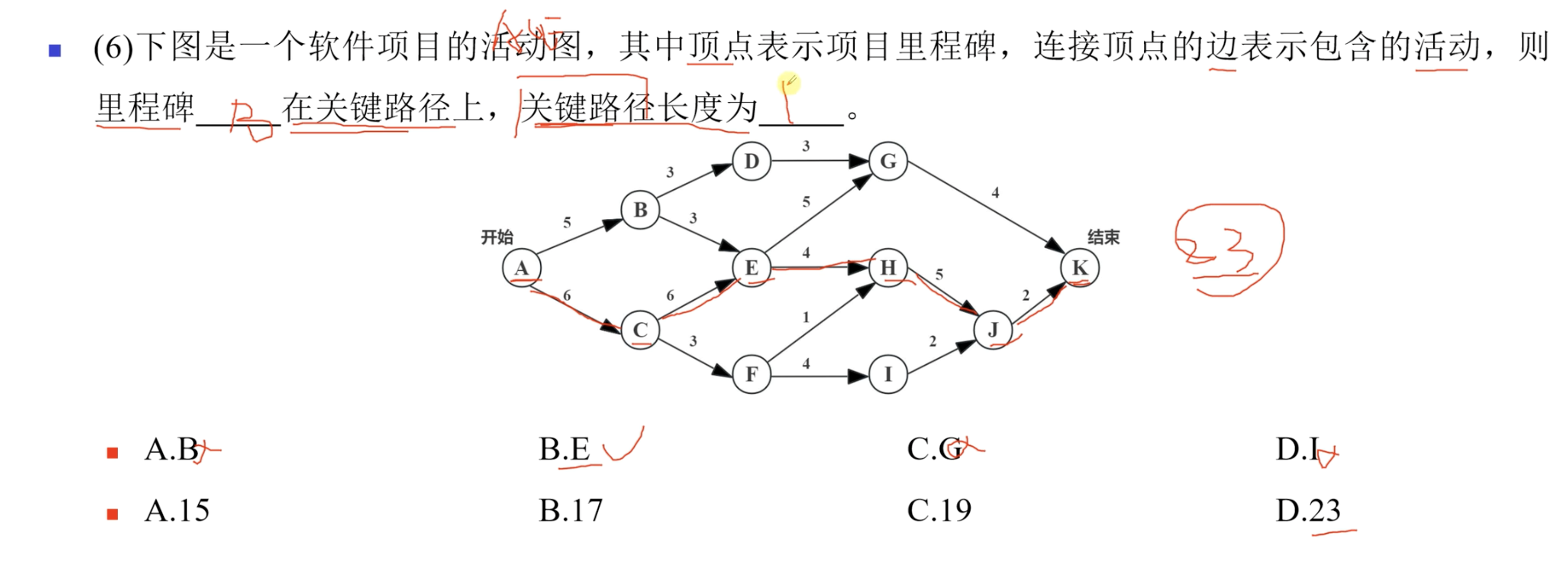
7. 最短路径
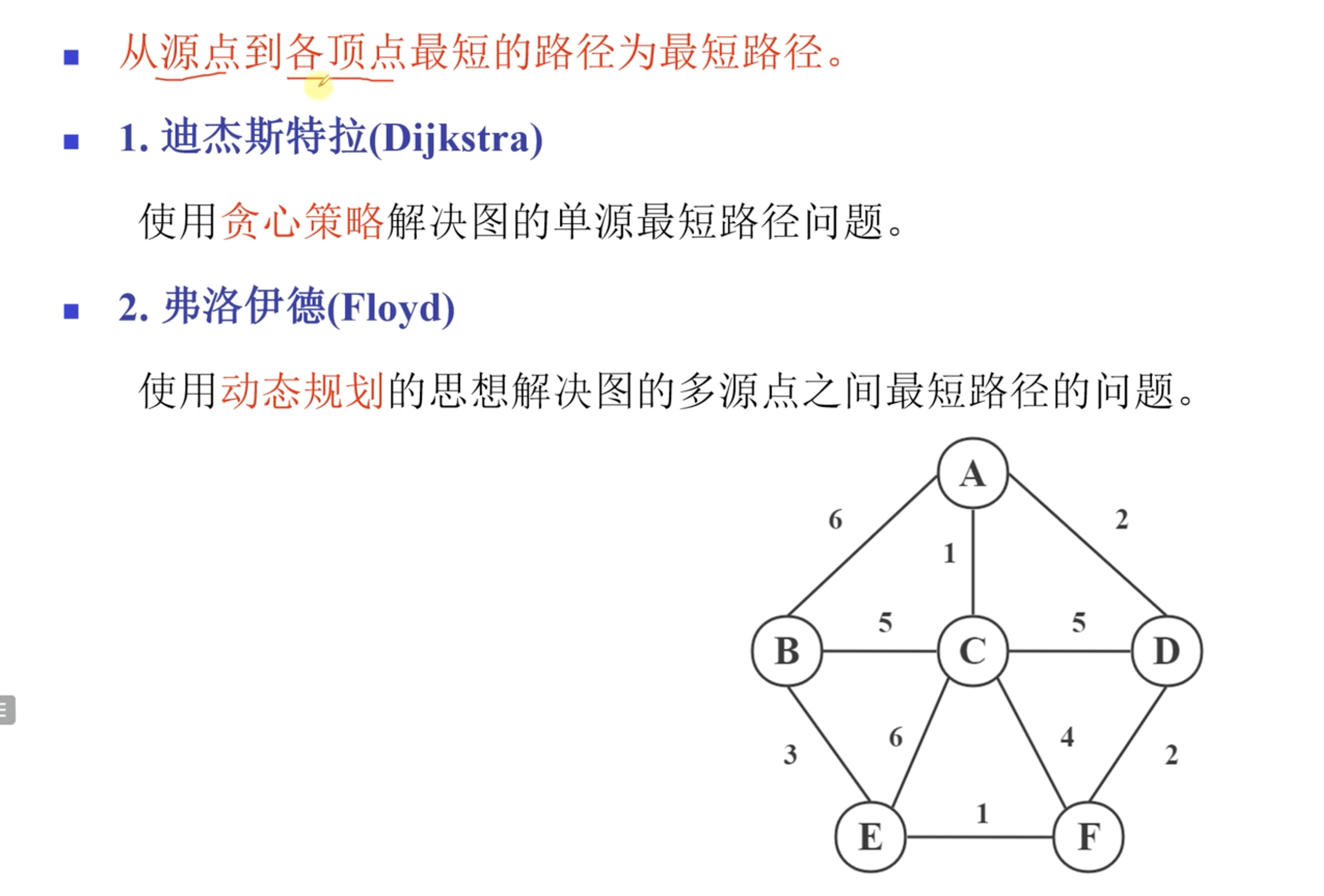
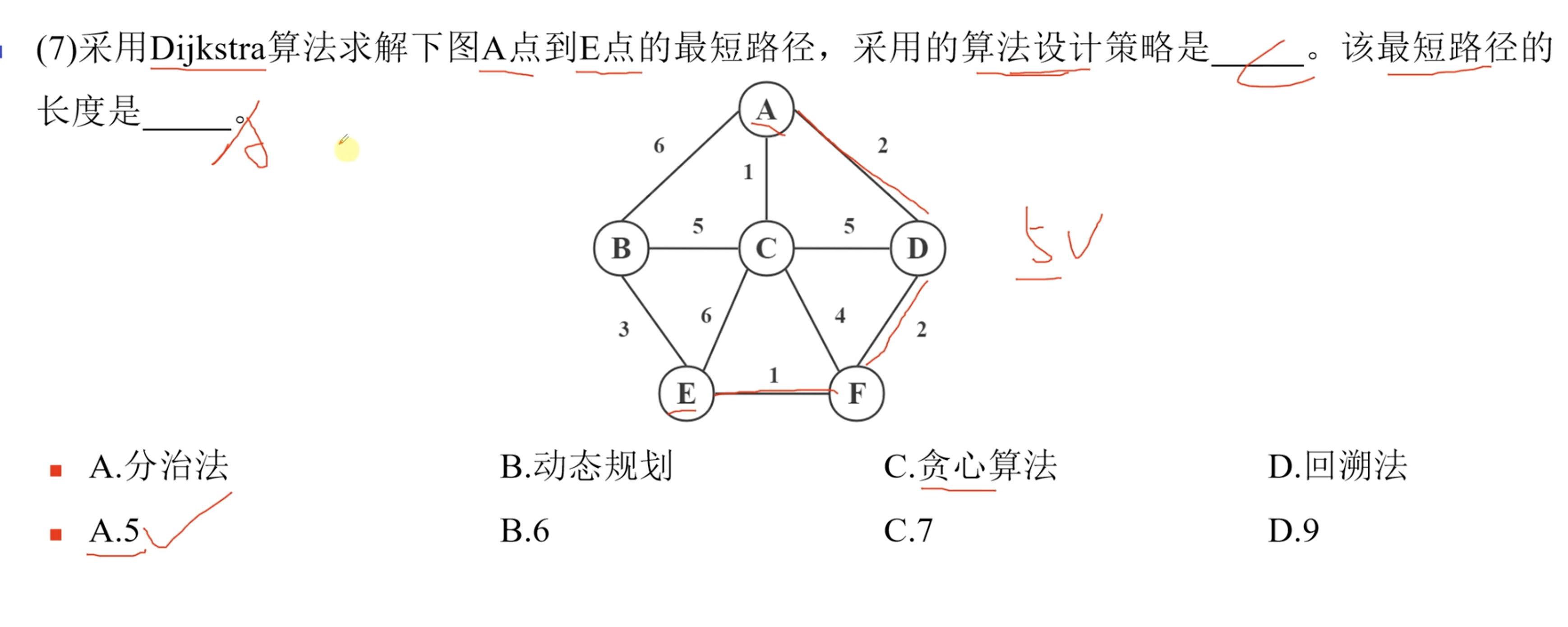
无需掌握这两种算法具体怎么计算的,考试的时候直接看图就可以找到两个顶点之间的最短路径