​​​​​​1806. 还原排列的最少操作步数

本题是数论题 共介绍4种解题方法

目录

1、所有置换环长度的最小公倍数

2、最小操作数是最大环长度

3、1或n-2所在环长度即为最大置换环长度

4、暴力模拟

---

思路：

因为数据范围很小 所以可以直接模拟

也可以优化一下——通过样例发现，最少操作数就是最大置换环的长度

更严谨地说，最少操作数 = 所有置换环长度的最小公倍数

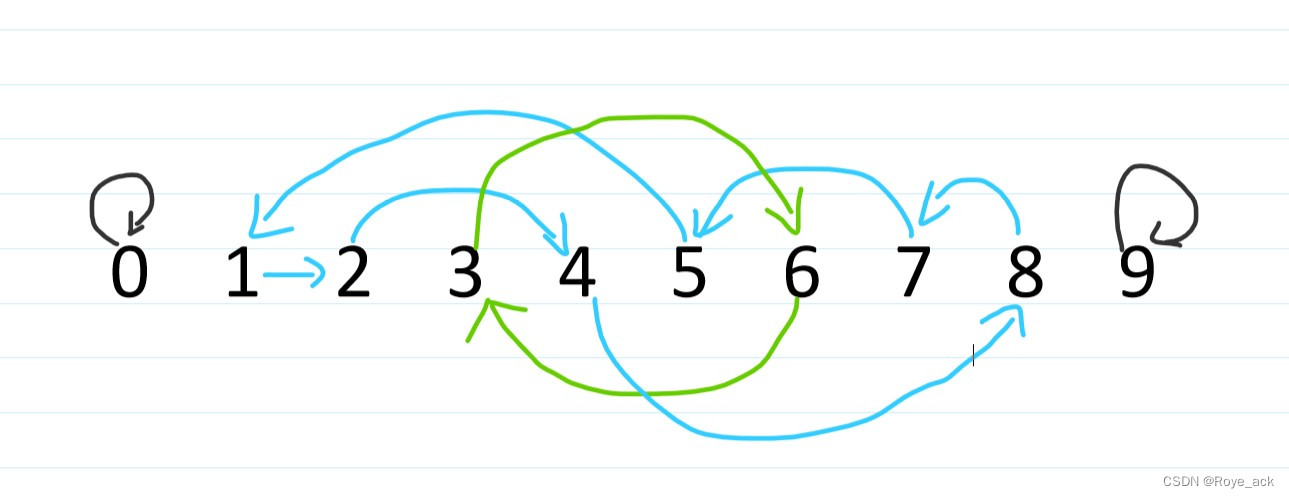
 比如上图，n=10

置换环1 ：【0】

置换环2 ：【1，2，4，8，7，5】 

置换环3：【3，6】

置换环4：【9】

所以我们可以找出所以环长度的最小公倍数就是最少操作数

1、所有置换环长度的最小公倍数

gcd最大公约数

int gcd(int a,int b)
{
    return b!=0? gcd(b,a%b):a;
}

lcm最小公倍数

int lcm=a*b/gcd(a,b);

class Solution {
public:
    int reinitializePermutation(int n) 
    {
        int res=1,cnt;
        for(int i=1;i<n-1;i++) //0和n-1永远是自环 长度为1 不用枚举
        {
            int j=i;
            cnt=0;
            vector<int> st(n,0);
            while(!st[j])
            {
                st[j]=1;
                cnt++;
                j= j&1? n/2+(j-1)/2:j/2;
            }
            res=lcm(res,cnt);
        }
        return res;
    }
};

2、最小操作数是最大环长度

class Solution {
public:
    int reinitializePermutation(int n) 
    {
        vector<int> st(n,0);
        int res=1,cnt;
        for(int i=1;i<n-1;i++) //0和n-1永远是自环 长度为1 不用枚举
        {
            int j=i;
            cnt=0;
            while(!st[j])
            {
                st[j]=1;
                cnt++;
                j= j&1? n/2+(j-1)/2:j/2;
            }
            res=max(res,cnt);
        }
        return res;
    }
};

3、1或n-2所在环长度即为最大置换环长度

通过样例不难发现，下标为1或n-2永远处于最长置换环，所以算出其所在环长度即可

class Solution {
public:
    int reinitializePermutation(int n) 
    {
        int idx=1,res=0;
        do
        {
            idx= idx&1? n/2+(idx-1)/2:idx/2;
            res++;
        }while(idx!=1);
        return res;
    }
};

class Solution {
public:
    int reinitializePermutation(int n) 
    {
        int idx=n-2,res=0;
        do
        {
            idx= idx&1? n/2+(idx-1)/2:idx/2;
            res++;
        }while(idx!=n-2);
        return res;
    }
};

 

4、暴力模拟

class Solution {
public:
    int reinitializePermutation(int n) {
        vector<int> p,t;
        vector<int> a(n,0);
        for(int i=0;i<n;i++) p.push_back(i),t.push_back(i);

        int res=0;
        while(1)
        {
            if(a==t) break;
            for(int i=0;i<n;i++)
            {
                if(i%2==0) a[i]=p[i/2];
                else a[i]=p[n/2+(i-1)/2];
            }
            res++;
            p=a;
        }
        return res;
    }
};