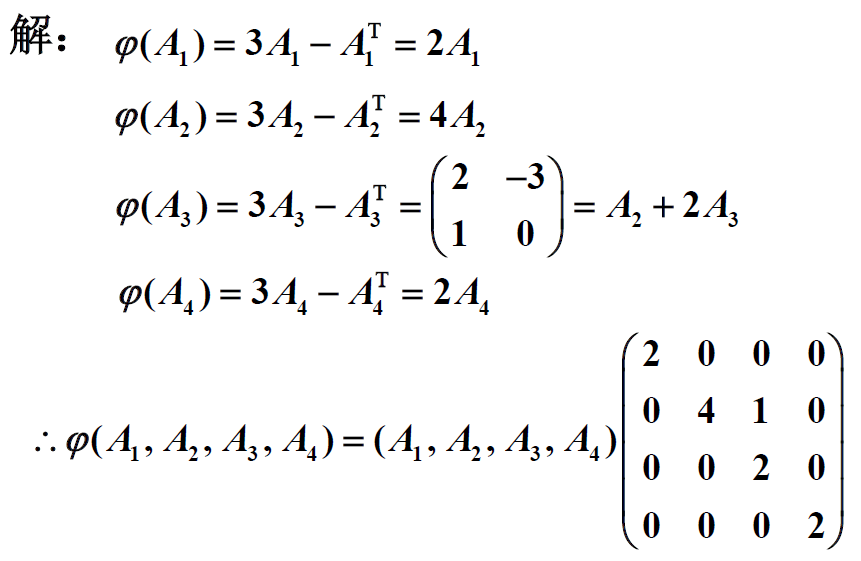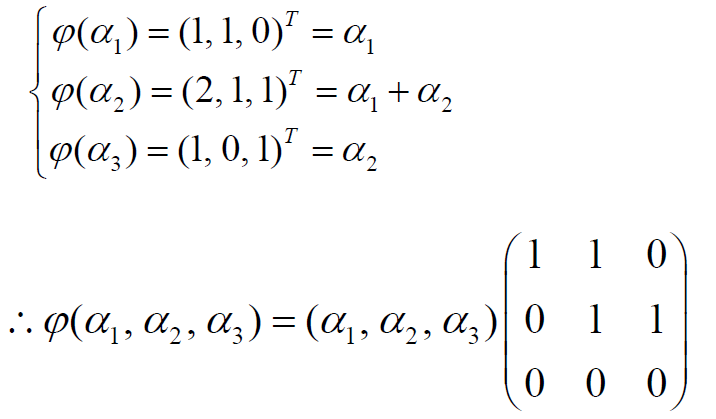矩阵论
1. 准备知识——复数域上矩阵,Hermite变换)
1.准备知识——复数域上的内积域正交阵
1.准备知识——Hermite阵,二次型,矩阵合同,正定阵,幂0阵,幂等阵,矩阵的秩
2. 矩阵分解——SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——正定阵分解
2. 矩阵分解——单阵谱分解
2. 矩阵分解——正规分解——正规阵
2. 矩阵分解——正规谱分解
2. 矩阵分解——高低分解
3. 矩阵函数——常见解析函数
3. 矩阵函数——谱公式,幂0与泰勒计算矩阵函数
3. 矩阵函数——矩阵函数求导
4. 矩阵运算——观察法求矩阵特征值特征向量
4. 矩阵运算——张量积
4. 矩阵运算——矩阵拉直
4.矩阵运算——广义逆——加号逆定义性质与特殊矩阵的加号逆
4. 矩阵运算——广义逆——加号逆的计算
4. 矩阵运算——广义逆——加号逆应用
4. 矩阵运算——广义逆——减号逆
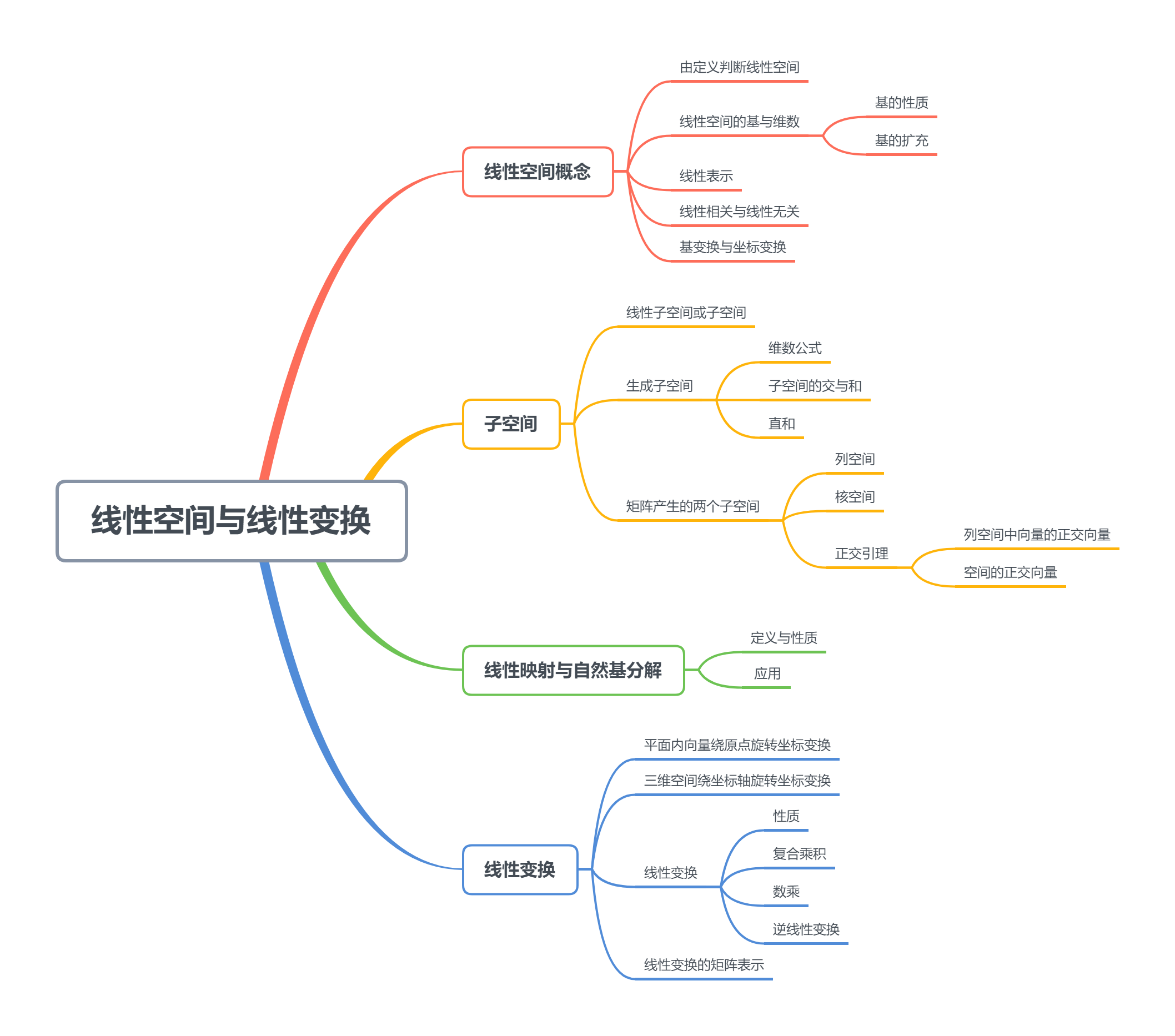
5. 线性空间与线性变换——线性空间
5. 线性空间与线性变换——生成子空间
5. 线性空间与线性变换——线性映射与自然基分解,线性变换
6. 正规方程与矩阵方程求解
7. 范数理论——基本概念——向量范数与矩阵范数
7.范数理论——基本概念——矩阵范数生成向量范数&谱范不等式
7. 矩阵理论——算子范数
7.范数理论——范数估计——许尔估计&谱估计
7. 范数理论——非负/正矩阵
8. 常用矩阵总结——秩1矩阵,优阵(单位正交阵),Hermite阵
8. 常用矩阵总结——镜面阵,正定阵
8. 常用矩阵总结——单阵,正规阵,幂0阵,幂等阵,循环阵
5.3 线性映射与自然基分解
同一空间——线性变换
不同空间——线性映射
自然基 :
R
n
R^n
Rn 中的自然基为:
ϵ
1
=
(
1
0
⋮
0
)
,
ϵ
2
=
(
0
1
⋮
0
)
,
⋯
,
ϵ
n
=
(
0
0
⋮
1
)
\epsilon_1=\left( \begin{matrix} 1\\0\\\vdots\\0 \end{matrix} \right),\epsilon_2=\left( \begin{matrix} 0\\1\\\vdots\\0 \end{matrix} \right),\cdots,\epsilon_n=\left( \begin{matrix} 0\\0\\\vdots\\1 \end{matrix} \right)
ϵ1=
10⋮0
,ϵ2=
01⋮0
,⋯,ϵn=
00⋮1
R
n
R^n
Rn 中每一向量
α
=
(
a
1
,
a
2
,
⋯
,
a
n
)
\alpha=(a_1,a_2,\cdots,a_n)
α=(a1,a2,⋯,an) 都有分解公式
α
=
a
1
ϵ
1
+
a
2
ϵ
2
+
⋯
+
a
n
ϵ
n
\alpha=a_1\epsilon_1+a_2\epsilon_2+\cdots+a_n\epsilon_n
α=a1ϵ1+a2ϵ2+⋯+anϵn
映射:设
S
S
S 和
S
′
S'
S′ 是两个集合,存在一个法则
σ
:
S
→
S
′
\sigma:S\rightarrow S'
σ:S→S′ ,它使
S
S
S 中的每个元素
a
a
a 在
S
′
S'
S′ 中有一个确定的元素
a
′
a'
a′ 与之对应,记为
σ
(
a
)
=
a
′
或
a
→
a
′
\sigma(a)=a' 或 a\rightarrow a'
σ(a)=a′或a→a′
称为集合
S
S
S 到
S
′
S'
S′ 的映射,
a
′
a'
a′ 称为
a
a
a 在映射
σ
\sigma
σ 下的 象 ,
a
a
a 为
a
′
a'
a′ 在映射
σ
\sigma
σ 下的 原象
交换: S S S 到 S S S 自身的映射
相等:设 σ 1 \sigma_1 σ1 与 σ 2 \sigma_2 σ2 都是集合 S S S 到 S ′ S' S′ 的映射,如果对于 ∀ a ∈ S \forall a\in S ∀a∈S ,都有 σ 1 ( a ) = σ 2 ( a ) \sigma_1(a)=\sigma_2(a) σ1(a)=σ2(a) ,则称 σ 1 \sigma_1 σ1 与 σ 2 \sigma_2 σ2 相等,记为 σ 1 = σ 2 \sigma_1=\sigma_2 σ1=σ2
乘法:设 σ \sigma σ , τ \tau τ 依次是集合 S S S 到 S 1 S_1 S1 , S 1 S_1 S1 到 S 2 S_2 S2 的映射 ,乘积 τ σ \tau \sigma τσ 定义为 ( τ σ ) ( a ) = Δ τ ( σ ( a ) ) , a ∈ S (\tau\sigma)(a)\overset{\Delta}{=}\tau(\sigma(a)),a\in S (τσ)(a)=Δτ(σ(a)),a∈S , τ σ \tau\sigma τσ 是 S S S 到 S 2 S_2 S2 的一个映射
- 不满足交换律: τ σ ≠ σ τ \tau\sigma\neq \sigma \tau τσ=στ
- 满足结合律: μ ( τ σ ) = ( μ τ ) σ \mu(\tau\sigma)=(\mu\tau)\sigma μ(τσ)=(μτ)σ ( μ \mu μ 是 S 2 S_2 S2 到 S 3 S_3 S3 的映射)
5.3.1 定义与性质
设
W
W
W 为一个线性空间,且
φ
:
W
→
R
n
\varphi:W\rightarrow R^n
φ:W→Rn 是一个映射
(
α
,
β
∈
W
,
k
∈
R
)
(\alpha,\beta\in W,k\in R)
(α,β∈W,k∈R) ,若满足:
(
1
)
φ
(
α
+
β
)
=
φ
(
α
)
+
φ
(
β
)
(
2
)
φ
(
k
α
)
=
k
φ
(
α
)
\begin{aligned} (1)&\varphi(\alpha+\beta)=\varphi(\alpha)+\varphi(\beta)\\ (2)&\varphi(k\alpha)=k\varphi(\alpha) \end{aligned}
(1)(2)φ(α+β)=φ(α)+φ(β)φ(kα)=kφ(α)
则称
φ
\varphi
φ 为
W
W
W 到
R
n
R^n
Rn 的一个线性映射
性质
零点不变: φ ( 0 ) = 0 \varphi(0)=0 φ(0)=0
线性映射保持线性组合结构 : φ ( k 1 α 1 + k 2 α 2 + ⋯ + k p α p ) = k 1 φ ( α 1 ) + k 2 φ ( α 2 ) + ⋯ + k p φ ( α p ) , k 1 , k 2 , ⋯ , k p ∈ R \varphi(k_1\alpha_1+k_2\alpha_2+\cdots+k_p\alpha_p)=k_1\varphi(\alpha_1)+k_2\varphi(\alpha_2)+\cdots+k_p\varphi(\alpha_p),k_1,k_2,\cdots,k_p\in R φ(k1α1+k2α2+⋯+kpαp)=k1φ(α1)+k2φ(α2)+⋯+kpφ(αp),k1,k2,⋯,kp∈R
原象线性相关(无关),则像也线性相关(无关)
5.3.2 应用
- 构造一个线性映射,把未知问题转化为求原象问题
- 写出自然基分解公式,然后找出自然基的原象
- 写出自然基原象的线性组合,可得所求原象

解:令多项式集合 W = { f ( x ) = a 0 + a 1 x + ⋯ + a n − 1 x n − 1 ∣ a j ∈ R , 0 ≤ j ≤ n − 1 } W=\{f(x)=a_0+a_1x+\cdots+a_{n-1}x^{n-1}\vert a_j\in R,0\le j\le n-1\} W={f(x)=a0+a1x+⋯+an−1xn−1∣aj∈R,0≤j≤n−1} , W W W 为一个线性空间, d i m ( W ) = n dim(W)=n dim(W)=n
引入映射
φ
:
W
→
R
n
,
∀
f
,
g
∈
W
\varphi:W\rightarrow R^n,\forall f,g\in W
φ:W→Rn,∀f,g∈W
φ
(
f
)
=
(
f
(
x
1
)
,
f
(
x
2
)
,
⋯
,
f
(
x
n
)
)
φ
(
g
)
=
(
g
(
x
1
)
,
g
(
x
2
)
,
⋯
,
g
(
x
n
)
)
\varphi(f)=(f(x_1),f(x_2),\cdots,f(x_n))\\ \varphi(g)=(g(x_1),g(x_2),\cdots,g(x_n))
φ(f)=(f(x1),f(x2),⋯,f(xn))φ(g)=(g(x1),g(x2),⋯,g(xn))
对于映射
φ
\varphi
φ ,有
φ
(
f
+
g
)
=
φ
(
f
)
+
φ
(
g
)
\varphi(f+g)=\varphi(f)+\varphi(g)
φ(f+g)=φ(f)+φ(g) ,
φ
(
k
f
)
=
k
φ
(
f
)
\varphi(kf)=k\varphi(f)
φ(kf)=kφ(f) ,可知
φ
\varphi
φ 为线性映射(不改变组合结构)
设 f ( x ) ∈ W f(x)\in W f(x)∈W 为所求的多项式,满足: f ( x 1 ) = b 1 , f ( x 2 ) = b 2 , ⋯ , f ( x n ) = b n f(x_1)=b_1,f(x_2)=b_2,\cdots,f(x_n)=b_n f(x1)=b1,f(x2)=b2,⋯,f(xn)=bn
令 β = ( b 1 , b 2 , ⋯ , b n ) ∈ R n \beta=(b_1,b_2,\cdots,b_n)\in R^n β=(b1,b2,⋯,bn)∈Rn ,则有 φ ( f ) = ( f ( x 1 ) , f ( x 2 ) , ⋯ , f ( x n ) ) = ( b 1 , b 2 , ⋯ , b n ) = β \varphi(f)=(f(x_1),f(x_2),\cdots,f(x_n))=(b_1,b_2,\cdots,b_n)=\beta φ(f)=(f(x1),f(x2),⋯,f(xn))=(b1,b2,⋯,bn)=β
即问题转化为求一个 f f f ,使 φ ( f ) = β = b 1 ϵ 1 + b 2 ϵ 2 + ⋯ + b n ϵ n \varphi(f)=\beta=b_1\epsilon_1+b_2\epsilon_2+\cdots+b_n\epsilon_n φ(f)=β=b1ϵ1+b2ϵ2+⋯+bnϵn ,其原象 f 1 , f 2 , ⋯ , f n ∈ W f_1,f_2,\cdots,f_n\in W f1,f2,⋯,fn∈W 使 φ ( f 1 ) = ϵ 1 , φ ( f 2 ) = ϵ 2 , ⋯ , φ ( f n ) = ϵ n \varphi(f_1)=\epsilon_1,\varphi(f_2)=\epsilon_2,\cdots,\varphi(f_n)=\epsilon_n φ(f1)=ϵ1,φ(f2)=ϵ2,⋯,φ(fn)=ϵn
则必有 φ ( f ) = b 1 φ ( f 1 ) + b 2 φ ( f 2 ) + ⋯ + b n φ ( f n ) = b 1 ϵ 1 + b 2 ϵ 2 + ⋯ + b n ϵ n = β \varphi(f)=b_1\varphi(f_1)+b_2\varphi(f_2)+\cdots+b_n\varphi(f_n)=b_1\epsilon_1+b_2\epsilon_2+\cdots+b_n\epsilon_n=\beta φ(f)=b1φ(f1)+b2φ(f2)+⋯+bnφ(fn)=b1ϵ1+b2ϵ2+⋯+bnϵn=β
若 φ ( f 1 ) = ϵ 1 = ( 1 , 0 , ⋯ , 0 ) ⇒ ( f 1 ( x 1 ) , f 1 ( x 2 ) , ⋯ , f n ( x n ) ) = ( 1 , 0 , ⋯ , 0 ) ⇒ f 1 ( x 1 ) = 1 , f 1 ( x 2 ) = ⋯ = f 1 ( x n ) = 0 \varphi(f_1)=\epsilon_1=(1,0,\cdots,0)\Rightarrow (f_1(x_1),f_1(x_2),\cdots,f_n(x_n))=(1,0,\cdots,0)\\\Rightarrow f_1(x_1)=1,f_1(x_2)=\cdots=f_1(x_n)=0 φ(f1)=ϵ1=(1,0,⋯,0)⇒(f1(x1),f1(x2),⋯,fn(xn))=(1,0,⋯,0)⇒f1(x1)=1,f1(x2)=⋯=f1(xn)=0
则
(
n
−
1
)
(n-1)
(n−1) 次多项式
f
1
f_1
f1 恰有
n
−
1
n-1
n−1 个根为
x
2
,
x
3
,
⋯
,
x
n
x_2,x_3,\cdots,x_n
x2,x3,⋯,xn ,可设
f
1
(
x
)
=
k
1
(
x
−
x
2
)
(
x
−
x
3
)
⋯
(
x
−
x
n
)
⇒
1
=
f
1
(
x
1
)
k
1
=
1
(
x
1
−
x
2
)
(
x
1
−
x
3
)
⋯
(
x
1
−
x
n
)
⇒
f
1
(
x
)
=
(
x
−
x
2
)
(
x
−
x
3
)
⋯
(
x
−
x
n
)
(
x
1
−
x
2
)
(
x
1
−
x
3
)
⋯
(
x
1
−
x
n
)
\begin{aligned} &f_1(x)=k_1(x-x_2)(x-x_3)\cdots(x-x_n)\\ &\xRightarrow{1=f_1(x_1)}k_1=\frac{1}{(x_1-x_2)(x_1-x_3)\cdots(x_1-x_n)} \\ &\Rightarrow f_1(x)=\frac{(x-x_2)(x-x_3)\cdots(x-x_n)}{(x_1-x_2)(x_1-x_3)\cdots(x_1-x_n)} \end{aligned}
f1(x)=k1(x−x2)(x−x3)⋯(x−xn)1=f1(x1)k1=(x1−x2)(x1−x3)⋯(x1−xn)1⇒f1(x)=(x1−x2)(x1−x3)⋯(x1−xn)(x−x2)(x−x3)⋯(x−xn)
同理:
f
(
x
)
=
b
1
f
1
(
x
)
+
b
2
f
2
(
x
)
+
⋯
+
b
n
f
n
(
x
)
f
1
(
x
)
=
(
x
−
x
2
)
(
x
−
x
3
)
⋯
(
x
−
x
n
)
(
x
1
−
x
2
)
(
x
1
−
x
3
)
⋯
(
x
1
−
x
n
)
f
2
(
x
)
=
(
x
−
x
1
)
(
x
−
x
2
)
⋯
(
x
−
x
n
)
(
x
2
−
x
1
)
(
x
2
−
x
3
)
⋯
(
x
2
−
x
n
)
⋮
f
n
(
x
)
=
(
x
−
x
1
)
(
x
−
x
2
)
⋯
(
x
−
x
n
−
1
)
(
x
n
−
x
1
)
(
x
n
−
x
2
)
⋯
(
x
n
−
x
n
−
1
)
\begin{aligned} &f(x)=b_1f_1(x)+b_2f_2(x)+\cdots+b_nf_n(x)\\ &f_1(x)=\frac{(x-x_2)(x-x_3)\cdots(x-x_n)}{(x_1-x_2)(x_1-x_3)\cdots(x_1-x_n)}\\ &f_2(x)=\frac{(x-x_1)(x-x_2)\cdots(x-x_n)}{(x_2-x_1)(x_2-x_3)\cdots(x_2-x_n)}\\ &\vdots\\ &f_n(x)=\frac{(x-x_1)(x-x_2)\cdots(x-x_{n-1})}{(x_n-x_1)(x_n-x_2)\cdots(x_n-x_{n-1})} \end{aligned}
f(x)=b1f1(x)+b2f2(x)+⋯+bnfn(x)f1(x)=(x1−x2)(x1−x3)⋯(x1−xn)(x−x2)(x−x3)⋯(x−xn)f2(x)=(x2−x1)(x2−x3)⋯(x2−xn)(x−x1)(x−x2)⋯(x−xn)⋮fn(x)=(xn−x1)(xn−x2)⋯(xn−xn−1)(x−x1)(x−x2)⋯(x−xn−1)
eg


由 φ ( f ) = ( f ( x 1 ) , f ( x 2 ) , ⋯ , f ( x n ) ) ∈ R n ,可知 φ ( f 1 ) = ϵ 1 , φ ( f 2 ) = ϵ 2 , ⋯ , φ ( f n ) = ϵ n 由于 ϵ 1 , ⋯ , ϵ n 线性无关,由线性映射可知, f 1 , f 2 , ⋯ , f n 线性无关,任取 f ( x ) ∈ W ,则 f = k 1 f 1 + k 2 f 2 + ⋯ + k n f n 由 φ ( f ) = k 1 φ ( f 1 ) + k 2 φ ( f 2 ) + ⋯ + k n φ ( f n ) = k 1 ϵ 1 + k 2 ϵ 2 + ⋯ + k n ϵ n = ( k 1 , k 2 , ⋯ , k n ) ⇒ ( f ( x 1 ) , f ( x 2 ) , ⋯ , f ( x n ) ) = ( ϵ 1 , ϵ 2 , ⋯ , ϵ n ) ⇒ k 1 = f ( x 1 ) , k 2 = f ( x 2 ) , ⋯ , k n = f ( x n ) ⇒ f ( x ) = f ( x 1 ) f 1 ( x ) + f ( x 2 ) f 2 ( x ) + ⋯ + f ( x n ) f n ( x ) \begin{aligned} &由 \varphi(f)=(f(x_1),f(x_2),\cdots,f(x_n))\in R^n,可知\varphi(f_1)=\epsilon_1,\varphi(f_2)=\epsilon_2,\cdots,\varphi(f_n)=\epsilon_n\\ &由于 \epsilon_1,\cdots,\epsilon_n线性无关,由线性映射可知,f_1,f_2,\cdots,f_n线性无关,任取f(x)\in W,则\\ &f=k_1f_1+k_2f_2+\cdots+k_nf_n\\ &由\varphi(f)=k_1\varphi(f_1)+k_2\varphi(f_2) +\cdots+k_n\varphi(f_n)=k_1\epsilon_1+k_2\epsilon_2+\cdots+k_n\epsilon_n=(k_1,k_2,\cdots,k_n)\\ &\Rightarrow (f(x_1),f(x_2),\cdots,f(x_n))=(\epsilon_1,\epsilon_2,\cdots,\epsilon_n)\\ &\Rightarrow k_1=f(x_1),k_2=f(x_2),\cdots,k_n=f(x_n)\\ &\Rightarrow f(x)=f(x_1)f_1(x)+f(x_2)f_2(x)+\cdots+f(x_n)f_n(x) \end{aligned} 由φ(f)=(f(x1),f(x2),⋯,f(xn))∈Rn,可知φ(f1)=ϵ1,φ(f2)=ϵ2,⋯,φ(fn)=ϵn由于ϵ1,⋯,ϵn线性无关,由线性映射可知,f1,f2,⋯,fn线性无关,任取f(x)∈W,则f=k1f1+k2f2+⋯+knfn由φ(f)=k1φ(f1)+k2φ(f2)+⋯+knφ(fn)=k1ϵ1+k2ϵ2+⋯+knϵn=(k1,k2,⋯,kn)⇒(f(x1),f(x2),⋯,f(xn))=(ϵ1,ϵ2,⋯,ϵn)⇒k1=f(x1),k2=f(x2),⋯,kn=f(xn)⇒f(x)=f(x1)f1(x)+f(x2)f2(x)+⋯+f(xn)fn(x)
5.4 线性变换
5.4.1 平面内向量绕原点旋转坐标变换
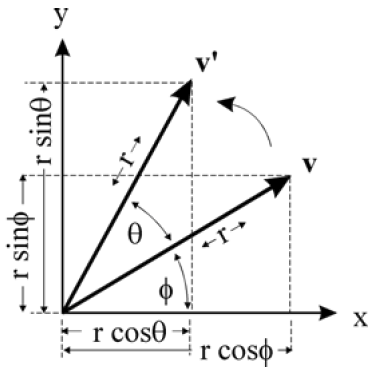
设向量 V = ( x y ) V=\left(\begin{matrix}x\\y\end{matrix}\right) V=(xy) 旋转 θ \theta θ 角后变为 V ′ = ( x ′ y ′ ) V'=\left(\begin{matrix}x'\\y'\end{matrix}\right) V′=(x′y′) , V V V 的倾角为 φ \varphi φ
可写
x
=
r
c
o
s
φ
,
y
=
r
s
i
n
φ
{
x
′
=
r
c
o
s
(
θ
+
φ
)
=
r
c
o
s
θ
c
o
s
φ
−
r
s
i
n
θ
s
i
n
φ
y
′
=
r
s
i
n
(
θ
+
φ
)
=
r
s
i
n
θ
c
o
s
φ
+
r
c
o
s
θ
s
i
n
φ
⟺
{
x
′
=
x
c
o
s
θ
−
y
s
i
n
θ
y
′
=
x
s
i
n
θ
+
y
c
o
s
θ
令
A
=
(
c
o
s
θ
−
s
i
n
θ
s
i
n
θ
c
o
s
θ
)
,
可写
(
x
′
y
′
)
=
(
c
o
s
θ
−
s
i
n
θ
s
i
n
θ
c
o
s
θ
)
(
x
y
)
=
A
(
x
y
)
\begin{aligned} &x=rcos\varphi,y=rsin\varphi\\ &\left\{ \begin{aligned} &x'=rcos(\theta+\varphi)=rcos\theta cos\varphi-rsin\theta sin\varphi\\ &y'=rsin(\theta+\varphi)=rsin\theta cos\varphi+rcos\theta sin\varphi \end{aligned} \right.\\ &\iff\left\{ \begin{aligned} x'=xcos\theta-ysin\theta\\ y'=xsin\theta+ycos\theta \end{aligned} \right.\\ &令A=\left( \begin{matrix} cos\theta&-sin\theta\\ sin\theta&cos\theta \end{matrix} \right),可写\left( \begin{matrix} x'\\y' \end{matrix} \right)=\left( \begin{matrix} cos\theta&-sin\theta\\sin\theta&cos\theta \end{matrix} \right)\left( \begin{matrix} x\\y \end{matrix} \right)=A\left( \begin{matrix} x\\y \end{matrix} \right) \end{aligned}
x=rcosφ,y=rsinφ{x′=rcos(θ+φ)=rcosθcosφ−rsinθsinφy′=rsin(θ+φ)=rsinθcosφ+rcosθsinφ⟺{x′=xcosθ−ysinθy′=xsinθ+ycosθ令A=(cosθsinθ−sinθcosθ),可写(x′y′)=(cosθsinθ−sinθcosθ)(xy)=A(xy)
5.4.2 三维空间绕坐标轴旋转坐标变换
a. 绕z轴旋转
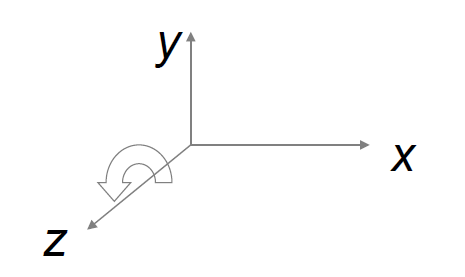
{ x ′ = x c o s φ − y s i n φ y ′ = x s i n φ + y c o s φ z ′ = z , φ 为 V 与 V ′ 在 x o y 面投影的夹角 记为 ( x ′ y ′ z ′ ) = ( c o s φ − s i n φ 0 s i n φ c o s φ 0 0 0 1 ) ( x y z ) \begin{aligned} &\left\{ \begin{aligned} &x'=xcos\varphi-ysin\varphi\\ &y'=xsin\varphi+ycos\varphi\\ &z'=z \end{aligned} \right.\quad,\varphi为V与V'在xoy面投影的夹角\\ &记为\left( \begin{matrix} x'\\y'\\z' \end{matrix} \right)=\left( \begin{matrix} cos\varphi&-sin\varphi&0\\ sin\varphi&cos\varphi&0\\ 0&0&1 \end{matrix} \right)\left( \begin{matrix} x\\y\\z \end{matrix} \right) \end{aligned} ⎩ ⎨ ⎧x′=xcosφ−ysinφy′=xsinφ+ycosφz′=z,φ为V与V′在xoy面投影的夹角记为 x′y′z′ = cosφsinφ0−sinφcosφ0001 xyz
b. 绕x轴旋转
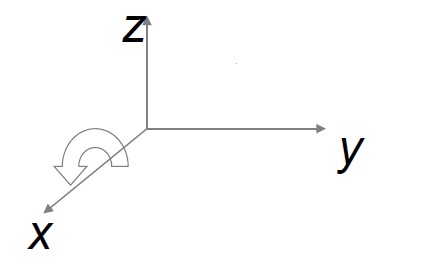
{ x ′ = x y ′ = y c o s α − z s i n α z ′ = y s i n α + z c o s α , α 为 V 与 V ′ 在 z o y 面投影的夹角 记为 ( x ′ y ′ z ′ ) = ( 1 0 0 0 c o s α − s i n α 0 s i n α c o s α ) ( x y z ) \begin{aligned} &\left\{ \begin{aligned} &x'=x\\ &y'=ycos\alpha-zsin\alpha\\ &z'=ysin\alpha+zcos\alpha \end{aligned} \right.\quad,\alpha为V与V'在zoy面投影的夹角\\ &记为\left( \begin{matrix} x'\\y'\\z' \end{matrix} \right)=\left( \begin{matrix} 1&0&0\\ 0&cos\alpha&-sin\alpha\\ 0&sin\alpha&cos\alpha\\ \end{matrix} \right)\left( \begin{matrix} x\\y\\z \end{matrix} \right) \end{aligned} ⎩ ⎨ ⎧x′=xy′=ycosα−zsinαz′=ysinα+zcosα,α为V与V′在zoy面投影的夹角记为 x′y′z′ = 1000cosαsinα0−sinαcosα xyz
c. 绕y轴旋转
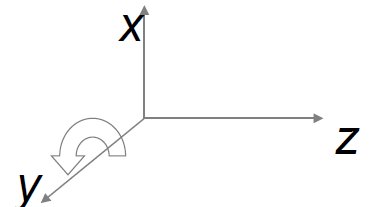
{ y ′ = y z ′ = z c o s β − x s i n β x ′ = z s i n β + x c o s β , β 为 V 与 V ′ 在 x o z 面投影的夹角 记为 ( x ′ y ′ z ′ ) = ( c o s β 0 s i n β 0 1 0 − s i n β 0 c o s β ) ( x y z ) \begin{aligned} &\left\{ \begin{aligned} &y'=y\\ &z'=zcos\beta-xsin\beta\\ &x'=zsin\beta+xcos\beta\\ \end{aligned} \right.\quad,\beta为V与V'在xoz面投影的夹角\\ &记为\left( \begin{matrix} x'\\y'\\z' \end{matrix} \right)=\left( \begin{matrix} cos\beta&0&sin\beta\\ 0&1&0\\ -sin\beta&0&cos\beta\\ \end{matrix} \right)\left( \begin{matrix} x\\y\\z \end{matrix} \right) \end{aligned} ⎩ ⎨ ⎧y′=yz′=zcosβ−xsinβx′=zsinβ+xcosβ,β为V与V′在xoz面投影的夹角记为 x′y′z′ = cosβ0−sinβ010sinβ0cosβ xyz
5.4.3 线性变换
设
V
V
V 为数域
K
K
K 上的线性空间,若变换
σ
:
V
→
V
\sigma:V\rightarrow V
σ:V→V ,对于
∀
α
,
β
∈
V
,
k
∈
K
\forall \alpha,\beta\in V,k\in K
∀α,β∈V,k∈K ,满足
σ
(
α
+
β
)
=
σ
(
α
)
+
σ
(
β
)
σ
(
k
α
)
=
k
σ
(
α
)
\sigma(\alpha+\beta)=\sigma(\alpha)+\sigma(\beta)\\ \sigma(k\alpha)=k\sigma(\alpha)
σ(α+β)=σ(α)+σ(β)σ(kα)=kσ(α)
则称
σ
\sigma
σ 为空间
V
V
V 上的线性变换
a. 性质
-
σ \sigma σ 为 V V V 的线性变换,则 σ ( 0 ) = 0 \sigma(0)=0 σ(0)=0 , σ ( − α ) = − σ ( α ) \sigma(-\alpha)=-\sigma(\alpha) σ(−α)=−σ(α)
-
线性变换保持线性组合及关系式不变
若 β = k 1 α 1 + k 2 α 2 + ⋯ + k r α r \beta=k_1\alpha_1+k_2\alpha_2+\cdots+k_r\alpha_r β=k1α1+k2α2+⋯+krαr ,则 σ ( β ) = k 1 σ ( α 1 ) + k 2 σ ( α 2 ) + ⋯ + k r σ ( α r ) \sigma(\beta)=k_1\sigma(\alpha_1)+k_2\sigma(\alpha_2)+\cdots+k_r\sigma(\alpha_r) σ(β)=k1σ(α1)+k2σ(α2)+⋯+krσ(αr)
-
线性变换不改变线性相关性,但不保持线性无关性。即
若 α 1 , α 2 , ⋯ , α r \alpha_1,\alpha_2,\cdots,\alpha_r α1,α2,⋯,αr 线性相关,则 σ ( α 1 ) , σ ( α 2 ) , ⋯ , σ ( α r ) \sigma(\alpha_1),\sigma(\alpha_2),\cdots,\sigma(\alpha_r) σ(α1),σ(α2),⋯,σ(αr) 线性相关
若 α 1 , α 2 , ⋯ , α r \alpha_1,\alpha_2,\cdots,\alpha_r α1,α2,⋯,αr 线性无关,则 σ ( α 1 ) , σ ( α 2 ) , ⋯ , σ ( α r ) \sigma(\alpha_1),\sigma(\alpha_2),\cdots,\sigma(\alpha_r) σ(α1),σ(α2),⋯,σ(αr) 未必无关
b. 复合乘积
设 σ \sigma σ , τ \tau τ 为线性空间 V V V 的两个线性变换,复合乘积为 σ τ \sigma\tau στ : ( σ τ ) ( α ) = σ ( τ ( α ) ) , ∀ α ∈ V (\sigma\tau)(\alpha)=\sigma(\tau(\alpha)),\forall \alpha\in V (στ)(α)=σ(τ(α)),∀α∈V ,则 σ τ \sigma\tau στ 也是 V V V 上的线性变换
- 结合律: ( σ τ ) φ = σ ( τ φ ) (\sigma\tau)\varphi=\sigma(\tau\varphi) (στ)φ=σ(τφ)
- I σ = σ I = σ I\sigma=\sigma I=\sigma Iσ=σI=σ , I I I 为恒等变换
c. 数乘
设 σ \sigma σ 为空间 V V V 的线性变换,定义 k k k 与 σ \sigma σ 的数乘: ( k σ ) ( x ) = k σ ( x ) , ∀ x ∈ V (k\sigma)(x)=k\sigma(x),\forall x\in V (kσ)(x)=kσ(x),∀x∈V ,则 k σ k\sigma kσ 也是 V V V 的线性变换
性质:

d. 逆线性变换
设 σ \sigma σ 为空间 V V V 的线性变换,若有 V V V 的变换 τ \tau τ 使 σ τ = τ σ = I \sigma\tau=\tau\sigma=I στ=τσ=I ,则称 σ \sigma σ 为可逆变换, τ \tau τ 为 σ \sigma σ 的逆变换,记为 σ − 1 \sigma^{-1} σ−1
- 可逆变换 σ \sigma σ 的逆变换 σ − 1 \sigma^{-1} σ−1 也是线性变换
- 线性变换 σ \sigma σ 可逆 ⟺ \iff ⟺ 线性变换 σ \sigma σ 是一一对应的
- 设 ϵ 1 , ϵ 2 , ⋯ , ϵ n \epsilon_1,\epsilon_2,\cdots,\epsilon_n ϵ1,ϵ2,⋯,ϵn 是线性空间 V V V 的一组基, σ \sigma σ 为 V V V 的线性变换,则 σ \sigma σ 可逆当且仅当 σ ( ϵ 1 ) , ⋯ , σ ( ϵ n ) \sigma(\epsilon_1),\cdots,\sigma(\epsilon_n) σ(ϵ1),⋯,σ(ϵn) 线性无关
- 可逆线性变换是把 无关向量变成无关向量
5.4.4 线性变换的矩阵表示
设
ϵ
1
,
ϵ
2
,
⋯
,
ϵ
n
\epsilon_1,\epsilon_2,\cdots,\epsilon_n
ϵ1,ϵ2,⋯,ϵn 为数域
F
F
F 上线性空间
V
V
V 的一组基,
σ
\sigma
σ 为
V
V
V 的线性变换,基向量的像可被基线性表示,即
{
σ
(
ϵ
1
)
=
a
11
ϵ
1
+
a
21
ϵ
2
+
⋯
+
a
n
1
ϵ
n
σ
(
ϵ
2
)
=
a
12
ϵ
1
+
a
22
ϵ
2
+
⋯
+
a
n
2
ϵ
n
⋮
σ
(
ϵ
n
)
=
a
1
n
ϵ
1
+
a
2
n
ϵ
2
+
⋯
+
a
n
n
ϵ
n
\left\{ \begin{aligned} &\sigma(\epsilon_1)=a_{11}\epsilon_1+a_{21}\epsilon_{2}+\cdots+a_{n1}\epsilon_n\\ &\sigma(\epsilon_2)=a_{12}\epsilon_1+a_{22}\epsilon_{2}+\cdots+a_{n2}\epsilon_n\\ \vdots\\ &\sigma(\epsilon_n)=a_{1n}\epsilon_1+a_{2n}\epsilon_{2}+\cdots+a_{nn}\epsilon_n\\ \end{aligned} \right.
⎩
⎨
⎧⋮σ(ϵ1)=a11ϵ1+a21ϵ2+⋯+an1ϵnσ(ϵ2)=a12ϵ1+a22ϵ2+⋯+an2ϵnσ(ϵn)=a1nϵ1+a2nϵ2+⋯+annϵn
σ
(
ϵ
1
,
ϵ
2
,
⋯
,
ϵ
n
)
=
(
ϵ
1
,
ϵ
2
,
⋯
,
ϵ
n
)
A
\sigma(\epsilon_1,\epsilon_2,\cdots,\epsilon_n)=(\epsilon_1,\epsilon_2,\cdots,\epsilon_n)A
σ(ϵ1,ϵ2,⋯,ϵn)=(ϵ1,ϵ2,⋯,ϵn)A ,其中
A
=
(
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋮
⋮
⋱
⋮
a
n
1
a
n
2
⋯
a
n
n
)
A=\left(\begin{matrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{matrix}\right)
A=
a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann
矩阵 A A A 为线性变换 σ \sigma σ 在基 ϵ 1 , ϵ 2 , ⋯ , ϵ n \epsilon_1,\epsilon_2,\cdots,\epsilon_n ϵ1,ϵ2,⋯,ϵn 下的矩阵
定理:
设 ϵ 1 , ϵ 2 , ⋯ , ϵ n \epsilon_1,\epsilon_2,\cdots,\epsilon_n ϵ1,ϵ2,⋯,ϵn 为数域 F F F 上线性空间 V V V 的一组基,在这组基下, V V V 的每一个线性变换都与 F n × n F^{n\times n} Fn×n 中的唯一矩阵对应,且具有性质:
- 线性变换的和对应于矩阵的和
- 线性变换的乘积对应于矩阵的乘积
- 线性变换的数量积对应于矩阵的数量积
- 可逆线性变换与可逆矩阵对应,且逆变换对应于逆矩阵
设线性空间 V V V 上的线性变换 φ \varphi φ 在两个基 ϵ 1 , ϵ 2 , ⋯ , ϵ n \epsilon_1,\epsilon_2,\cdots,\epsilon_n ϵ1,ϵ2,⋯,ϵn 与 η 1 , η 2 , ⋯ , η n \eta_1,\eta_2,\cdots,\eta_n η1,η2,⋯,ηn 下的矩阵分别是 A A A 、 B B B ,则有相似公式 B = P − 1 A P B=P^{-1}AP B=P−1AP

eg