225. 用队列实现栈 - 力扣（LeetCode）

官方题解：https://leetcode.cn/problems/implement-stack-using-queues/solutions/432204/yong-dui-lie-shi-xian-zhan-by-leetcode-solution/

首先我们要知道

栈是一种后进先出的数据结构，元素从顶端入栈，然后从顶端出栈。

队列是一种先进先出的数据结构，元素从后端入队，然后从前端出队。

这题要求:

typedef struct {
    
} MyStack;


MyStack* myStackCreate() {
    
}

void myStackPush(MyStack* obj, int x) {
    
}

int myStackPop(MyStack* obj) {
    
}

int myStackTop(MyStack* obj) {
    
}

bool myStackEmpty(MyStack* obj) {
    
}

void myStackFree(MyStack* obj) {
    
}

/**
 * Your MyStack struct will be instantiated and called as such:
 * MyStack* obj = myStackCreate();
 * myStackPush(obj, x);
 
 * int param_2 = myStackPop(obj);
 
 * int param_3 = myStackTop(obj);
 
 * bool param_4 = myStackEmpty(obj);
 
 * myStackFree(obj);
*/

这里我们将用两种方法来完成这个问题:
 

方法一：两个队列

这个思路类似我们前面的用栈实现队列

我们的思路如下:

我们先创建两个队列,命名为queue1和queue2，queue1用于存储栈内的元素，queue2作为入栈操作的辅助队列。

入栈操作时，首先将元素入队到 queue2，然后将 queue1的全部元素依次出队并入队到 queue2，此时 queue2的前端的元素即为新入栈的元素，再将queue1和queue2互换，则queue1的元素即为栈内的元素，queue1的前端和后端分别对应栈顶和栈底。

​

假设此时push入队列一个2：

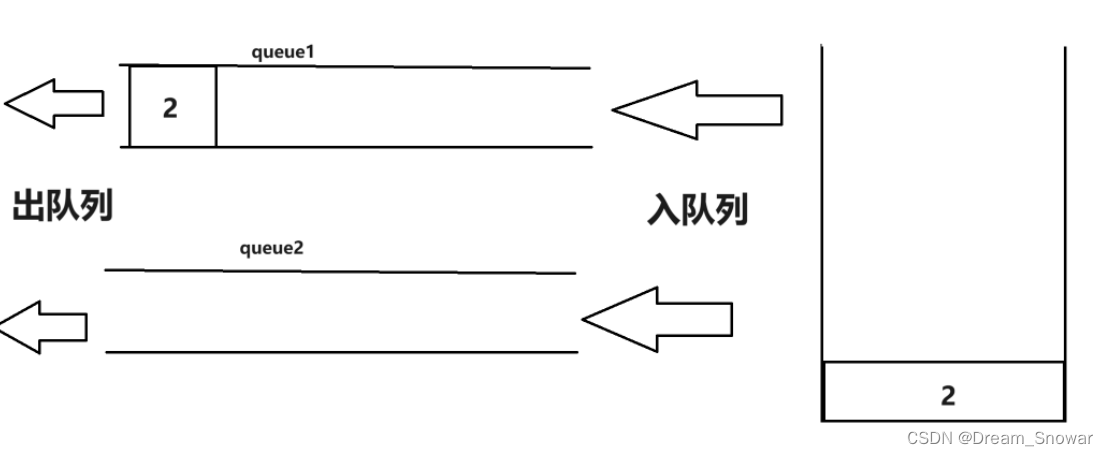
然后我们再push一个3入队列：

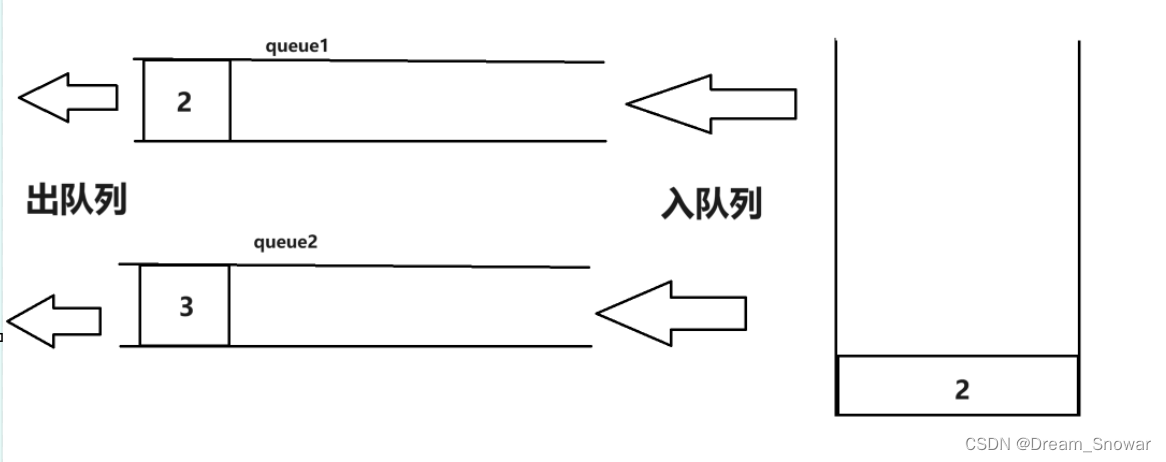
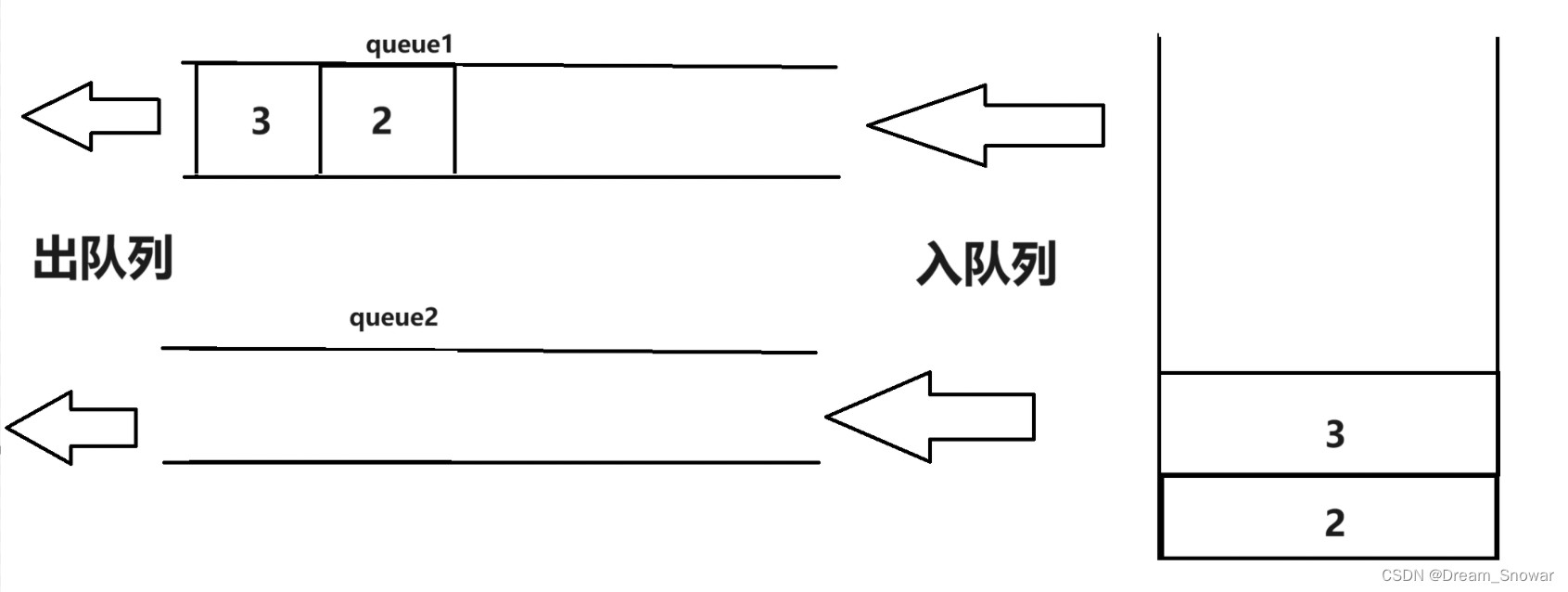
这样我们使用队列的pop就能达成和栈的pop一样的效果

接下来是代码演示：

#define LEN 20
typedef struct queue {
    int *data;
    int head;
    int rear;
    int size;
} Queue;

typedef struct {
    Queue *queue1, *queue2;
} MyStack;

Queue *initQueue(int k) {
    Queue *obj = (Queue *)malloc(sizeof(Queue));
    obj->data = (int *)malloc(k * sizeof(int));
    obj->head = -1;
    obj->rear = -1;
    obj->size = k;
    return obj;
}

void enQueue(Queue *obj, int e) {
    if (obj->head == -1) {
        obj->head = 0;
    }
    obj->rear = (obj->rear + 1) % obj->size;
    obj->data[obj->rear] = e;
}

int deQueue(Queue *obj) {
    int a = obj->data[obj->head];
    if (obj->head == obj->rear) {
        obj->rear = -1;
        obj->head = -1;
        return a;
    }
    obj->head = (obj->head + 1) % obj->size;
    return a;
}

int isEmpty(Queue *obj) {
    return obj->head == -1;
}

MyStack *myStackCreate() {
    MyStack *obj = (MyStack *)malloc(sizeof(MyStack));
    obj->queue1 = initQueue(LEN);
    obj->queue2 = initQueue(LEN);
    return obj;
}

void myStackPush(MyStack *obj, int x) {
    if (isEmpty(obj->queue1)) {
        enQueue(obj->queue2, x);
    } else {
        enQueue(obj->queue1, x);
    }
}

int myStackPop(MyStack *obj) {
    if (isEmpty(obj->queue1)) {
        while (obj->queue2->head != obj->queue2->rear) {
            enQueue(obj->queue1, deQueue(obj->queue2));
        }
        return deQueue(obj->queue2);
    }
    while (obj->queue1->head != obj->queue1->rear) {
        enQueue(obj->queue2, deQueue(obj->queue1));
    }
    return deQueue(obj->queue1);
}

int myStackTop(MyStack *obj) {
    if (isEmpty(obj->queue1)) {
        return obj->queue2->data[obj->queue2->rear];
    }
    return obj->queue1->data[obj->queue1->rear];
}

bool myStackEmpty(MyStack *obj) {
    if (obj->queue1->head == -1 && obj->queue2->head == -1) {
        return true;
    }
    return false;
}

void myStackFree(MyStack *obj) {
    free(obj->queue1->data);
    obj->queue1->data = NULL;
    free(obj->queue1);
    obj->queue1 = NULL;
    free(obj->queue2->data);
    obj->queue2->data = NULL;
    free(obj->queue2);
    obj->queue2 = NULL;
    free(obj);
    obj = NULL;
}

方法二、一个队列

这个思路整体和方法一差不多

使用一个队列时，为了满足栈的特性，即最后入栈的元素最先出栈，同样需要满足队列前端的元素是最后入栈的元素。入栈操作时，首先获得入栈前的元素个数 n，然后将元素入队到队列，再将队列中的前 n 个元素（即除了新入栈的元素之外的全部元素）依次出队并入队到队列，此时队列的前端的元素即为新入栈的元素，且队列的前端和后端分别对应栈顶和栈底。

先push一个2

再push一个3,记录星插入之前的所有数据

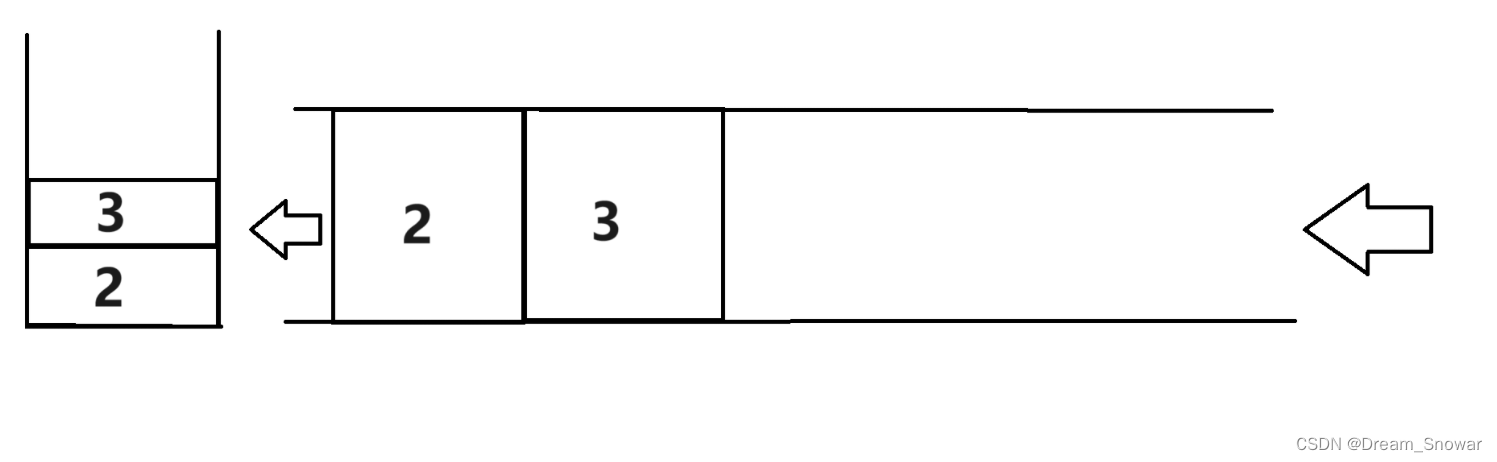
pop出之前的数据

把数据从队列后面入队列

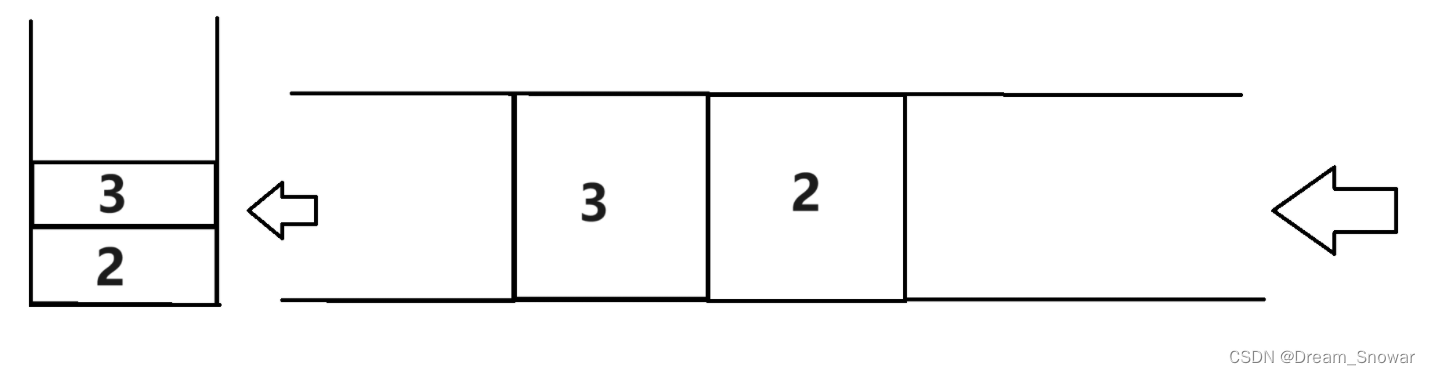
由于每次入栈操作都确保队列的前端元素为栈顶元素，因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可

简单来说就是把队列当成一个环用，每次都把除了队列末端的元素都出队然后依次加到原本末端元素的后端，这样原本最后的元素就被推到了队列最前端，实现了 Last In First Out

代码实现:

typedef struct tagListNode {
    struct tagListNode* next;
    int val;
} ListNode;

typedef struct {
    ListNode* top;
} MyStack;

MyStack* myStackCreate() {
    MyStack* stk = calloc(1, sizeof(MyStack));
    return stk;
}

void myStackPush(MyStack* obj, int x) {
    ListNode* node = malloc(sizeof(ListNode));
    node->val = x;
    node->next = obj->top;
    obj->top = node;
}

int myStackPop(MyStack* obj) {
    ListNode* node = obj->top;
    int val = node->val;
    obj->top = node->next;
    free(node);

    return val;
}

int myStackTop(MyStack* obj) {
    return obj->top->val;
}

bool myStackEmpty(MyStack* obj) {
    return (obj->top == NULL);
}

void myStackFree(MyStack* obj) {
    while (obj->top != NULL) {
        ListNode* node = obj->top;
        obj->top = obj->top->next;
        free(node);
    }
    free(obj);
}