算法

除了这里提到的算法思想和查找算法，算法还有别的类型：

排序算法： 对一组元素进行排序的算法。常见的排序算法包括冒泡排序、快速排序、归并排序等。

图算法： 解决图结构相关问题的算法，例如最短路径问题、最小生成树问题、图的遍历等。经典的图算法包括Dijkstra算法、Prim算法、深度优先搜索、广度优先搜索等。

字符串匹配算法： 解决字符串匹配问题的算法，例如暴力匹配、KMP算法、Boyer-Moore算法等。最长不重复子串: 使用滑动窗口来找到最长不重复子串。

排序和部分图在手撕那一篇，后续补齐：手撕java必备
 

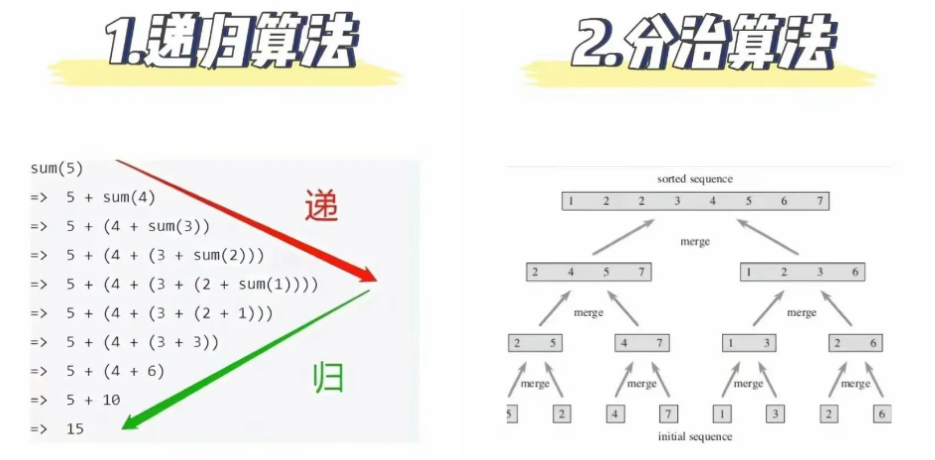
六大常用算法思想

告别动态规划，连刷40道动规算法题，我总结了动规的套路

常见查找算法

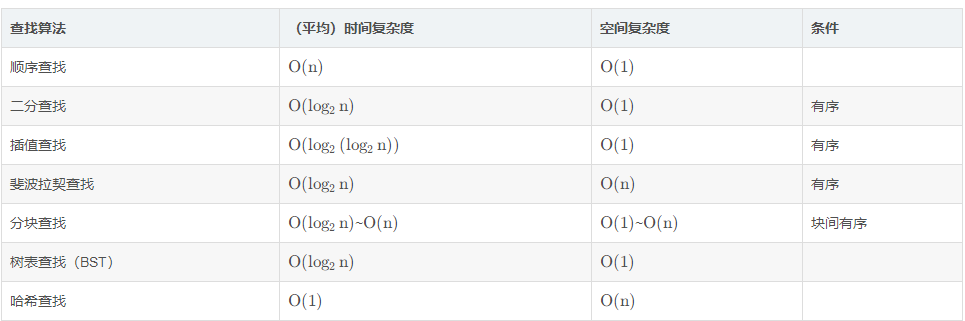
七大查找算法汇总

线性/顺序查找： 顺序遍历数据集，逐个比较元素，找到匹配项或达到数据集末尾。

二分查找： 仅适用于有序数据集。通过与中间元素的比较，将查找范围缩小一半，重复这个过程，直到找到匹配项或确定元素不在数据集中。

插值查找： 仅适用于有序数据集。根据元素的值在数据集中的相对位置进行估算，从而更快地找到匹配项。

斐波拉契查找：斐波那契搜索就是在二分查找的基础上根据斐波那契数列进行分割的。

分块查找（索引顺序查找）：分块查找又称索引顺序查找，是对顺序查找的一种改进方法。在此查找方法中，除了表本身外，还需要建立一个索引表。对表进行分块，分成几个子表，将子表中的索引保存至索引表，索引表按关键字有序，则分块有序。

树查找： 使用树结构进行查找，包括二叉搜索树（Binary Search Tree，BST）、平衡二叉搜索树（AVL树）、红黑树等。

哈希查找： 使用哈希函数将元素映射到一个地址，通过该地址直接访问元素。哈希表的实现可以使用数组或其他数据结构。

线性表

线性表是最常用且最简单的一种数据结构，它是n个数据元素的有限序列。

实现线性表的方式一般有两种，一种是使用数组存储线性表的元素，即用一组连续的存储单元依次存储线性表的数据元素。另一种是使用链表存储线性表的元素，即用一组任意的存储单元存储线性表的数据元素（存储单元可以是连续的，也可以是不连续的）。

数组

数组是一种大小固定的数据结构，对线性表的所有操作都可以通过数组来实现。虽然数组一旦创建之后，它的大小就无法改变了，但是当数组不能再存储线性表中的新元素时，我们可以创建一个新的大的数组来替换当前数组。这样就可以使用数组实现动态的数据结构。

代码1 创建一个更大的数组来替换当前数组

int[] oldArray = new int[10];
int[] newArray = new int[20];

for (int i = 0; i < oldArray.length; i++) {
    newArray[i] = oldArray[i];
}

// 也可以使用System.arraycopy方法来实现数组间的复制        
// System.arraycopy(oldArray, 0, newArray, 0, oldArray.length);

oldArray = newArray;

代码2 在数组位置index上添加元素e

//oldArray 表示当前存储元素的数组
//size 表示当前元素个数

public void add(int index, int e) {

    if (index > size || index < 0) {
        System.out.println("位置不合法...");
    }

    //如果数组已经满了 就扩容
    if (size >= oldArray.length) {
        // 扩容函数可参考代码1
    }

    for (int i = size - 1; i >= index; i--) {
        oldArray[i + 1] = oldArray[i];
    }

    //将数组elementData从位置index的所有元素往后移一位
    // System.arraycopy(oldArray, index, oldArray, index + 1,size - index);

    oldArray[index] = e;
    size++;
}

上面简单写出了数组实现线性表的两个典型函数，具体我们可以参考Java里面的ArrayList集合类的源码。数组实现的线性表优点在于可以通过下标来访问或者修改元素，比较高效，主要缺点在于插入和删除的花费开销较大，比如当在第一个位置前插入一个元素，那么首先要把所有的元素往后移动一个位置。为了提高在任意位置添加或者删除元素的效率，可以采用链式结构来实现线性表。

链表

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列节点组成，这些节点不必在内存中相连。每个节点由数据部分Data和链部分Next，Next指向下一个节点，这样当添加或者删除时，只需要改变相关节点的Next的指向，效率很高。

单链表

下面主要用代码来展示链表的一些基本操作，需要注意的是，这里主要是以单链表为例，暂时不考虑双链表和循环链表。

// 代码3 链表的节点
class Node<E> {
//泛型类 Node，其中 <E> 表示这是一个泛型类，E 是类型参数，表示这个节点可以存储任意类型的元素

    E item;
    Node<E> next;

    // 构造函数
    Node(E element) {
        this.item = element;
        this.next = null;
    }
}

// 代码4 定义好节点后，使用前一般是对头节点和尾节点进行初始化
// 头节点和尾节点都为空 链表为空
Node<E> head = null;
Node<E> tail = null;

// 代码5 空链表创建一个新节点
// 创建一个新的节点 并让head指向此节点
head = new Node("nodedata1");

// 让尾节点也指向此节点
tail = head;

// 代码6 链表追加一个节点
// 创建新节点 同时和最后一个节点连接起来
tail.next = new Node("node1data2");

// 尾节点指向新的节点
tail = tail.next;

// 代码7 顺序遍历链表
Node<String> current = head; // 从链表头开始，初始化一个指向当前节点的引用 current
while (current != null) {   // 循环直到链表尾部（null）
    System.out.println(current.item); // 打印当前节点的值
    current = current.next;  // 将当前节点引用移动到下一个节点
}

// 代码8 倒序遍历链表
static void printListRev(Node<String> head) {
    // 倒序遍历链表主要用了递归的思想
    if (head != null) {
        printListRev(head.next);
        System.out.println(head.item);
    }
}

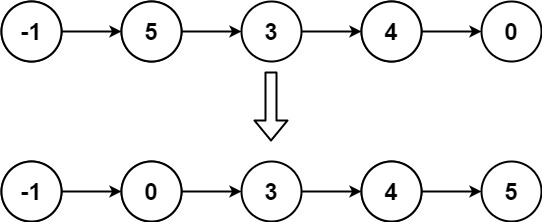
// 代码 单链表反转
// 单链表反转 主要是逐一改变两个节点间的链接关系来完成
static Node<String> revList(Node<String> head) {
    if (head == null) {
        return null;
    }

    Node<String> nodeResult = null;

    Node<String> nodePre = null;
    Node<String> current = head;

    while (current != null) {
        Node<String> nodeNext = current.next;

        if (nodeNext == null) {
            nodeResult = current;
        }

        current.next = nodePre;
        nodePre = current;
        current = nodeNext;
    }

    return nodeResult;
}

栈与队列

栈和队列也是比较常见的数据结构，它们是比较特殊的线性表，因为对于栈来说，访问、插入和删除元素只能在栈顶进行，对于队列来说，元素只能从队列尾插入，从队列头访问和删除。

栈

栈是限制插入和删除只能在一个位置上进行的表，该位置是表的末端，叫作栈顶，对栈的基本操作有push(进栈)和pop(出栈)，前者相当于插入，后者相当于删除最后一个元素。栈有时又叫作LIFO(Last In First Out)表，即后进先出。

因为栈也是一个表，所以任何实现表的方法都能实现栈。我们打开JDK中的类Stack的源码，可以看到它就是继承类Vector的。当然，Stack是Java2前的容器类，现在我们可以使用LinkedList来进行栈的所有操作。

队列

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

我们可以使用链表来实现队列，下面代码简单展示了利用LinkedList来实现队列类。

 //代码9 简单实现队列类
public class MyQueue<E> {
     private LinkedList<E> list = new LinkedList<>();

     // 入队
     public void enqueue(E e) {
         list.addLast(e);
     }

     // 出队
     public E dequeue() {
         return list.removeFirst();
     }
 }

普通的队列是一种先进先出的数据结构，而优先队列中，元素都被赋予优先级。当访问元素的时候，具有最高优先级的元素最先被删除。优先队列在生活中的应用还是比较多的，比如医院的急症室为病人赋予优先级，具有最高优先级的病人最先得到治疗。在Java集合框架中，类PriorityQueue就是优先队列的实现类，具体大家可以去阅读源码。

树与二叉树

树型结构是一类非常重要的非线性数据结构，其中以树和二叉树最为常用。在介绍二叉树之前，我们先简单了解一下树的相关内容。

树

树 是由n（n>=1）个有限节点组成一个具有层次关系的集合。它具有以下特点：每个节点有零个或多个子节点；没有父节点的节点称为 根 节点；每一个非根节点有且只有一个父节点 ；除了根节点外，每个子节点可以分为多个不相交的子树。

树和二叉树的区别

(1) 二叉树每个节点最多有2个子节点，树则无限制。 (2) 二叉树中节点的子树分为左子树和右子树，即使某节点只有一棵子树，也要指明该子树是左子树还是右子树，即二叉树是有序的。 (3) 树决不能为空，它至少有一个节点，而一棵二叉树可以是空的。

上面我们主要对二叉树的相关概念进行了介绍，下面我们将从二叉查找树开始，介绍二叉树的几种常见类型，同时将之前的理论部分用代码实现出来。

二叉树

二叉树是每个节点最多有两棵子树的树结构。通常子树被称作“左子树”和“右子树”。二叉树常被用于实现二叉查找树和二叉堆。

二叉树的每个结点至多只有2棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。

二叉树的第i层至多有2^(i-1)个结点；深度为k的二叉树至多有2^k-1个结点。

//代码10 二叉树的节点
 class TreeNode<E> {
     E element;
     TreeNode<E> left;
     TreeNode<E> right;  
  
    public TreeNode(E e) {
         element = e;
     }
 }

满二叉树

一棵深度为k，且有2^k-1个节点的二叉树称之为 满二叉树 。

完全二叉树

深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中，序号为1至n的节点对应时，称之为 完全二叉树 。

三种遍历：前、中、后序

在二叉树的一些应用中，常常要求在树中查找具有某种特征的节点，或者对树中全部节点进行某种处理，这就涉及到二叉树的遍历。二叉树主要是由3个基本单元组成，根节点、左子树和右子树。如果限定先左后右，那么根据这三个部分遍历的顺序不同，可以分为先序遍历、中序遍历和后续遍历三种。

(1) 先序遍历 若二叉树为空，则空操作，否则先访问根节点，再先序遍历左子树，最后先序遍历右子树。

(2) 中序遍历 若二叉树为空，则空操作，否则先中序遍历左子树，再访问根节点，最后中序遍历右子树。

(3) 后序遍历 若二叉树为空，则空操作，否则先后序遍历左子树访问根节点，再后序遍历右子树，最后访问根节点。

数学题：二叉树根据前序遍历和后序遍历，求解中序遍历

代码

二叉树遍历方法——前、中、后序遍历（java）

二叉树已知前序中序求后序(超简单)(java)

其它

二叉树--最近公共父节点

// 代码12 先序遍历
protected void preorder(TreeNode<E> root) {
    if (root == null)
        return;

    System.out.println(root.element + " ");
    preorder(root.left);
    preorder(root.right);
}

// 代码13 中序遍历
protected void inorder(TreeNode<E> root) {
    if (root == null)
        return;

    inorder(root.left);
    System.out.println(root.element + " ");
    inorder(root.right);
}

// 代码14 后序遍历
protected void postorder(TreeNode<E> root) {
    if (root == null)
        return;

    postorder(root.left);
    postorder(root.right);
    System.out.println(root.element + " ");
}

二叉查找树

二叉查找树（Binary Search Tree，BST）就是二叉排序树，也叫二叉搜索树。

二叉查找树或者是一棵空树，或者是具有下列性质的二叉树：

(1) 若左子树不空，则左子树上所有结点的值均小于它的根结点的值；

(2) 若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

(3) 左、右子树也分别为二叉排序树；

(4) 没有键值相等的结点。

性能分析：对于二叉查找树来说，当给定值相同但顺序不同时，所构建的二叉查找树形态是不同的。

典型的二叉查找树的构建过程

/**
 * 二叉查找树的简单实现
 * 
 * @author JackalTsc
 */
public class MyBinSearchTree<E extends Comparable<E>> {

    // 根
    private TreeNode<E> root;

    // 默认构造函数
    public MyBinSearchTree() {
    }

    // 二叉查找树的搜索
    public boolean search(E e) {
        TreeNode<E> current = root;

        while (current != null) {
            if (e.compareTo(current.element) < 0) {
                current = current.left;
            } else if (e.compareTo(current.element) > 0) {
                current = current.right;
            } else {
                return true;
            }
        }

        return false;
    }

    // 二叉查找树的插入
    public boolean insert(E e) {
        // 如果之前是空二叉树 插入的元素就作为根节点
        if (root == null) {
            root = createNewNode(e);
        } else {
            // 否则就从根节点开始遍历 直到找到合适的父节点
            TreeNode<E> parent = null;
            TreeNode<E> current = root;

            while (current != null) {
                if (e.compareTo(current.element) < 0) {
                    parent = current;
                    current = current.left;
                } else if (e.compareTo(current.element) > 0) {
                    parent = current;
                    current = current.right;
                } else {
                    return false;
                }
            }

            // 插入
            if (e.compareTo(parent.element) < 0) {
                parent.left = createNewNode(e);
            } else {
                parent.right = createNewNode(e);
            }
        }
        return true;
    }

    // 创建新的节点
    protected TreeNode<E> createNewNode(E e) {
        return new TreeNode(e);
    }
}

// 二叉树的节点
class TreeNode<E extends Comparable<E>> {
    E element;
    TreeNode<E> left;
    TreeNode<E> right;

    public TreeNode(E e) {
        element = e;
    }
}

含有n个节点的二叉查找树的平均查找长度和树的形态有关。

最坏情况下，当先后插入的关键字有序时，构成的二叉查找树蜕变为单支树，树的深度为n，其平均查找长度(n+1)/2(和顺序查找相同），最好的情况是二叉查找树的形态和折半查找的判定树相同，其平均查找长度和log2(n)成正比。

平均情况下，二叉查找树的平均查找长度和logn是等数量级的，所以为了获得更好的性能，通常在二叉查找树的构建过程需要进行“平衡化处理”，之后我们将介绍二叉平衡树和红黑树，这些均可以使查找树的高度为O(log(n))。

下面这些都是二叉查找树的不同变种，它们在解决BST的不足或性能优化方面有不同的设计：

二叉平衡树

为了解决二叉查找树不平衡的问题，引入了平衡树的概念。平衡树确保左右子树的高度差不超过某个限定值，以保持树的平衡。

AVL树

AVL树就是一种二叉平衡树的具体实现，通过在每个节点上维护平衡因子（左子树高度减去右子树高度），保持树的平衡。

平衡二叉树（AVL树）是一种特殊的二叉搜索树，它的左右子树的高度差不超过1。AVL树的平衡性质保证了在最坏情况下，树的高度为O(log n)，从而实现了快速的查找、插入和删除操作。

AVL树的平衡是通过旋转操作来维持的，包括左旋、右旋、左右旋和右左旋。这些旋转操作保持了树的平衡性质，但是在进行插入和删除等操作时，可能需要执行多次旋转。

不同形态平衡二叉树的ASL不同：

AVL树的平衡性质决定了在任何给定时刻，树中任意节点的左右子树高度差最多为1。因此，AVL树的平均搜索长度（ASL）可以保持较小的值，通常为O(log n)。

JAVA实现平衡二叉树（AVL）

class AVLNode {
    int key, height;
    AVLNode left, right;

    public AVLNode(int key) {
        this.key = key;
        this.height = 1;
    }
}

class AVLTree {
    AVLNode root;

    // 获取树的高度
    int height(AVLNode node) {
        if (node == null) return 0;
        return node.height;
    }

    // 获取最大值
    int max(int a, int b) {
        return (a > b) ? a : b;
    }

    // 计算节点的平衡因子
    int getBalance(AVLNode node) {
        if (node == null) return 0;
        return height(node.left) - height(node.right);
    }

    // 右旋
    AVLNode rightRotate(AVLNode y) {
        AVLNode x = y.left;
        AVLNode T2 = x.right;

        x.right = y;
        y.left = T2;

        y.height = max(height(y.left), height(y.right)) + 1;
        x.height = max(height(x.left), height(x.right)) + 1;

        return x;
    }

    // 左旋
    AVLNode leftRotate(AVLNode x) {
        AVLNode y = x.right;
        AVLNode T2 = y.left;

        y.left = x;
        x.right = T2;

        x.height = max(height(x.left), height(x.right)) + 1;
        y.height = max(height(y.left), height(y.right)) + 1;

        return y;
    }

    // 插入节点
    AVLNode insert(AVLNode node, int key) {
        if (node == null) return new AVLNode(key);

        if (key < node.key)
            node.left = insert(node.left, key);
        else if (key > node.key)
            node.right = insert(node.right, key);
        else // 重复的键不被允许
            return node;

        // 更新节点的高度
        node.height = 1 + max(height(node.left), height(node.right));

        // 获取平衡因子
        int balance = getBalance(node);

        // 左旋
        if (balance > 1 && key < node.left.key)
            return rightRotate(node);

        // 右旋
        if (balance < -1 && key > node.right.key)
            return leftRotate(node);

        // 左右旋
        if (balance > 1 && key > node.left.key) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }

        // 右左旋
        if (balance < -1 && key < node.right.key) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }

        return node;
    }

    // 中序遍历以打印树
    void inOrder(AVLNode node) {
        if (node != null) {
            inOrder(node.left);
            System.out.print(node.key + " ");
            inOrder(node.right);
        }
    }
}

public class AVLTreeExample {
    public static void main(String[] args) {
        AVLTree avlTree = new AVLTree();

        // 插入节点
        avlTree.root = avlTree.insert(avlTree.root, 10);
        avlTree.root = avlTree.insert(avlTree.root, 20);
        avlTree.root = avlTree.insert(avlTree.root, 30);

        // 中序遍历以打印树
        avlTree.inOrder(avlTree.root);
    }
}

红黑树

红黑树是另一种常用的自平衡二叉树，它对于插入和删除操作的平均性能略优于AVL树，但在查找操作上稍逊于AVL树。

平衡二叉树之红黑树java实现

索引树（除红黑树）

索引树（Index Tree）是一种数据结构，用于在数据库和文件系统等应用中加速对数据的检索操作。索引树通常以树的形式组织，其中包括树根、内部节点和叶子节点。常见的索引树结构包括B树（B-tree）、B+树（B-plus-tree）、B树（B-star tree）、红黑树。

B树、B+树、B*树

B-树、B树和B+树

Java数据结构和算法---多路查找树(B树、B+树和B*树)