机器学习评价指标（分类、目标检测）

https://zhuanlan.zhihu.com/p/364253497
https://zhuanlan.zhihu.com/p/46714763
https://blog.csdn.net/u013250861/article/details/123029585

1.1 混淆矩阵

在介绍评价指标之前，我们首先要介绍一下混淆矩阵（confusion matrix）。
混淆矩阵本身是对于预测结果的一个粗略评价，可以让我们对预测结果和原始数据有一个宏观的了解。同时我们也会在计算后面的评价指标时用到混淆矩阵中的数。

混淆矩阵里面有四个格子，包含了我们在进行一个二分类预测的时候，预测结果所有可能出现的情况。也就是说，对于任何一个样本进行预测以后，预测结果一定属于这四个格子的其中一个：
True Positive（TP）表示实际上这个样本为Positive，模型也把这个样本预测为Positive的情况。这是我们预测正确的部分。
True Negative（TN）表示实际上这个样本为Negative，模型也把这个样本预测为Negative的情况。这是我们预测正确的部分。
False Positive（FP）表示实际上这个样本为Negative，但是模型预测为了Positive的情况。这是预测错误的部分，也是统计学上的第一类错误。
False Negative（FN）表示实际上这个样本为Positive，但是模型预测为了Negative的情况。这是预测错误的部分，也是统计学上的第二类错误。

1.2 准确率ACC

Accuracy，中文为准确率，指的是预测正确的样本数除于样本数总数。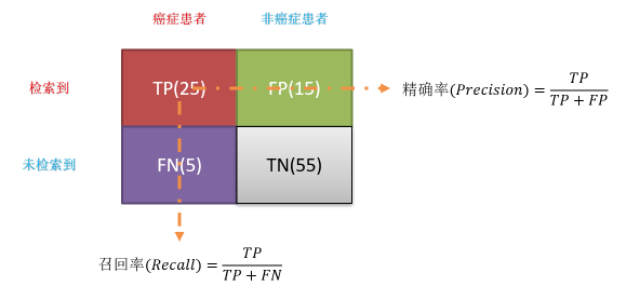

计算公式为：

通常我们没有负样本：
acc = TP / (TP+FP）

优点	缺点
- 准确率的优点是比较简单直观。 - 通常我们在如下情况的时候使用Accuracy： - 数据集是平衡的； - 我们要向对于机器学习与数据科学不熟悉的人解释我们的模型； - 每一类label对我们来说是一样重要的。因为Accuracy同时考虑了Positive samples和Negative samples。	不适用于不平衡数据

例：我们要预测当天是否会发生地震。
由于在某一天内不会发生地震的概率可能性接近99.99%，模型会倾向于无脑地把所有的日子全部预测为不会发生地震，这样它的accuracy将会高达99.99%，只有在那0.01%的、会发生地震的日子是预测错的。
这样的模型虽然accuracy非常高，但是没有任何意义。毕竟我们要的就是在这0.01%的日子把地震预测出来，你全部预测成“没有地震”了要你还有什么用。
在这种情况下，accuracy显然是一个非常差的指标，它无法衡量一个模型的真实预测能力。

1.3 精确率Precision

Precision，中文为精确率或者精度，指的是在我们预测为True的样本里面，有多少确实为True的。在信息检索领域，precision也被称为“查准率”。
其公式为：

如果我们要求precision高，那么我们是在“求精”，也就是我们不指望着把所有的positive samples都找出来，但是我们希望在我们挑出来的人里面，各个都要是“精英”；“被选中的这批人”一定要干净、纯粹，那些“鱼目混珠”的negative sample越少越好。哪怕是有些“潜力股”被我们放走了也在所不惜。
我们可以把高precision的模型看做是一个谨小慎微、小心翼翼的“检察官”，他对“质”的要求很高，哪怕我抓到的人很少也没关系，但只要是我抓出来的人，就一定是犯过事的。他绝不冤枉一个好人。
Precision的分母是我们预测的结果。也就是，我们三下五除二对所有的样本进行预测，交了一份答卷以后，看看我们预测为True的样本里面真的是True的比例有多大，所以叫做precision精确率。简记为“Precision对应着预测”。

（二）什么情况下我们要求Precision要高？
当“把一个实际是False的样本错标为True”的成本很高，但是“把一个实际是True的样本错标为False”成本很低的时候。
也可以简记为：“冤假错案”成本高，“漏网之鱼”成本低。
这里我们举一个例子。
例：判断一封邮件是否是垃圾邮件，是则为True，否则为False。
“冤假错案”成本高：我们知道，邮件沟通相比于微信、短信、电话，一般是用于较为正式的场合，传达了重要的、高价值的信息。这时候，如果我们把一封正常（False）的邮件标记为垃圾邮件（True），这个错误的代价对我们来说太高了，说不定人家几百万的合同、学校的录取通知书、某一产品的注册确认信息就被你标记为垃圾邮件了。
“漏网之鱼”成本低：如果有一些垃圾邮件没有被标记出来，这个的成本是非常低的，大不了就是用户看见了垃圾邮件，多花几秒钟瞟一眼，然后退出来。也就是几秒钟的时间成本。
这时候，我们就要求标记“垃圾邮件”的过程要“求精不求多”，必须一定是“垃圾邮件”才能被我们标记为True，哪怕代价是放过几只漏网之鱼也没关系。因此，在这个案例中，我们要求precision要高。

1.4 召回率recall

召回率（Recall）又叫查全率，它是针对原样本而言的，它的含义是在实际为正的样本中被预测为正样本的概率，其公式如下：
精准率=TP/(TP+FN)

**召回率的应用场景：**比如拿网贷违约率为例，相对好用户，我们更关心坏用户，不能错放过任何一个坏用户。因为如果我们过多的将坏用户当成好用户，这样后续可能发生的违约金额会远超过好用户偿还的借贷利息金额，造成严重偿失。召回率越高，代表实际坏用户被预测出来的概率越高，它的含义类似：宁可错杀一千，绝不放过一个。

1.5 精准率和召回率的关系，F1分数

通过上面的公式，我们发现：精准率和召回率的分子是相同，都是TP，但分母是不同的，一个是（TP+FP），一个是（TP+FN）。两者的关系可以用一个P-R图来展示：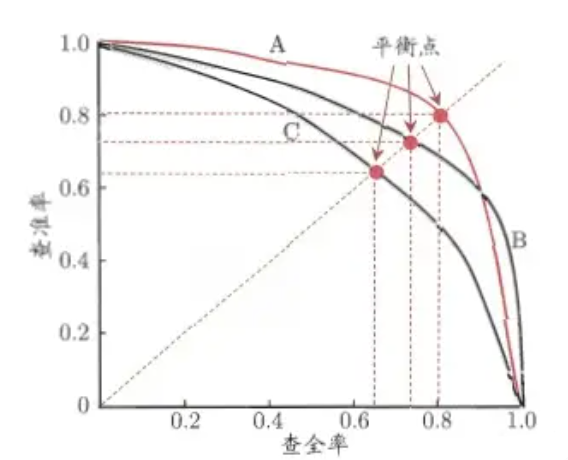

** 如何理解P-R（查准率-查全率）这条曲线？**
有的朋友疑惑：这条曲线是根据什么变化的？为什么是这个形状的曲线？其实这要从排序型模型说起。拿逻辑回归举例，逻辑回归的输出是一个0到1之间的概率数字，因此，如果我们想要根据这个概率判断用户好坏的话，我们就必须定义一个阈值。通常来讲，逻辑回归的概率越大说明越接近1，也就可以说他是坏用户的可能性更大。比如，我们定义了阈值为0.5，即概率小于0.5的我们都认为是好用户，而大于0.5都认为是坏用户。因此，对于阈值为0.5的情况下，我们可以得到相应的一对查准率和查全率。
但问题是：这个阈值是我们随便定义的，我们并不知道这个阈值是否符合我们的要求。因此，为了找到一个最合适的阈值满足我们的要求，我们就必须遍历0到1之间所有的阈值，而每个阈值下都对应着一对查准率和查全率，从而我们就得到了这条曲线。
有的朋友又问了：**如何找到最好的阈值点呢？**首先，需要说明的是我们对于这两个指标的要求：**我们希望查准率和查全率同时都非常高。**但实际上这两个指标是一对矛盾体，无法做到双高。图中明显看到，如果其中一个非常高，另一个肯定会非常低。选取合适的阈值点要根据实际需求，比如我们想要高的查全率，那么我们就会牺牲一些查准率，在保证查全率最高的情况下，查准率也不那么低。

F1分数
但通常，如果想要找到二者之间的一个平衡点，我们就需要一个新的指标：F1分数。F1分数同时考虑了查准率和查全率，让二者同时达到最高，取一个平衡。F1分数的公式为 = **2查准率查全率 / (查准率 + 查全率)。**我们在图中看到的平衡点就是F1分数得来的结果。

1.6 ROC/AUC的概念

1. 灵敏度，特异度，真正率，假正率
在正式介绍ROC/AUC之前，我们还要再介绍两个指标，**这两个指标的选择也正是ROC和AUC可以无视样本不平衡的原因。**这两个指标分别是：灵敏度和（1-特异度），也叫做真正率（TPR）和假正率（FPR）。
灵敏度（Sensitivity） = TP/(TP+FN)
特异度（Specificity） = TN/(FP+TN)

其实我们可以发现灵敏度和召回率是一模一样的，只是名字换了而已。
由于我们比较关心正样本，所以需要查看有多少负样本被错误地预测为正样本，所以使用（1-特异度），而不是特异度。

真正率（TPR） = 灵敏度 = TP/(TP+FN)
假正率（FPR） = 1- 特异度 = FP/(FP+TN)
下面是真正率和假正率的示意，我们发现**TPR和FPR分别是基于实际表现1和0出发的，也就是说它们分别在实际的正样本和负样本中来观察相关概率问题。**正因为如此，所以无论样本是否平衡，都不会被影响。还是拿之前的例子，总样本中，90%是正样本，10%是负样本。我们知道用准确率是有水分的，但是用TPR和FPR不一样。
这里，TPR只关注90%正样本中有多少是被真正覆盖的，而与那10%毫无关系，同理，FPR只关注10%负样本中有多少是被错误覆盖的，也与那90%毫无关系，所以可以看出：如果我们从实际表现的各个结果角度出发，就可以避免样本不平衡的问题了，这也是为什么选用TPR和FPR作为ROC/AUC的指标的原因。

或者我们也可以从另一个角度考虑：条件概率。我们假设X为预测值，Y为真实值。那么就可以将这些指标按条件概率表示：
精准率 = P（Y=1 | X=1）
召回率 = 灵敏度 = P（X=1 | Y=1）
特异度 = P（X=0 | Y=0）