数据结构小记【Python/C++版】—

数据结构小记【Python/C++版】——B树篇

news2024/9/28 7:26:00

一，基础概念

B树也是一种自平衡搜索树，常用于数据库中索引的实现。

B树和AVL树的区别在于：

B树是一种多路平衡查找树，B树的节点可以有两个以上的子节点(AVL树是二叉树，最多只能有两个子节点)。

B树的每个节点可以存储一个以上的数据域(在之前介绍过的树结构中，一个节点只有一个数据域)。由于B树的节点可以存放多条数据，因此B树特别适合应用在块存储的开发场景。

B树和AVL树的相同点在于：

B树的节点分布也是按照左小右大排列，子节点与节点的大小比较结果决定了子节点的位置。

每个节点中，左子树的数据比当前节点都小，右子树的数据比当前节点都大。

关于B树的阶：

M阶B树表示该树每个节点最多有M个子树。若B树中一个节点的子节点数目的最大值为4，则该树为4阶。

M阶B树可以定义为M路搜索树：

节点的最多子节点数为M。

节点的最大数据量为M-1。

所有非叶子节点(根节点除外)应该至少有M/2个子节点。

所有节点(根节点除外)应该至少有M/2-1条数据。

B树的阶数可以帮助我们确定节点在B树中可以容纳的子节点数。如果B树的阶数为3，则子节点的最小数量为2，最大数量为3，节点最多可以存放2个数据。类似地，如果B树的阶数为4，则子节点的最小和最大数量将分别为2和4，节点最多可以存放3个数据。

B树的基本结构：

B树的结构特点：

所有叶子节点都出现在同一水平高度。

B树是一棵扁平树，层数很小，B树的节点不再只存储一条数据。

B树节点内的所有数据必须按键值升序排列。

B树的设计原则就是，将尽可能多的数据放入B树的每个节点中，从而使B树的层数保持在最小值。由于不用遍历很多层节点，与其他平衡树相比，B树的访问速度更快。

二，B树的基本操作

搜索节点：

节点在B树中的搜索步骤与BST树中的类似。

插入节点：

如果树为空，则创建一个新节点并将其作为根节点插入到树中。

如果树不为空，插入节点包含两个操作：

1.搜索合适的位置以插入节点

按照升序插入节点。

2.当节点的数据量过大时拆分节点

插入新节点以后，节点中数据的数量超过了限制(节点的最大数据量为M-1)，则按中位数拆分。将中间节点推往上一层，使左边节点成为左子节点，右边节点成为右子节点。

图示样例：

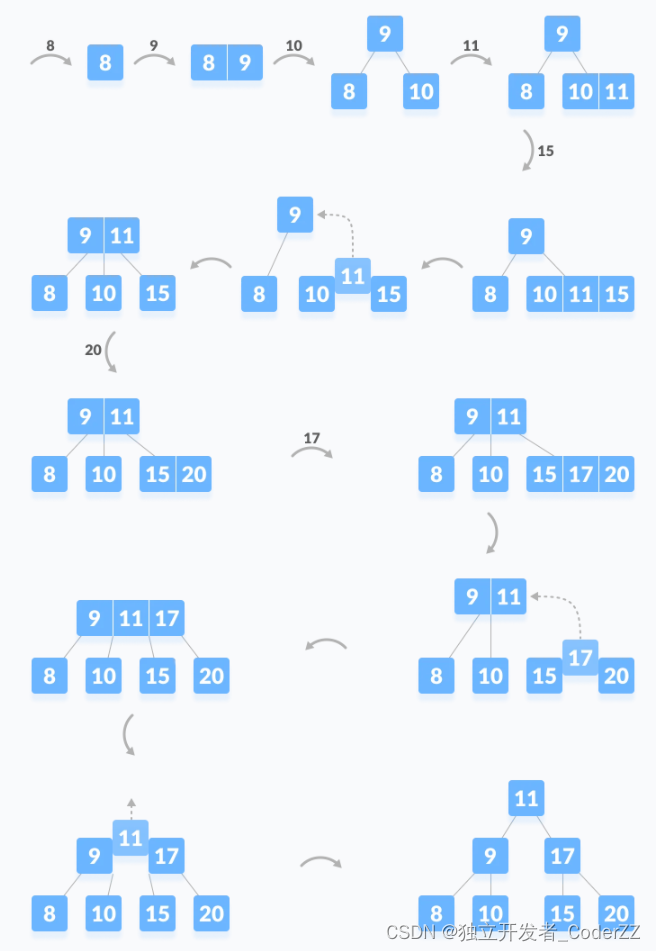
三，完整代码实现

C++实现：

#include <iostream>
using namespace std;
class Node {
    int* keys;
    int t;
    Node** C;
    int n;
    bool leaf;
public:
    Node(int _t, bool _leaf);
    void insertNonFull(int k);
    void splitChild(int i, Node* y);
    void traverse();
    friend class BTree;
};
class BTree {
    Node* root;
    int t;
public:
    BTree(int _t) {
        root = NULL;
        t = _t;
    }
    void traverse() {
        if (root != NULL)
            root->traverse();
    }
    void insert(int k);
};
Node::Node(int t1, bool leaf1) {
    t = t1;
    leaf = leaf1;
    keys = new int[2 * t - 1];
    C = new Node * [2 * t];
    n = 0;
}
//遍历节点
void Node::traverse() {
    int i;
    for (i = 0; i < n; i++) {
        if (leaf == false)
            C[i]->traverse();
        cout << " " << keys[i];
    }
    if (leaf == false)
        C[i]->traverse();
}
void BTree::insert(int k) {
    if (root == NULL) {
        root = new Node(t, true);
        root->keys[0] = k;
        root->n = 1;
    }
    else {
        if (root->n == 2 * t - 1) {
            Node* s = new Node(t, false);
            s->C[0] = root;
            s->splitChild(0, root);
            int i = 0;
            if (s->keys[0] < k)
                i++;
            s->C[i]->insertNonFull(k);
            root = s;
        }
        else
            root->insertNonFull(k);
    }
}
void Node::insertNonFull(int k) {
    int i = n - 1;
    if (leaf == true) {
        while (i >= 0 && keys[i] > k) {
            keys[i + 1] = keys[i];
            i--;
        }
        keys[i + 1] = k;
        n = n + 1;
    }
    else {
        while (i >= 0 && keys[i] > k)
            i--;
        if (C[i + 1]->n == 2 * t - 1) {
            splitChild(i + 1, C[i + 1]);
            if (keys[i + 1] < k)
                i++;
        }
        C[i + 1]->insertNonFull(k);
    }
}
//拆分节点
void Node::splitChild(int i, Node* y) {
    Node* z = new Node(y->t, y->leaf);
    z->n = t - 1;
    for (int j = 0; j < t - 1; j++)
        z->keys[j] = y->keys[j + t];
    if (y->leaf == false) {
        for (int j = 0; j < t; j++)
            z->C[j] = y->C[j + t];
    }
    y->n = t - 1;
    for (int j = n; j >= i + 1; j--)
        C[j + 1] = C[j];
    C[i + 1] = z;
    for (int j = n - 1; j >= i; j--)
        keys[j + 1] = keys[j];
    keys[i] = y->keys[t - 1];
    n = n + 1;
}
int main() {
    BTree t(3);
    t.insert(8);
    t.insert(9);
    t.insert(10);
    t.insert(11);
    t.insert(15);
    t.insert(20);
    t.insert(17);
    cout << "The B-tree is: ";
    t.traverse();
}

运行结果：

The B-tree is:  8 9 10 11 15 17 20

Python实现：

class BTreeNode:
    def __init__(self, leaf=False):
        self.leaf = leaf
        self.keys = []
        self.child = []

class BTree:
    def __init__(self, t):
        self.root = BTreeNode(True)
        self.t = t

    def insert(self, k):
        root = self.root
        if len(root.keys) == (2 * self.t) - 1:
            temp = BTreeNode()
            self.root = temp
            temp.child.insert(0, root)
            self.split_child(temp, 0)
            self.insert_non_full(temp, k)
        else:
            self.insert_non_full(root, k)

    def insert_non_full(self, x, k):
        i = len(x.keys) - 1
        if x.leaf:
            x.keys.append((None, None))
            while i >= 0 and k[0] < x.keys[i][0]:
                x.keys[i + 1] = x.keys[i]
                i -= 1
            x.keys[i + 1] = k
        else:
            while i >= 0 and k[0] < x.keys[i][0]:
                i -= 1
            i += 1
            if len(x.child[i].keys) == (2 * self.t) - 1:
                self.split_child(x, i)
                if k[0] > x.keys[i][0]:
                    i += 1
            self.insert_non_full(x.child[i], k)

    def split_child(self, x, i):
        t = self.t
        y = x.child[i]
        z = BTreeNode(y.leaf)
        x.child.insert(i + 1, z)
        x.keys.insert(i, y.keys[t - 1])
        z.keys = y.keys[t: (2 * t) - 1]
        y.keys = y.keys[0: t - 1]
        if not y.leaf:
            z.child = y.child[t: 2 * t]
            y.child = y.child[0: t - 1]

    def print_tree(self, x, l=0):
        print("Level ", l, " ", len(x.keys), end=":")
        for i in x.keys:
            print(i, end=" ")
        print()
        l += 1
        if len(x.child) > 0:
            for i in x.child:
                self.print_tree(i, l)

def main():
    B = BTree(3)
    for i in range(10):
        B.insert((i, 2 * i))
    B.print_tree(B.root)

if __name__ == '__main__':
    main()