资源限制
内存限制:256.0MB C/C++时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s
问题描述
在那个过河卒逃过了马的控制以超级超级多的走法走到了终点之后,这匹马表示它不开心了……
于是,终于有一天,它也过河了!
由于过河马积累了许多的怨念,所以这次它过了河之后,再也没有什么东西可以限制它,它可以自由自在的在棋盘上驰骋。一开始,它是在一个n行m列棋盘的左下角(1,1)的位置,它想要走到终点右上角(n,m)的位置。而众所周知,马是要走日子格的。可是这匹马在积累了这么多怨念之后,它再也不想走回头路——也就是说,它只会朝向上的方向跳,不会朝向下的方向跳。
那么,这匹马它也想知道,它想从起点跳到终点,一共有多少种走法呢?
输入格式
第一行两个数n,m,表示一个n行m列的棋盘,马最初是在左下角(1,1)的位置,终点在右上角(n,m)的位置。
输出格式
输出有一行,一个数表示走法数。由于答案可能很大,所以输出答案除以1000000007所得的余数即可。
样例输入
4 4
样例输出
2
数据规模和约定
n<=100,m<=100
#include<iostream>
using namespace std;
#define A 1000000007
const int N=105;
int dp[N][N];//dp[i][j]:表示从(1,1)到(i,j)一共有dp[i][j]种方法
int main(){
int n,m;
scanf("%d%d",&n,&m);
//初始化
dp[3][2]=1,dp[2][3]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(i-1>=1&&j-2>=1){//从(i-1,j-2)跳到(i,j)
dp[i][j]=dp[i][j]+dp[i-1][j-2];
dp[i][j]%=A;
}
if(i-2>=1&&j-1>=1){//从(i-2,j-1)跳到(i,j)
dp[i][j]=dp[i][j]+dp[i-2][j-1];
dp[i][j]%=A;
}
if(i-2>=1&&j+1<=m){//从(i-2,j+1)跳到(i,j)
dp[i][j]=dp[i][j]+dp[i-2][j+1];
dp[i][j]%=A;
}
if(i-1>=1&&j+2<=m){//从(i-1,j+2)跳到(i,j)
dp[i][j]=dp[i][j]+dp[i-1][j+2];
dp[i][j]%=A;
}
}
}
printf("%d\n",dp[n][m]);
return 0;
}  思路:dp。dp[i][j]:表示从(1,1)到(i,j)一共有dp[i][j]种方法,所以答案为dp[n][m]。走一次跳到(i,j),有四种情况,总共次数就是把这4种加起来。注意,不能用dfs,因为n<=100,dfs的时间复杂度是指数级的。
思路:dp。dp[i][j]:表示从(1,1)到(i,j)一共有dp[i][j]种方法,所以答案为dp[n][m]。走一次跳到(i,j),有四种情况,总共次数就是把这4种加起来。注意,不能用dfs,因为n<=100,dfs的时间复杂度是指数级的。
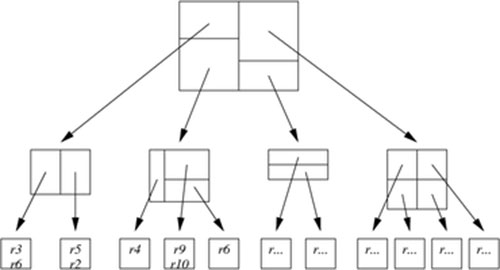
从(1,1)到(n,m),只能向下走:(和题目是一样的意思,只不过反了一下)
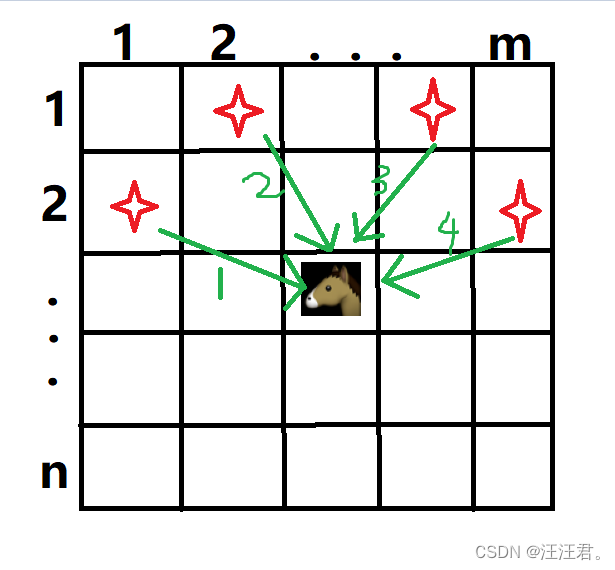
要到达![]() ,有4种方法,将其相加即为总数。dp[i][j]=dp[i-1][j-2]+dp[i-2][j-1]+dp[i-2][j+1]+dp[i-1][j+2],分别对应着走法1、2 、3、4,只不过还要判断一下有没有越界。
,有4种方法,将其相加即为总数。dp[i][j]=dp[i-1][j-2]+dp[i-2][j-1]+dp[i-2][j+1]+dp[i-1][j+2],分别对应着走法1、2 、3、4,只不过还要判断一下有没有越界。









![基于51单片机的定时器时钟设计[proteus仿真]](https://img-blog.csdnimg.cn/direct/60d7f9d236c7413ab0e32ce0e2eddae8.png)