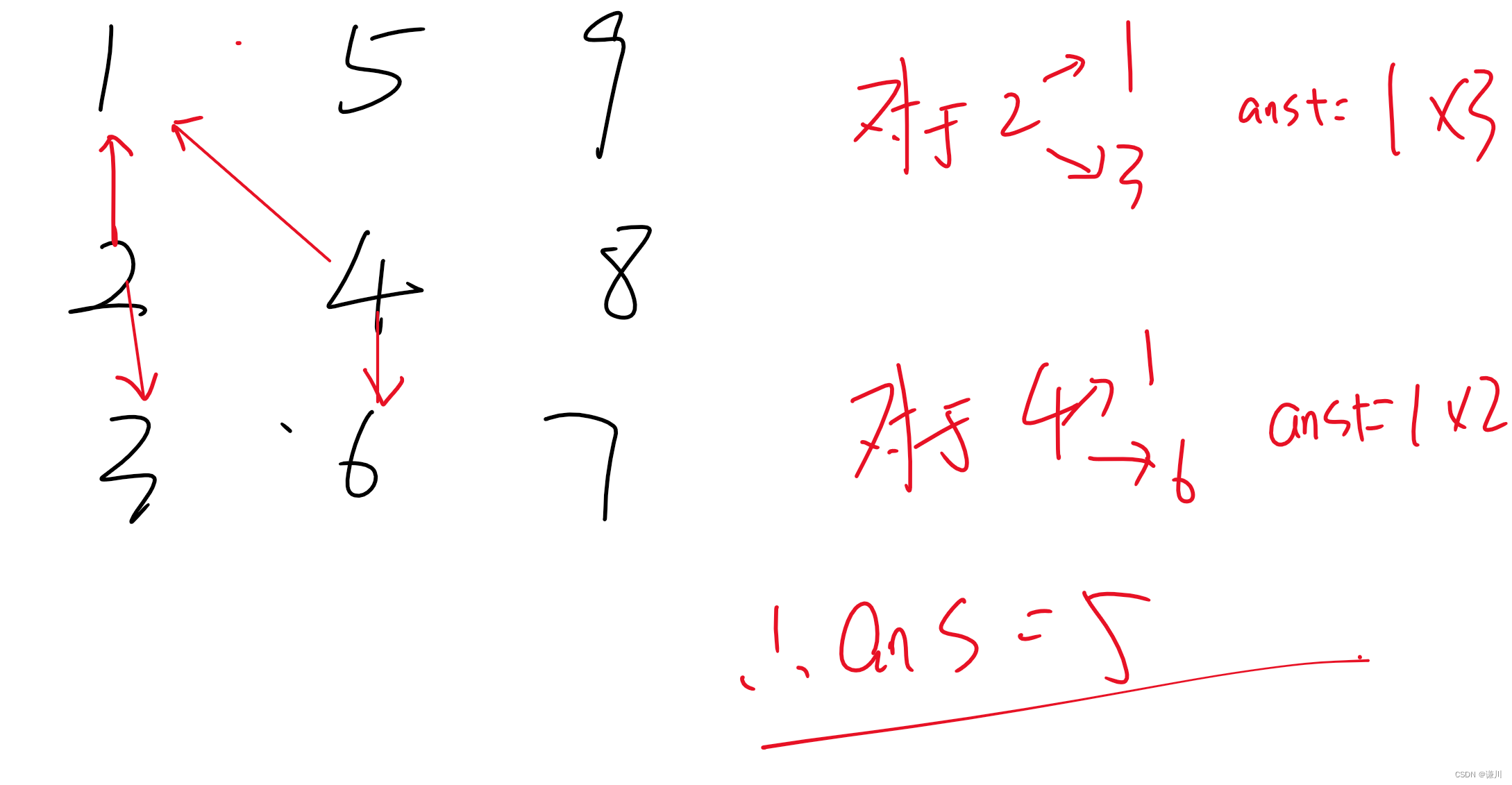【软考】图的遍历

- - - 1. 概念
    - 2. 深度优先搜索
    - - 2.1 说明
      - 2.2 步骤
    - 3. 深度优先搜索例子
    - - 3.1 无向图
      - 3.2 代码示例
      - 3.3 结果示例
      - 3.4 过程
    - 4. 广度优先搜索
    - - 4.1 说明
      - 4.2 步骤
    - 5. 广度优先搜索例子
    - - 5.1 无向图
      - 5.2 代码示例
      - 5.3 结果示例
      - 5.4 过程
      - 5.5 例题
      - 5.5.1 题目1

1. 概念

1.图的遍历是指从某个顶点出发，沿着某条搜索路径对图中的所有顶点进行访问且只访问一次的过程
2.图的遍历算法是求解图的连通性问题、拓扑排序及求关键路径等算法的基础
3.图的遍历比树的遍历复杂
4.图的任一个结点都可能与其余顶点相邻接，所以在访问了某个顶点之后，可能沿着某路径又回到该结点上，为了避免对顶点进行重复访问，在图的遍历过程中必须记下每个已访问过的顶点
5.深度优先搜索和广度优先搜索是两种遍历图的基本方法

2. 深度优先搜索

2.1 说明

1.Depth First Search, DFS
2.类似于树的先根比遍历，在第一次经过一个顶点时就进行访问访问操作
3.深度优先遍历图的过程实质上是对某个顶点查找其邻接点的过程，其耗费的时间取决于所采用的存储结构
4.当图用邻接矩阵表示时，查找所有顶点的邻接点所需时间为 O(n)。
5.若以邻接表作为图的存储结构，则需要 O(e)的时间复杂度查找所有顶点的邻接点。因此，当以邻接表作为存储结构时，深度优先搜索遍历图的时间复杂度为 O(n+e)。

2.2 步骤

1.设置搜索指针p，使p指向顶点v
2.访问p所指顶点，并使p指向与其相邻接的且尚未被访问过的顶点
3.若p所指顶点存在，则重复步骤2，否则执行步骤4
4.沿着刚才访问的次序和方向回溯到一个尚有邻接顶点且未被访问过的顶点，并使p指向这个未被访问的顶点，然后重复步骤2，直到所有的顶点均被访问为止
5.该算法的特点是尽可能先对纵深方向搜索，因此可以得到其递归遍历算法
6.

3. 深度优先搜索例子

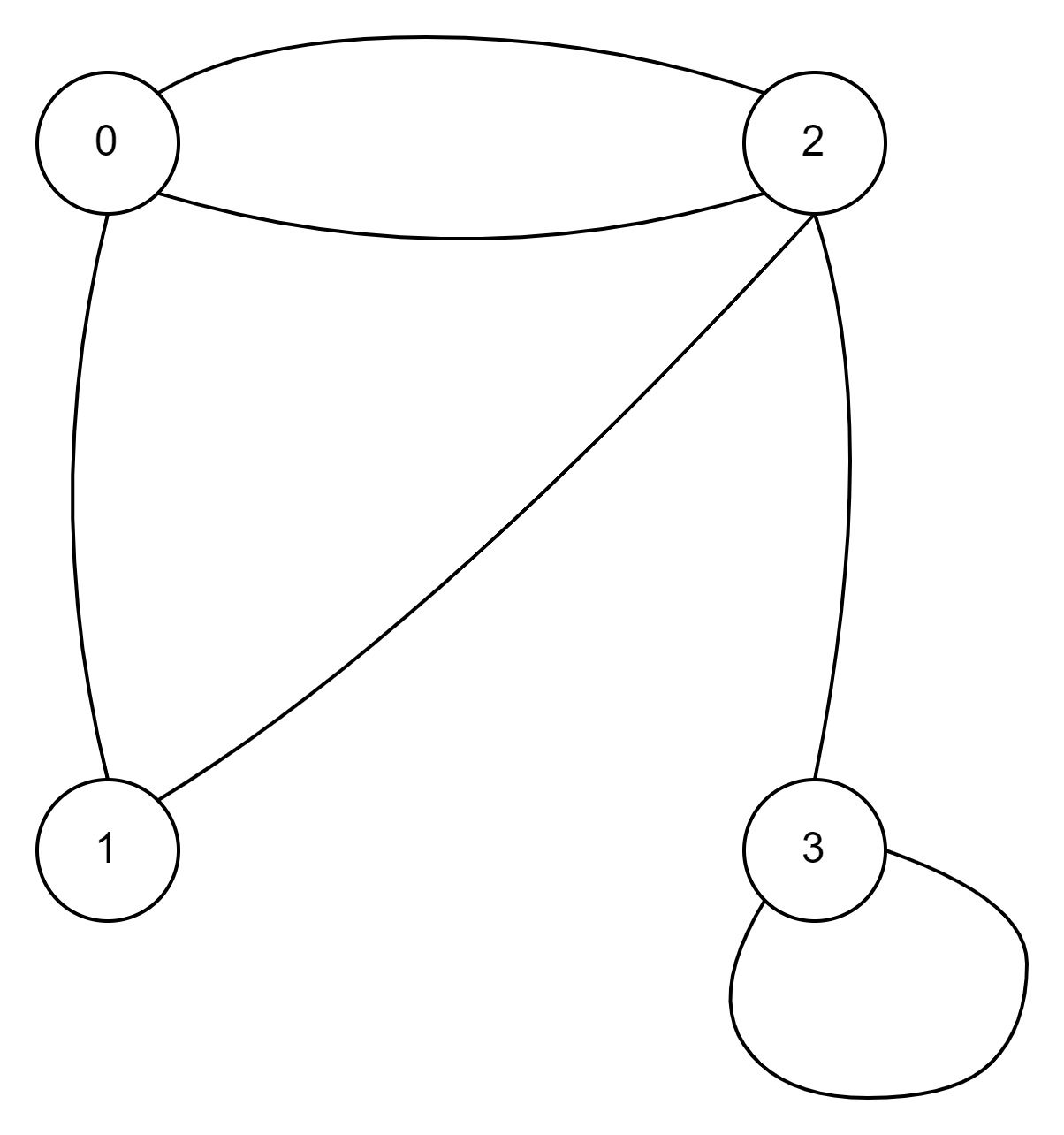
3.1 无向图

3.2 代码示例

package com.learning.algorithm.search.graph;

import java.util.*;

public class Graph {
    // 顶点的数量
    private int number;
    // 邻接列表
    private LinkedList<Integer>[] adjacency;

    public Graph(int number) {
        this.number = number;
        adjacency = new LinkedList[number];
        for (int i = 0; i< number; ++i) {
            adjacency[i] = new LinkedList();
        }
    }

    // 向图中添加边
    public void addEdge(int v, int w) {
        adjacency[v].add(w);
    }

    // 从v可达顶点的深度优先搜索
    public void depthFirstSearch(int v, boolean visited[]) {
        // 将当前节点标记为已访问并打印
        visited[v] = true;
        System.out.print(v+" ");

        // 对与此顶点相邻的所有顶点重复搜索
        Iterator<Integer> i = adjacency[v].listIterator();
        while (i.hasNext()) {
            int n = i.next();
            if (!visited[n]) {
                depthFirstSearch(n, visited);
            }
        }
    }

    public static void main(String args[]) {
        Graph g = new Graph(4);

        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);

        // 从顶点2开始
        boolean[] visited = new boolean[g.number];
        g.depthFirstSearch(2, visited);
    }
}

3.3 结果示例

在这里插入图片描述

3.4 过程

1.从顶点2开始搜索，将顶点2标记为已访问
2.获取顶点2可到达的顶点0和顶点3
3.判断顶点0是否已访问，没有访问，则从顶点0开始搜索，将顶点0标记为已访问（从第2点过来的）
4.获取顶点0可到达的顶点1和顶点2（从第3点过来的）
5.判断顶点1是否已访问，没有访问，则从顶点1开始搜索，将顶点1标记为已访问（从第4点过来的）
6.获取顶点1可到达的顶点0和顶点2（从第5点过来的）
7.判断顶点0是否已访问，顶点0已访问（从第6点过来的）
8.判断顶点2是否已访问，顶点2已访问（从第6点过来的）
9.判断顶点2是否已访问，顶点2已访问（从第4点过来的）
10.判断顶点3是否已访问，没有访问，则从顶点3开始搜索，将顶点3标记为已访问（从第2点过来的）
11.获取顶点3可到达的顶点2和顶点3（从第10点过来的）
12.判断顶点2是否已访问，顶点2已访问（从第11点过来的）
13.判断顶点3是否已访问，顶点3已访问（从第11点过来的）

4. 广度优先搜索

4.1 说明

1.Breadth First Search, BFS
2.广度优先遍历图的特点是尽可能先进行横向搜索，即最先访问的顶点的邻接点也先被访问。为此引入队列来保存已访问过的顶点序列，即每当一个顶点被访问后，就将其放入队列中，当队头顶点出队时，就访问其未被访问的邻接点并令这些邻接顶点入队
3.在广度优先遍历算法中，每个顶点最多尽进一次队列
4.遍历图的过程实质上是通过边或弧找邻接点的过程，因此广度优先搜索遍历图和深度优先搜索遍历图的运算时间复杂度相同，其不同之处仅仅在于对顶点访问的次序不同

4.2 步骤

1.图的广度优先搜索方法为：从图中的某个顶点v出发，在访问了v之后依次访问v的各个未被访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问，直到图中所有已被访问的顶点的邻接点都被访问到。若此时还有未被访问的点，则另选图中的一个未被访问的顶点作为起点，重复上述过程，直到图中所有的顶点都被访问到为止

5. 广度优先搜索例子

5.1 无向图

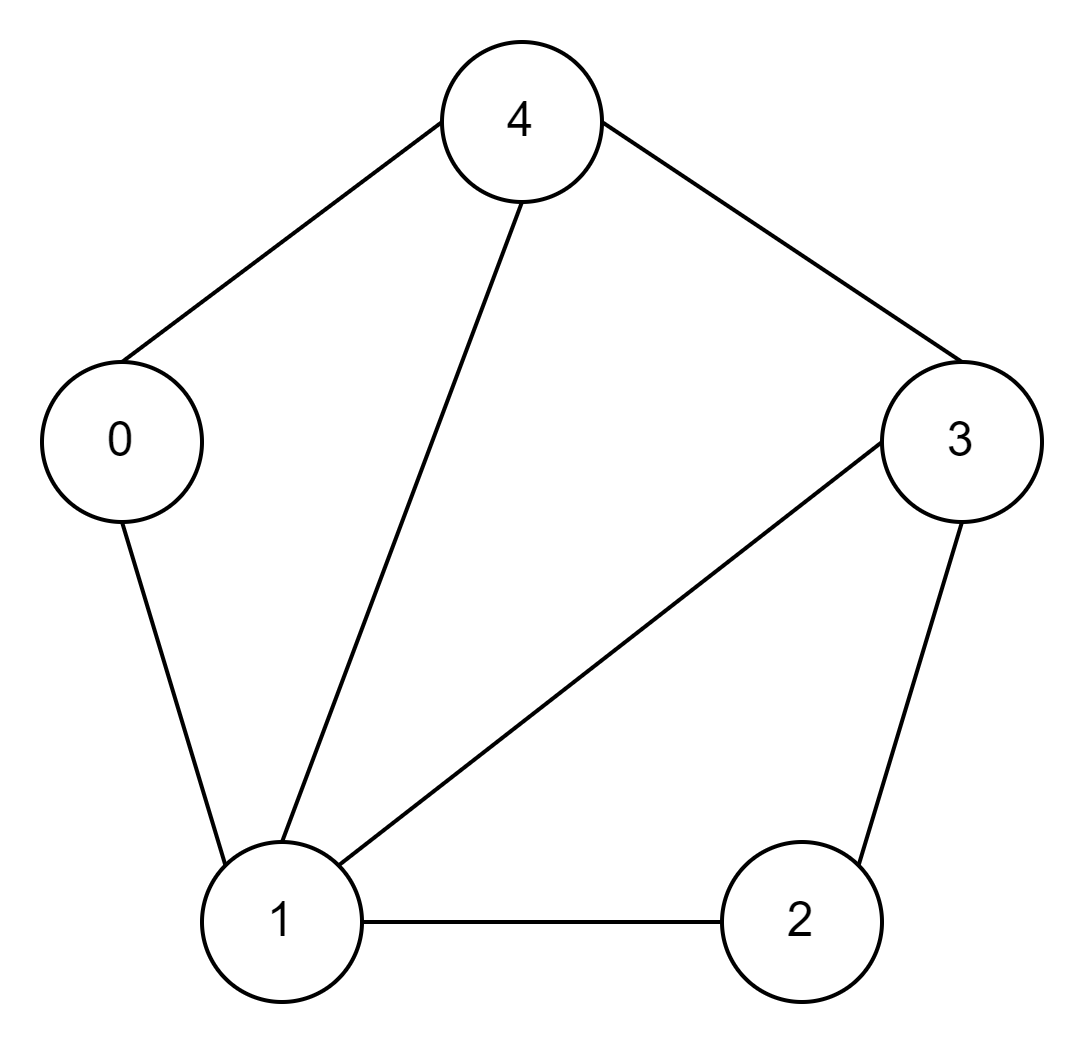
5.2 代码示例

package com.learning.algorithm.search.graph.breadth_first_search;

import java.util.*;
  
public class Graph {
    private int number;
    private LinkedList<Integer>[] adjacency;
  
    public Graph(int number) {
        this.number = number;
        adjacency = new LinkedList[number];
        for (int i = 0; i < number; ++i) {
            adjacency[i] = new LinkedList();
        }
    }

    public void addEdge(int src, int dest) {
        adjacency[src].add(dest);
        // 因为是无向图，所以需要添加反向边
        adjacency[dest].add(src);
    }

    public void breadthFirstSearch(int v) {
        boolean visited[] = new boolean[number];
        Queue<Integer> queue = new LinkedList<>();

        visited[v] = true;
        queue.add(v);

        while (!queue.isEmpty()) {
            int currentVertex = queue.poll();
            System.out.print(currentVertex + " "); // 访问当前节点

            Iterator<Integer> i = adjacency[currentVertex].listIterator();
            while (i.hasNext()) {
                int adjacentVertex = i.next();
                if (!visited[adjacentVertex]) {
                    visited[adjacentVertex] = true;
                    queue.add(adjacentVertex);
                }
            }
        }
    }
  
    public static void main(String args[]) {  
        Graph g = new Graph(7);

        g.addEdge(0, 1);
        g.addEdge(0, 4);
        g.addEdge(1, 2);
        g.addEdge(1, 3);
        g.addEdge(1, 4);
        g.addEdge(2, 3);
        g.addEdge(3, 4);

        g.breadthFirstSearch(0);
    }
}

5.3 结果示例

在这里插入图片描述

5.4 过程

1.从图中的顶点0出发，将顶点0标记为已访问，将顶点0放入队列
2.如果队列不为空，拿出队首顶点0，打印顶点0，获取顶点0可到达的顶点，即顶点1和顶点4
3.顶点1没有被访问，将顶点1标记为已访问，将顶点1放入队列
4.顶点4没有被访问，将顶点4标记为已访问，将顶点4放入队列
5.此时队列不为空，拿出队首顶点1，打印顶点1，获取顶点1可到达的顶点，即顶点0，顶点2，顶点3和顶点4
6.顶点0已经被访问
7.顶点2没有被访问，将顶点2标记为已访问，将顶点2放入队列
8.顶点3没有被访问，将顶点3标记为已访问，将顶点3放入队列
9.顶点4已经被访问
10.此时队列不为空，拿出队首顶点4，打印顶点4，获取顶点4可到达的顶点，即顶点0，顶点1和顶点3
11.顶点0已经被访问
12.顶点1已经被访问
13.顶点3已经被访问
14.此时队列不为空，拿出队首顶点2，打印顶点2，获取顶点2可到达的顶点，即顶点1和顶点3
15.顶点1已经被访问
16.顶点3已经被访问
15.此时队列不为空，拿出队首顶点3，打印顶点3，获取顶点3可到达的顶点，即顶点1，顶点2和顶点4
16.顶点1已经被访问
17.顶点2已经被访问
18.顶点4已经被访问
19.此时队列为空结束

从图中的某个顶点v出发，在访问了v之后依次访问v的各个未被访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问，直到图中所有已被访问的顶点的邻接点都被访问到。若此时还有未被访问的点，则另选图中的一个未被访问的顶点作为起点，重复上述过程，直到图中所有的顶点都被访问到为止

5.5 例题

5.5.1 题目1

1.题目内容

例题1：图G的邻接矩阵如下图所示（顶点依次表示为v0、v1、v2、v3、v4、v5），G是（ 1 ）。
对G进行广度优先遍历（从v0开始），可能的遍历序列为（ 2 ）。
1. 	A.无向图 B.有向图 C.完全图 D.强连通图

2. 	A.v0、v1、v2、v3、v4、v5
	B.v0、v2、v4、v5、v1、v3
	C.v0、v1、v3、v5、v2、v4
	D.v0、v2、v4、v3、v5、v1

2.题目解析

1.由图可以看出，v0可以到达v1和v2，v1可以到达v3，v2可以到达v1和v3，v3可以到达v5，v4可以到达v5
2.部分是单向的因此不是无向图，而是有向图，选B
3.不是完全图（完全图是一个简单的无向图，其中每对不同的顶点之间都恰有一条边相连）
4.不是强连通图（任意两个顶点之间都存在至少一条从一个顶点到另一个顶点的路径，同时也存在至少一条反向的路径）

5.v0可以到v1和v2,则v0、v1、v2，因此选A