目录
详解快速排序
面试题 76 : 数组中第 k 大的数字
详解快速排序
快速排序是一种非常高效的算法,从其名字可以看出这种排序算法最大的特点是快。当表现良好时,快速排序的速度比其他主要对手(如归并排序)快 2 ~ 3 倍。
快速排序的基本思想是分治法,排序过程如下所示:在输入数组中随机选取一个元素作为中间值(pivot),然后对数组进行分区(partition),使所有比中间值小的数据移到数组的左边,所有比中间值大的数据移到数组的右边。接下来对中间值左右两侧的子数组用相同的步骤顺序,直到子数组中只有一个数字为止。
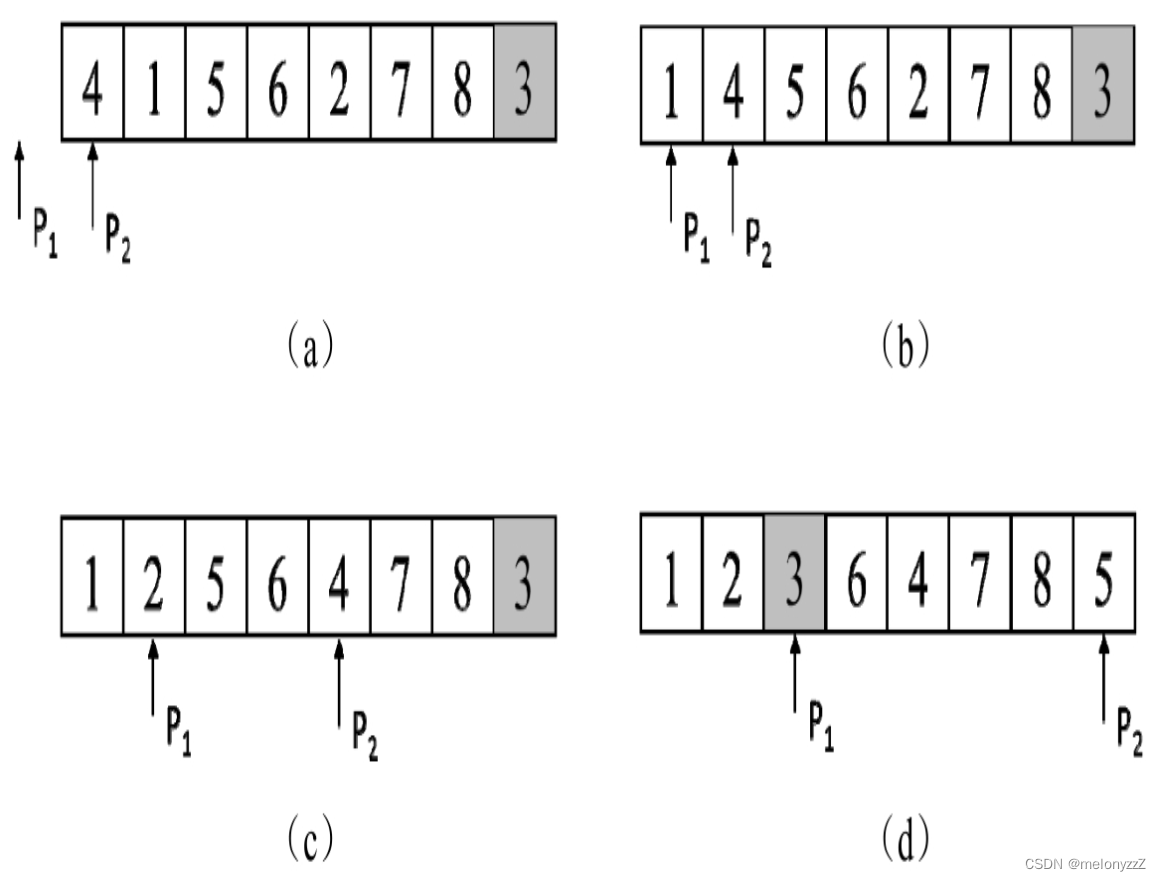
理解快速排序的关键在于理解它的分区的过程。下面以数组 [4, 1, 5, 3, 6, 2, 7, 8] 为例分析分区的过程。假设数字 3 被随机选中为中间值,该数字被交换到数组的尾部。接下来初始化两个指针,指针 P1 初始化至下标为 -1 的位置,指针 P2 初始化至下标为 0 的位置,如下图 (a) 所示。始终将指针 P1 指向已经发现的最后一个小于 3 的数字。此时尚未发现任何一个小于 3 的数字,因此将指针 P1 指向一个无效的位置。将指针 P2 从下标为 0 的位置开始向右扫描数组中的每个数字。当指针 P2 指向第 1 个小于 3 的数字 1 时,指针 P1 向右移动一格,然后交换两个指针指向的数字,此时数组(即两个指针)的状态如下图 (b) 所示。继续向右移动指针 P2 直到遇到下一个小于 3 的数字 2,指针 P1 再次向右移动一格,然后交换两个指针指向的数字,此时数组(即两个指针)的状态如下图 (c) 所示。继续向右移动指针 P2 直到指向数字 3 也没有遇到新的小于 3 的数字,此时整个数组已经扫描完毕。再次将指针 P1 向右移动一格,然后交换指针 P1 和 P2 指向的数字,于是所有小于 3 的数字都位于 3 的左边,所有大于 3 的数字都位于 3 的右边,如下图 (d) 所示。
class Solution {
public:
vector<int> sortArray(vector<int>& nums) {
srand((unsigned int)time(0));
quickSort(nums, 0, nums.size() - 1);
return nums;
}
private:
void quickSort(vector<int>& nums, int left, int right) {
if (left >= right)
return;
int pivotLoc = partition(nums, left, right);
quickSort(nums, left, pivotLoc - 1);
quickSort(nums, pivotLoc + 1, right);
}
int partition(vector<int>& nums, int left, int right) {
int random = left + rand() % (right - left + 1);
swap(nums[random], nums[right]);
int prev = left - 1, cur = left;
while (cur < right)
{
if (nums[cur] < nums[right] && ++prev != cur)
swap(nums[prev], nums[cur]);
++cur;
}
++prev;
swap(nums[prev], nums[right]);
return prev;
}
};快速排序的时间复杂度取决于所选取的中间值在数组中的位置。如果每次选取的中间值在排序数组中都接近于数组中间的位置,那么快速排序的时间复杂度是 O(nlogn)。如果每次选取的中间值都位于排序数组的头部或尾部,那么快速排序的时间复杂度是 O(n^2)。这也是随机选取中间值的原因,避免在某些情况下快速排序退化成时间复杂度为 O(n^2) 的算法。由此可知,在随机选取中间值的前提下,快速排序的平均复杂度是 O(nlogn),是非常高效的排序算法。
很多面试官喜欢要求应聘者手写快速排序算法的代码,因此应聘者需要深刻理解快速排序的思想及分区的过程,这样在遇到要求手写快速排序的代码时也能心中有底。另外,快速排序中的 partition 函数还经常被用来选中数组中第 k 大的数字,而这也是一道非常经典的算法面试题。
面试题 76 : 数组中第 k 大的数字
题目:
请从一个乱序数组中找出第 k 大的数字。例如,数组 [3, 1, 2, 4, 5, 5, 6] 中第 3 大的数字是 5。
分析:
面试题 59 中介绍过一种基于最小堆的解法,该解法的时间复杂度是 O(nlogk)。下面介绍一种更快的解法。
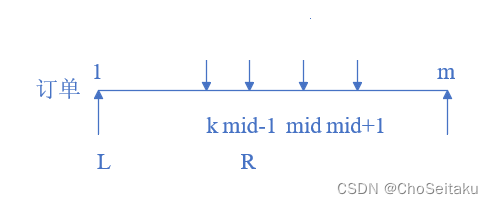
在长度为 n 的排序数组中,第 k 大的数字的下标是 n - k。下面用快速排序的函数 partition 对数组进行分区。
-
如果函数 partition 选取的中间值在分区之后的下标正好是 n - k,分区后左边的值都比中间值小,右边的值都比中间值大,即使整个数组不是排序的,中间值也肯定是第 k 大的数字。
-
如果函数 partition 选取的中间值在分区之后的下标大于 n - k,那么第 k 大的数字一定位于中间值的左侧,于是再对中间值左侧的子数组分区。
-
如果函数 partition 选取的中间值在分区之后的下标小于 n - k,那么第 k 大的数字一定位于中间值的右侧,于是再对中间值右侧的子数组分区。
代码实现:
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
srand((unsigned int)time(0));
int target = nums.size() - k;
int left = 0, right = nums.size() - 1;
int pivotLoc = partition(nums, left, right);
while (pivotLoc != target)
{
if (pivotLoc < target)
left = pivotLoc + 1;
else
right = pivotLoc - 1;
pivotLoc = partition(nums, left, right);
}
return nums[pivotLoc];
}
private:
int partition(vector<int>& nums, int left, int right) {
int random = left + rand() % (right - left + 1);
swap(nums[random], nums[right]);
int prev = left - 1, cur = left;
while (cur < right)
{
if (nums[cur] < nums[right] && ++prev != cur)
swap(nums[prev], nums[cur]);
++cur;
}
++prev;
swap(nums[prev], nums[right]);
return prev;
}
};由于函数 partition 随机选择中间值,因此它的返回值也具有随机性,计算这种算法的时间复杂度需要运用概率相关的知识。此处仅计算一种特定场合下的时间复杂度。假设函数 partition 每次选择的中间值都位于分区后的数组的中间的位置,那么第 1 次函数 partition 需要扫描长度为 n 的数组,第 2 次需要扫描长度为 n/2 的子数组,第 3 次需要扫描 n/4 的子数组,重复这个过程,直到子数组的长度为 1。由于 n + n/2 + n/4 + ··· + 1 = 2n,因此总的时间复杂度是 O(n)。