目录
引言
一、动态规划的基本概念
二、动态规划的应用
1. 背包问题
2. 最短路径问题
3. 0-1背包问题的变种
4. 字符串匹配与编辑距离
5. 金融投资组合优化
6. 生产调度问题
7. 项目管理中的资源分配
三、动态规划算法的优缺点
优点
1 效率高
2 通用性强
缺点:
1 空间复杂度较高
2 设计难度较大
四、结论
引言
在计算机科学中,动态规划是一种重要的算法设计技术,主要用于解决最优化问题。通过存储子问题的解并在需要时重新使用,动态规划显著减少了冗余计算,从而提高了算法的效率。本文将对动态规划的基本概念、应用以及优缺点进行详细的阐述。
一、动态规划的基本概念
动态规划是一种在数学、管理科学和计算机科学中使用的,通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。在求解过程中,动态规划算法将每个子问题的解存储在表格中,以便在需要时直接查找,从而避免了重复计算。
动态规划算法的基本步骤包括:
- 描述问题的最优解的结构;
- 递归地定义最优解的值;
- 自底向上地计算最优解的值;
- 根据计算得到的信息构造一个最优解。
二、动态规划的应用
def knapsack(W, wt, val, n):
# 初始化dp数组,所有元素为0
dp = [0 for w in range(W + 1)]
# 遍历每个物品
for i in range(n):
# 遍历每个可能的承重
for w in range(wt[i], W + 1):
# 更新dp数组的值
dp[w] = max(dp[w], dp[w - wt[i]] + val[i])
# 返回最大价值
return dp[W]
# 测试数据
val = [60, 100, 120] # 物品价值
wt = [10, 20, 30] # 物品重量
W = 50 # 背包最大承重
n = len(val) # 物品数量
# 调用函数并打印结果
print(knapsack(W, wt, val, n)) # 输出:220
假设我们有一个背包,其最大承重为W。我们有一组物品,每个物品都有自己的重量w[i]和价值v[i]。我们需要选择若干物品放入背包中,使得背包内物品的总价值最大,同时不超过背包的总承重。
这个问题可以使用动态规划来解决。我们定义一个数组dp,其中dp[i]表示在承重为i的情况下,能够获得的最大价值。然后,我们遍历每个物品,对于每个物品,我们更新dp数组的值。
请注意,这只是一个简单的示例,用于说明动态规划算法的基本思想。在实际应用中,动态规划算法可能会涉及更复杂的问题和数据结构。
动态规划算法在实际应用中具有广泛的用途,它能够帮助我们解决许多复杂的问题。以下是一些动态规划的实际应用案例:
1. 背包问题
背包问题是一类典型的动态规划问题。假设有一组物品,每种物品都有自己的重量和价值,现在给定一个背包的总承重能力,要求选择若干物品放入背包中,使得背包内物品的总价值最大,同时不超过背包的总承重能力。通过动态规划,我们可以有效地解决这类问题。
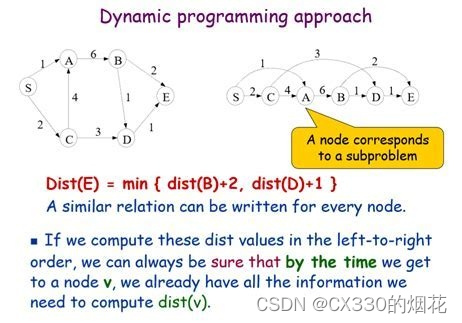
2. 最短路径问题
在图论中,最短路径问题是一个经典问题。给定一个带权图(顶点间连接线的权值代表两点之间的距离或耗费等),找到从源点到目标点的最短路径。例如,在地图导航中,动态规划算法可以帮助我们找到从起点到终点的最快路线。
3. 0-1背包问题的变种
在有些场景中,背包问题可能会有所变种。比如,有的物品是不可分割的,只能选择放入或不放入背包,这种问题通常称为0-1背包问题。而有些物品则是可以分割的,可以选择放入背包的部分数量,这类问题则称为分数背包问题。动态规划算法同样适用于这些变种问题。
4. 字符串匹配与编辑距离
在生物信息学和自然语言处理中,我们经常需要比较两个字符串的相似度。编辑距离(也称为Levenshtein距离)是一种衡量两个字符串差异的度量方式,它表示将一个字符串转换成另一个字符串所需的最少单字符编辑(插入、删除或替换)次数。通过动态规划,我们可以高效地计算出两个字符串之间的编辑距离。
5. 金融投资组合优化
在金融领域,动态规划算法可以用于解决投资组合优化问题。假设投资者有一笔资金,需要在多种投资产品(如股票、债券、基金等)中进行分配,以最大化预期收益或最小化风险。动态规划可以帮助投资者找到最优的投资组合策略。
6. 生产调度问题
在生产制造领域,动态规划算法可以用于解决生产调度问题。例如,一个工厂需要生产多种产品,每种产品都需要经过多个生产阶段,每个阶段都需要一定的时间和资源。通过动态规划,工厂可以优化生产调度,以最小化生产成本或最大化生产效率。
7. 项目管理中的资源分配
在项目管理中,经常需要面对资源有限的情况,如人力、时间、资金等。动态规划可以帮助项目经理在多个项目之间合理分配资源,以实现整体效益的最大化。
这些只是动态规划算法的一些应用案例,实际上,动态规划在各个领域都有广泛的应用,它已经成为解决复杂问题的有力工具之一。
三、动态规划算法的优缺点
优点
1 效率高
通过存储和重用子问题的解,动态规划避免了大量重复计算,从而显著提高了算法的效率。
2 通用性强
动态规划算法适用于多种具有重叠子问题和最优子结构性质的问题,具有较强的通用性。
缺点:
1 空间复杂度较高
动态规划算法需要存储子问题的解,因此空间复杂度可能较高,尤其当问题规模较大时。
2 设计难度较大
动态规划算法的设计需要对问题进行深入的分析和理解,找出问题的最优子结构和重叠子问题,设计合适的状态转移方程。
四、结论
动态规划算法是一种强大的算法设计技术,能够有效地解决具有重叠子问题和最优子结构性质的问题。
通过存储和重用子问题的解,动态规划显著提高了算法的效率。虽然动态规划算法的空间复杂度较高且设计难度较大,但其广泛的应用和高效的性能使得它成为计算机科学领域的重要工具。随着计算机技术的不断发展,动态规划算法将在更多领域发挥重要作用。