直角坐标系下二重积分

助记1：

因为一重积分求出的是二维平面的面积，类比得到二重积分得到的是三维的体积

而用之前求旋转体体积的思路：已知截面面积可求得体积。来表示二重积分

在控制一个变量不变（x / y）时，得到另一个变量的上下界（这个界一般与我们控制的变量有关）

然后在三维中，这个截面积高的函数其实就是被积函数 f(x,y)，所以可以得到这个截面积的表示方法（用一重积分表示）

得到截面积，再利用先前的知识，找到截面积是关于哪个变量变化的，求出变化范围，对其积分就得到最后的结果

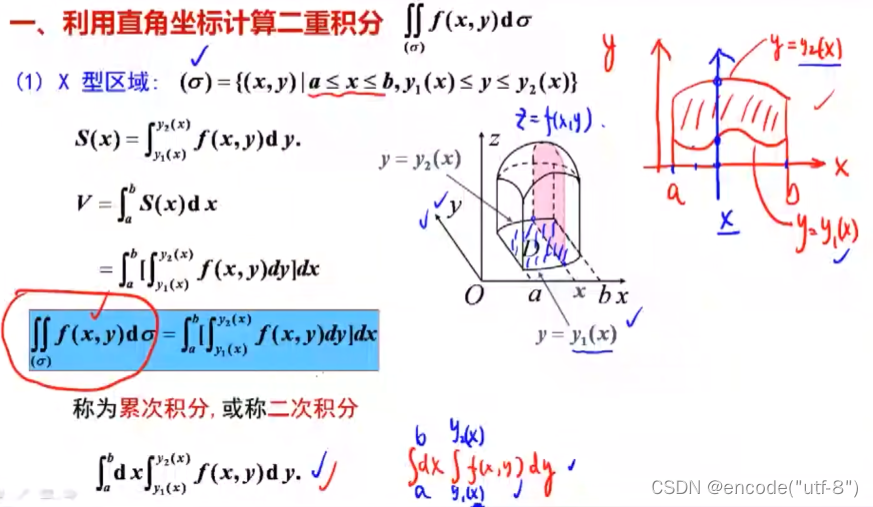
助记2：

通过题目应该可以看出，二重积分计算主要步骤是求积分区域，

找到x，y的变化关系，可以通过一个简单的坐标系画出来

可以根据曲线的复杂程度取舍X型或者Y型方法

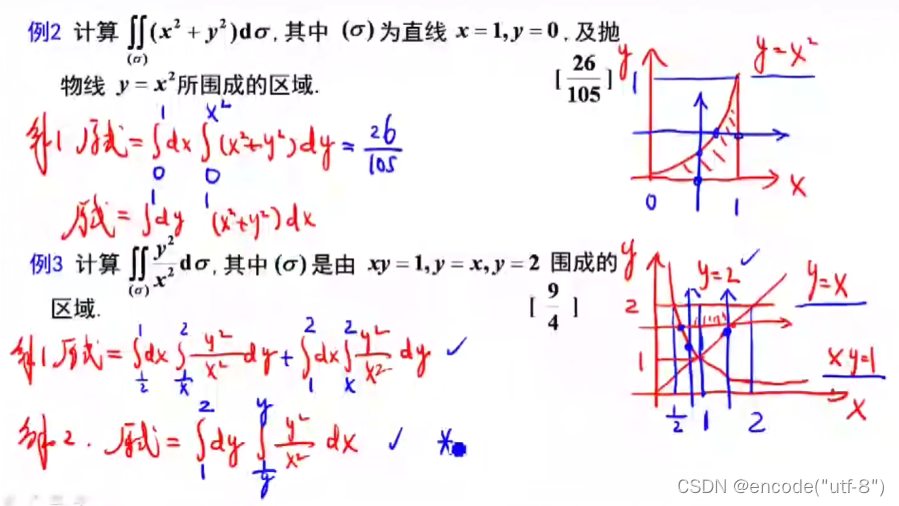
助记3：

有时可能两种方法都能找出积分式子，但有难易之分

而有的题可能某一种形式的积分式无法求解，这时要考虑另外一种写法

---

---

极坐标下二重积分

助记4：

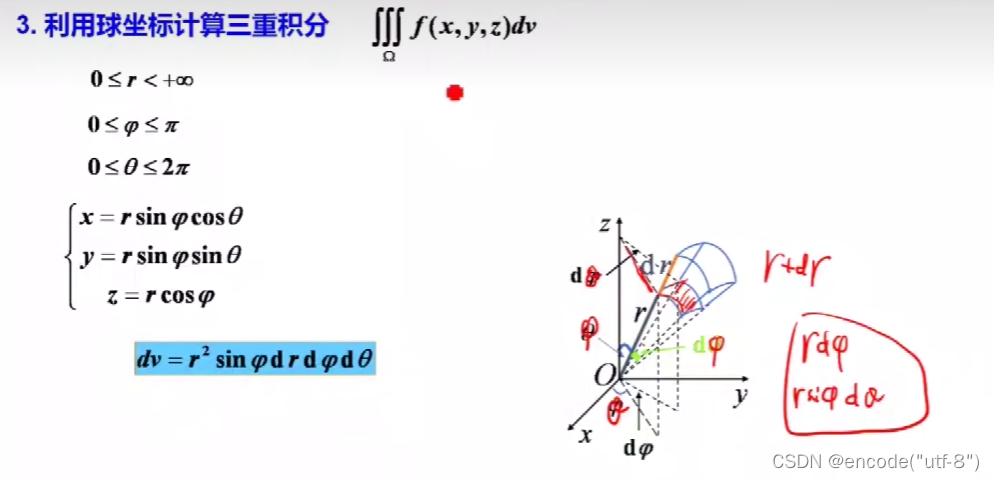
极坐标下我们主要的处理先是对面积微元进行计算

得到了一个近似的估计值如上图（dδ = ρdρdθ）

剩下的过程就是找ρ和θ的范围，一般θ都很容易找出来，而对ρ积分时则需要简单计算

助记5：

在积分时要利用到几何关系确定上下限，

因为使用极坐标往往和圆相关，不要忽略圆内的相关性质

助记6：

这里是用二重积分证明了一个概率论当中的重要结论

要求的域是一个正方形域，而它可以放缩为两个紧紧夹住的圆域

对圆域我们可以利用极坐标很容易得到积分结果

而对正方形域积分时由于可以拆成两个互不相关，形式相同的积分式，所以得到这个结果是以平方形式出现

对积分上限求极限，再代回原不等式，由夹逼定理得到最终结果并开方

---

---

三重积分

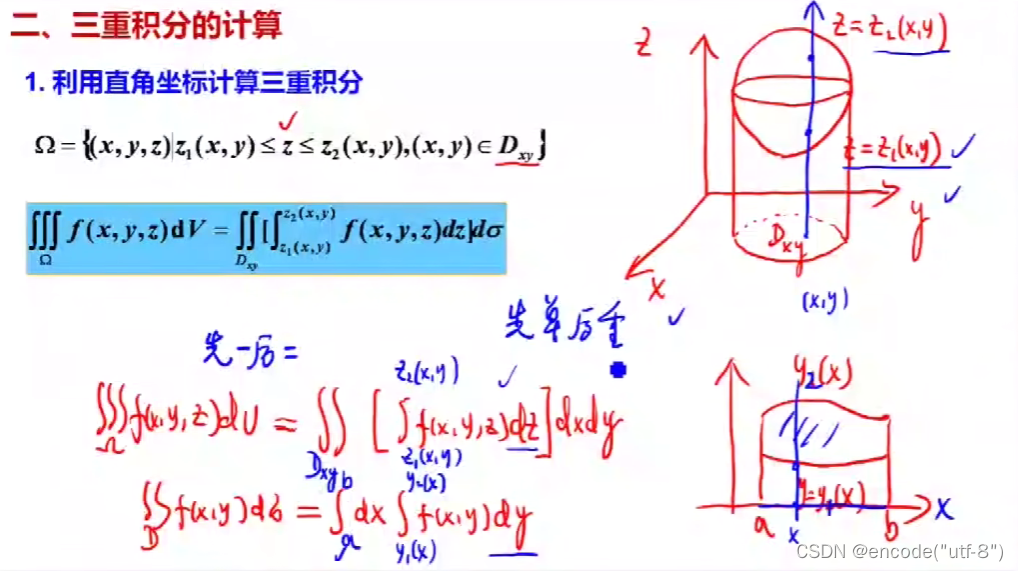
助记7：

先理解三重积分的物理意义：对二重积分（体积）再对某变量积分，这里可以想到是密度。那么乘出来的就是质量

对这个积分过程，其实就是在求一个密度不均匀的物体的质量

根据一重积分和二重积分，三重积分也可以拆分成多次积分，对先拆开的量，根据该变量对应的轴的方向确定上下限：举例——如果先对z求积分，那么沿着z轴方向，由下往上可以得到上下限，这个一般可以由含x与y的式子表示出来，积完以后就可以按照对x，y的二重积分来求解

助记8：

我觉得这道题是能很好帮助我们理解三重积分做法的一道题，

首先我们要能大致画出图形，确定z的上下限分别为什么，然后求出对应的 xy 域

最后由于各种x^2+y^2的出现，让我们想到利用极坐标求二重积分

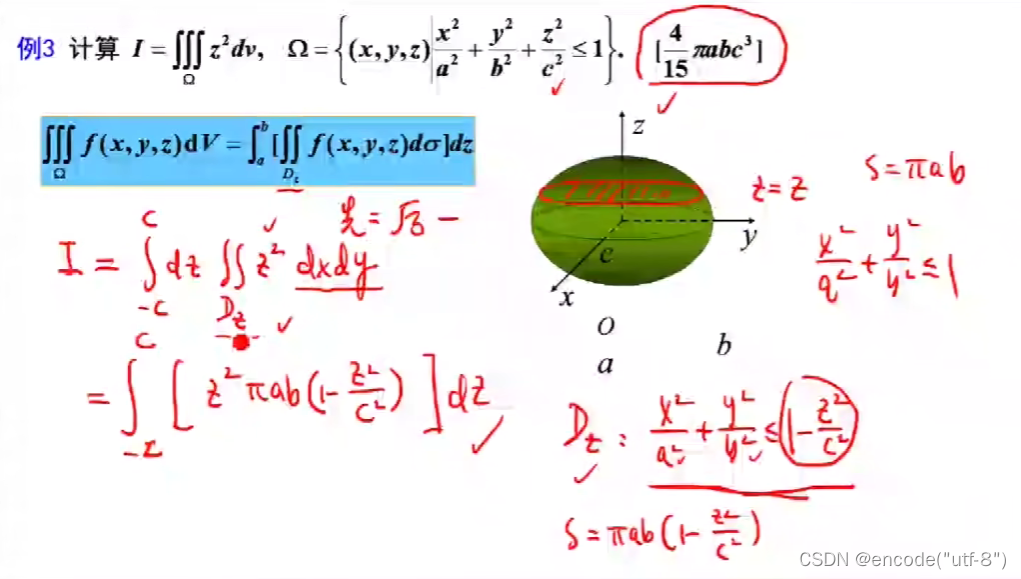
助记9：

对常数求积分就是求积分域的面积，这里采用先对x,y一起求二重积分，再对z求积分

同时直接利用了椭圆的面积公式，可以相比常规先一后二更加快速简洁

助记10：

这种形式的极坐标其实就是只对x,y进行了替换，积分微元也只多乘了一个ρ

计算方法也就是对ρ、θ、z分别找出积分域并积分

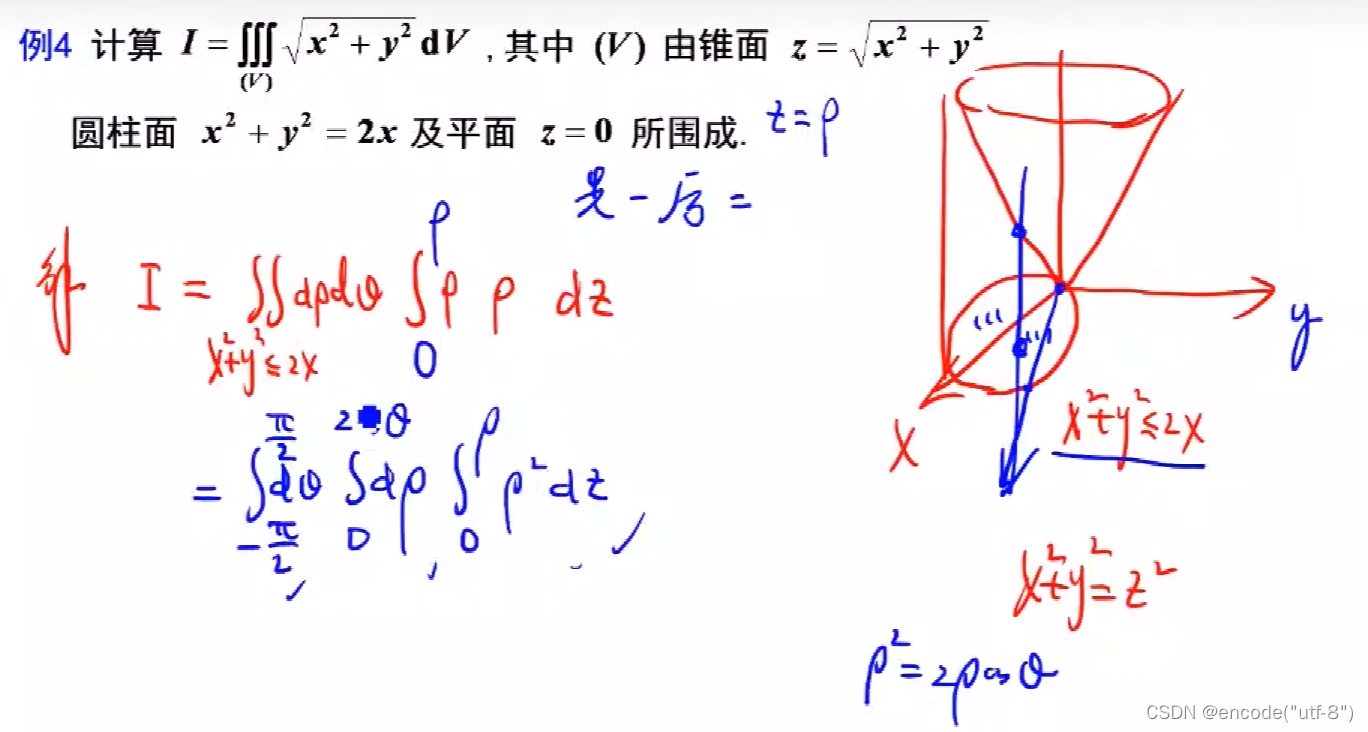
助记11：

这种题一定要将图的位置关系描述准确，不然很可能找错上下限