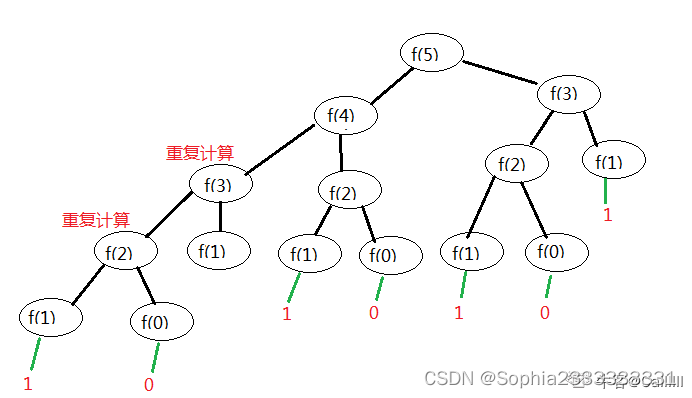
62 斐波那契数列

public class Solution {
    public int Fibonacci(int n) {      
        return f(n);
    }
    public int f(int n){
        if(n==1||n==2){
            return 1;
        }
        return f(n-1)+f(n-2);
    }
}

这种做法时间复杂度O(2^N),空间复杂度是用递归栈，O(n)

改进：用动态规划，可以节省递归栈

public class Solution {
    int[] dp = new int[41];
    public int Fibonacci(int n) {   
        dp[1]=1;dp[2]=1;   
        for(int i=3;i<=n;i++){
            dp[i]= dp[i-1]+dp[i-2];
        }
        return dp[n];
    } 
}

更进一步：每次递归其实只用到前两个，之前都没用，所以只用三个变量存

public class Solution {
    public int Fibonacci(int n) {   
        int a=1;
        int b=1;   
        int c=0;
        if(n<3) return 1;
        for(int i=3;i<=n;i++){
            c=a+b;
            a = b;
            b = c;
        }   
        return c;
    }  
}

时间复杂度O（n）,空间复杂度O(1)

64最小花费爬楼梯

step 1：可以用一个数组记录每次爬到第i阶楼梯的最小花费，然后每增加一级台阶就转移一次状态，最终得到结果。
step 2：（初始状态） 因为可以直接从第0级或是第1级台阶开始，因此这两级的花费都直接为0.
step 3：（状态转移） 每次到一个台阶，只有两种情况，要么是它前一级台阶向上一步，要么是它前两级的台阶向上两步，因为在前面的台阶花费我们都得到了，因此每次更新最小值即可，转移方程为：

dp[i]=min(dp[i−1]+cost[i−1],dp[i−2]+cost[i−2])

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param cost int整型一维数组 
     * @return int整型
     */
     
    public int minCostClimbingStairs (int[] cost) {
        // write code here
        int[] dp = new int[cost.length+1];
        for(int i=2;i<=cost.length;i++){
            dp[i] = Math.min(dp[i-2]+cost[i-2],dp[i-1]+cost[i-1]);
        }
        return dp[cost.length];

    }
}

时间复杂度：O(n)，其中n为给定的数组长度，遍历一次数组
空间复杂度：O(n)，辅助数组dp的空间

65 最长公共子序列2

注意：子序列不是子串，子串要求所有字符必须连续，子序列不要求连续，只要求相对位置不变）

具体做法：

• 优先检查特殊情况。
• 获取最长公共子序列的长度可以使用动态规划，我们以dp[i][j]表示在s1中以iii结尾，s2中以jjj结尾的字符串的最长公共子序列长度。
• 遍历两个字符串的所有位置，开始状态转移：若是iii位与jjj位的字符相等，则该问题可以变成1+dp[i−1][j−1]，即到此处为止最长公共子序列长度由前面的结果加1。
• 若是不相等，说明到此处为止的子串，最后一位不可能同时属于最长公共子序列，毕竟它们都不相同，因此我们考虑换成两个子问题，dp[i][j−1]或者dp[i−1][j]，我们取较大的一个就可以了，由此感觉可以用递归解决。
• 但是递归的复杂度过高，重复计算了很多低层次的部分，因此可以用动态规划，从前往后加，由此形成一个表，表从位置1开始往后相加，正好符合动态规划的转移特征。
• 因为最后要返回该序列，而不是长度，所以在构造表的同时要以另一个二维矩阵记录上面状态转移时选择的方向，我们用1表示来自左上方，2表示来自左边，3表示来自上边。
• 获取这个序列的时候，根据从最后一位开始，根据记录的方向，不断递归往前组装字符，只有来自左上的时候才添加本级字符，因为这种情况是动态规划中两个字符相等的情况，字符相等才可用。

import java.util.*;


public class Solution {
    /**
     * longest common subsequence
     * @param s1 string字符串 the string
     * @param s2 string字符串 the string
     * @return string字符串
     */
     private String x="";
    public String ans(int i,int j,int[][]sign){
        String res = "";
        if(i==0||j==0) return res;
        if(sign[i][j]==1){ 
            res+=ans(i-1,j-1,sign); 
            //如果把这两个顺序调过来 答案就是倒序的
            res+=x.charAt(i-1);        
        }
        else if(sign[i][j]==2){
            res+=ans(i-1,j,sign);
        }
        else if(sign[i][j]==3){
            res+=ans(i,j-1,sign);
        }
        return res;
    }
    public String LCS (String s1, String s2) {
        // write code here
        x = s1;//搞个全局的，让外面的也能用
        if(s1.length()==0||s2.length()==0) return "-1";
        int[][] dp = new int[s1.length()+1][s2.length()+1];
        int[][] sign = new int[s1.length()+1][s2.length()+1];
        for(int[] t:dp){
            Arrays.fill(t,0);
        }
        for(int i=1;i<=s1.length();i++){
            for(int j=1;j<=s2.length();j++){
                if(s1.charAt(i-1)==s2.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+1;
                    sign[i][j] = 1;//左上角 
                }else if(dp[i-1][j]>dp[i][j-1]){
                    dp[i][j] = dp[i-1][j];
                    sign[i][j]=2;//上面
                }else{
                    dp[i][j] = dp[i][j-1];
                    sign[i][j]=3;//左边
                }
            }
        }
        String res = ans(s1.length(),s2.length(),sign);
        if(res.length()==0) return "-1";
        return new String(res);
    }
}

66最长公共子串

子串就说明是连续的，比上一题更简单一点，不用去标记方向

import java.util.*;


public class Solution {
    /**
     * longest common substring
     * @param str1 string字符串 the string
     * @param str2 string字符串 the string
     * @return string字符串
     */
    public String LCS (String str1, String str2) {
        // write code here
        int len1 = str1.length();
        int len2 = str2.length();
        int[][] dp = new int[len1+1][len2+1];
        for(int[] tmp: dp){
            Arrays.fill(tmp,0);
        }
        int max = Integer.MIN_VALUE;
        int re = -1;
        for(int i = 1;i<=len1;i++){
            for(int j=1;j<=len2;j++){
                if(str1.charAt(i-1)==str2.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+1;
                }//没有就不用干了
                if(dp[i][j]>max){
                    max=dp[i][j];
                    re= i;//记下最长的位置
                }
            }
        }      
        // String res="";
        // for(int i=re-max;i<re;i++){
        //     res+=Character.toString(str1.charAt(i));
        // }
        // return res;
        return str1.substring(re-max,re);

    }
}

str1.substring(re-max,re);//直接获取子串

67 不同路径的数目

step 1：用dp[i][j]表示大小为i∗j的矩阵的路径数量，下标从1开始。
step 2：（初始条件） 当i或者j为1的时候，代表矩阵只有一行或者一列，因此只有一种路径。
step 3：（转移方程） 每个格子的路径数只会来自它左边的格子数和上边的格子数，因此状态转移为dp[i][j]=dp[i−1][j]+dp[i][j−1]

import java.util.*;


public class Solution {
    /**
     * 
     * @param m int整型 
     * @param n int整型 
     * @return int整型
     */
    public int uniquePaths (int m, int n) {
        // write code here
        int[][] dp = new int[m+1][n+1];
        for(int[] tmp:dp){
            Arrays.fill(tmp,1);
        }
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(i==0&&j==0){                 
                }else if(i==0){
                    dp[i][j]=dp[i][j-1];
                }else if(j==0){
                    dp[i][j]=dp[i-1][j];
                }else
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        
        return dp[m-1][n-1];
    }
}

68 矩阵的最小路径和

import java.util.*;


public class Solution {
    /**
     * 
     * @param matrix int整型二维数组 the matrix
     * @return int整型
     */
    public int minPathSum (int[][] matrix) {
        // write code here
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] dp = new int[m][n];
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(i==0&&j==0) dp[i][j]=matrix[i][j];
                else if(i==0) dp[i][j]=matrix[i][j]+dp[i][j-1];
                else if(j==0) dp[i][j]=matrix[i][j]+dp[i-1][j];
                else dp[i][j]=matrix[i][j]+Math.min(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[m-1][n-1];
    }
}

69 将数字翻译成字符串

我觉得这个题目没有写得很清楚，比如302其实是0种，02不能算一种，我觉得这个需要说清楚。多种情况讨论主要针对0的出现

step 1：用辅助数组dp表示前i个数的译码方法有多少种。
step 2：对于一个数，我们可以直接译码它，也可以将其与前面的1或者2组合起来译码：如果直接译码，则dp[i]=dp[i−1]；如果组合译码，则dp[i]=dp[i−2]。
step 3：对于只有一种译码方式的，选上种dp[i−1]即可，对于满足两种译码方式（10，20不能）则是dp[i−1]+dp[i−2]
step 4：依次相加，最后的dp[length]即为所求答案。

import java.util.*;


public class Solution {
    /**
     * 解码
     * @param nums string字符串 数字串
     * @return int整型
     */
    public int solve (String nums) {
        // write code here
        if(nums.charAt(0)=='0') return 0;
        //特殊情况
        else if(nums.equals("10")||nums.equals("20")) return 1;
        int n=nums.length();
        int[] dp=new int[n+1];
        Arrays.fill(dp,1);
                
        for(int i=2;i<=n;i++){
            //当0的前面不是1或2时，无法译码，0种
            if(nums.charAt(i-1)=='0'){
                if(nums.charAt(i-2)!='1'&&nums.charAt(i-2)!='2') return 0;
                dp[i]=dp[i-1];           
            }//11-19,21-26
            else if((nums.charAt(i-2)=='1'&& nums.charAt(i - 1) != '0')||(nums.charAt(i-2)=='2'&&nums.charAt(i-1)<'7')){               
                dp[i]=dp[i-1]+dp[i-2];             
            }
            else{
                dp[i]=dp[i-1];
            } 
        }
        return dp[n];
    }
}

70 兑换零钱（一）

step 1：可以用dp[i]表示要凑出i元钱需要最小的货币数。
step 2：一开始都设置为最大值aim+1，因此货币最小1元，即货币数不会超过aim.
step 3：初始化dp[0]=0。
step 4：后续遍历1元到aim元，枚举每种面值的货币都可能组成的情况，取每次的最小值即可，转移方程为dp[i]=min(dp[i],dp[i−arr[j]]+1) .
step 5：最后比较dp[aim]的值是否超过aim，如果超过说明无解，否则返回即可。

import java.util.*;


public class Solution {
    /**
     * 最少货币数
     * @param arr int整型一维数组 the array
     * @param aim int整型 the target
     * @return int整型
     */
    public int minMoney (int[] arr, int aim) {
        // write code here
        int[] dp = new int[aim+1];
        Arrays.fill(dp,aim+1);
        //很重要
        dp[0] = 0;
        for(int i=1;i<=aim;i++){
            for(int j=0;j<arr.length;j++){
                if(arr[j]<=i) dp[i] = Math.min(dp[i],dp[i-arr[j]]+1);
            }
        }
        return dp[aim]>aim?-1:dp[aim];
    }
}

71 最长上升子序列

一开始认为只要判断当前元素和上一个元素的大小即可，后来发现不行，dp[i]表示以当前arr[i]为结尾的最长上升子序列的长度，因此每计算一个dp需要找到之前小的且dp最大的，需遍历一遍，所以是O(N2)

step 1：用dp[i]表示到元素iii结尾时，最长的子序列的长度，初始化为1，因为只有数组有元素，至少有一个算是递增。
step 2：第一层遍历数组每个位置，得到n个长度的子数组。
step 3：第二层遍历相应子数组求对应到元素iii结尾时的最长递增序列长度，期间维护最大值。
step 4：对于每一个到iii结尾的子数组，如果遍历过程中遇到元素j小于结尾元素，说明以该元素结尾的子序列加上子数组末尾元素也是严格递增的，因此转移方程为dp[i]=dp[j]+1。

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 给定数组的最长严格上升子序列的长度。
     * @param arr int整型一维数组 给定的数组
     * @return int整型
     */
    public int LIS (int[] arr) {
        // write code here
        int n = arr.length;
        if(n==0) return 0;
        int[] dp = new int[n+1];
        Arrays.fill(dp,1);
        int res = 1;
        for(int i=1;i<n;i++){
            //找到之前比它小的且dp最大的 
            for(int j=i-1;j>=0;j--){                 
                if(arr[i]>arr[j]&&dp[j]>dp[i]-1){
                    dp[i]=dp[j]+1;
                    res = Math.max(res,dp[i]);
                }
            }
        }   
        return res;
    }
}

72 连续子数组的最大和

public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
        if(array.length==1) return array[0];
        int res=Integer.MIN_VALUE;
        int before = 0;
        int tmp=0;
        for(int i=0;i<array.length;i++){
            tmp=Math.max(before,0)+array[i];//之前的和若<0，可换成0
            res=Math.max(res,tmp);
            before=tmp;
        }
        return res;        
    }
}

时间复杂度O(n),空间复杂度O(1)

73 最长回文子串

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param A string字符串 
     * @return int整型
     */
    public int getLongestPalindrome (String A) {
        // write code here
        int max=0;
        for(int i=0;i<A.length();i++){
            max = Math.max(max,Math.max(func(A,i,i),func(A,i,i+1)));
        }
        return max;
    }
    public int func(String str,int begin,int end){
        //int count=0;
        while(begin<=end&&begin>=0&&end<str.length()&&str.charAt(begin)==str.charAt(end)){
            begin--;
            end++;
        }
        return end-begin-1;//出来的时候begin和end是不符合条件的，要-2
    }
}

中心扩展法

具体做法：

step 1：遍历字符串每个字符。
step 2：以每次遍历到的字符为中心（分奇数长度和偶数长度两种情况），不断向两边扩展。
step 3：如果两边都是相同的就是回文，不断扩大到最大长度即是以这个字符（或偶数两个）为中心的最长回文子串。
step 4：我们比较完每个字符为中心的最长回文子串，取最大值即可。

时间复杂度：O(n^2)，其中n为字符串长度，遍历字符串每个字符，每个字符的扩展都要O(n)
空间复杂度：O(1)，常数级变量，无额外辅助空间

74 数字字符串转化成IP地址

import java.util.*;


public class Solution {
    /**
     * 
     * @param s string字符串 
     * @return string字符串ArrayList
     */
    public ArrayList<String> restoreIpAddresses (String s) {
        // write code here
        ArrayList<String> res = new ArrayList<String>();
        for(int i=0;i<s.length()-3;i++){
            for(int j=i+1;j<s.length()-2;j++){
                for(int k=j+1;k<s.length()-1;k++){
                    if(s.length()-k>4) continue;//最后超过3位
                    String s1 = s.substring(0,i+1);
                    String s2 = s.substring(i+1,j+1);
                    String s3 = s.substring(j+1,k+1);
                    String s4 = s.substring(k+1,s.length());

                    //去掉前面的0的判断
                    if(Integer.parseInt(s1)>256||Integer.parseInt(s1)<0||(Integer.parseInt(s1)==0&&s1.length()>1)||(Integer.parseInt(s1)!=0&&s1.charAt(0)=='0')) continue;
                    if(Integer.parseInt(s2)>256||Integer.parseInt(s2)<0||(Integer.parseInt(s2)==0&&s2.length()>1)||(Integer.parseInt(s2)!=0&&s2.charAt(0)=='0')) continue;
                    if(Integer.parseInt(s3)>256||Integer.parseInt(s3)<0||(Integer.parseInt(s3)==0&&s3.length()>1)||(Integer.parseInt(s3)!=0&&s3.charAt(0)=='0')) continue;
                    if(Integer.parseInt(s4)>256||Integer.parseInt(s4)<0||(Integer.parseInt(s4)==0&&s4.length()>1)||(Integer.parseInt(s4)!=0&&s4.charAt(0)=='0')) continue;
            
                    res.add(s1+"."+s2+"."+s3+"."+s4);
                }
            }
        }
        return res;
    }
}

时间复杂度：如果将3看成常数，则复杂度为O(1)，如果将3看成字符串长度的1/4，则复杂度为O(n^3)，三次嵌套循环
空间复杂度：如果将3看成常数，则复杂度为O(1)，如果将3看成字符串长度的1/4，则复杂度为O(n)，4个记录截取字符串的临时变量。res属于返回必要空间。

回溯

import java.util.*;
public class Solution {
    //记录分段IP数字字符串
    private String nums = ""; 
    //step表示第几个数字，index表示字符串下标
    public void dfs(String s, ArrayList<String> res, int step, int index){ 
        //当前分割出的字符串
        String cur = ""; 
        //分割出了四个数字
        if(step == 4){ 
            //下标必须走到末尾
            if(index != s.length()) 
                return;
            res.add(nums);
        }else{
            //最长遍历3位
            for(int i = index; i < index + 3 && i < s.length(); i++){ 
                cur += s.charAt(i);
                //转数字比较
                int num = Integer.parseInt(cur); 
                String temp = nums;
                //不能超过255且不能有前导0
                if(num <= 255 && (cur.length() == 1 || cur.charAt(0) != '0')){ 
                    //添加点
                    if(step - 3 != 0) 
                        nums += cur + ".";
                    else
                        nums += cur;
                    //递归查找下一个数字
                    dfs(s, res, step + 1, i + 1); 
                    //回溯
                    nums = temp; 
                }
            }
        }
    }
    public ArrayList<String> restoreIpAddresses (String s) {
        ArrayList<String> res = new ArrayList<String>();
        dfs(s, res, 0, 0);
        return res;
    }
}

75 编辑距离

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param str1 string字符串 
     * @param str2 string字符串 
     * @return int整型
     */
    public int editDistance (String str1, String str2) {
        // write code here
        int m = str1.length();
        int n = str2.length();
        //dp[i][j]表示到str1[i]和str2[j]为止的子串需要的编辑距离
        int[][] dp = new int[m+1][n+1];
        for(int[] tmp:dp){
            Arrays.fill(tmp,0);
        }
        //初始化边界
        for(int i = 1; i <= m; i++)
            dp[i][0] = dp[i - 1][0] + 1;
        for(int i = 1; i <= n; i++)
            dp[0][i] = dp[0][i - 1] + 1;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                
                if(str1.charAt(i-1)==str2.charAt(j-1)) dp[i][j]=dp[i-1][j-1];
                else
                 dp[i][j]=Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i][j-1]))+1;

                // System.out.print(dp[i][j]+" ");
            }
            //System.out.println();
        }
        return dp[m][n];
    }
}

step 1：初始条件： 假设第二个字符串为空，那很明显第一个字符串子串每增加一个字符，编辑距离就加1，这步操作是删除；同理，假设第一个字符串为空，那第二个字符串每增加一个字符，编剧距离就加1，这步操作是添加。
step 2：状态转移： 状态转移肯定是将dp矩阵填满，那就遍历第一个字符串的每个长度，对应第二个字符串的每个长度。如果遍历到str1[i]和 str2[j]的位置，这两个字符相同，这多出来的字符就不用操作，操作次数与两个子串的前一个相同，因此有dp[i][j]=dp[i−1][j−1]；如果这两个字符不相同，那么这两个字符需要编辑，但是此时的最短的距离不一定是修改这最后一位，也有可能是删除某个字符或者增加某个字符，因此我们选取这三种情况的最小值增加一个编辑距离，即dp[i][j]=min(dp[i−1][j−1],min(dp[i−1][j],dp[i][j−1]))+1。

注意是三种情况！！！取最小的。时间和空间复杂度都是O(MN)

76 正则表达式匹配

每个字符有三种情况出现：“字符”、.、*
**状态定义：**dp[i][j]表示字符串 str的前 i 个字符串和 pattern 的前 j 个字符串是否匹配
**状态转移：主要是对*的状态处理
当 pattern[i - 1] != *，即上一位不为。dp[i][j]在以下任何一种情况为true时，则等于true
1、dp[i - 1][j - 1] && str[i - 1] == pattern[j - 1]，即上一个状态和当前位的字符都匹配
2、dp[i - 1][j - 1] && pattern[j - 1] == ‘.’，即上一个状态为true，且pattern上一位包含 ‘.’
当 pattern[i - 1] == *，即当前位的上一位为。dp[i][j]在以下任何一种情况为true时，则等于true
1、dp[i][j - 2]，即 j-2 位 的pattern能满足，则 i-1 位是*作为任意数量的值必定能满足匹配
2、dp[i - 1][j] && str[i - 1] == pattern[j - 2]；即让字符 pattern[j-2]多出现几次，看能否匹配
3、dp[i - 1][j] && pattern[j - 2] ==., 即让字符. 多出现 1 次时，能否匹配；
状态初始化
dp[0][0] == true： 代表两个空字符串能够匹配。
dp[0][j] = dp[0][j - 2] 且 p[j - 1] = *, 即当前pattern的0到j位是true还是false，取决于dp[0][j-2]是否匹配，以及 pattern的当前位的上一位是否为*，因为‘*’可以匹配任何值，包括空值
返回值
dp 矩阵右下角字符，代表字符串 str 和 pattern 能否匹配

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param str string字符串 
     * @param pattern string字符串 
     * @return bool布尔型
     */
    public boolean match (String str, String pattern) {
        // write code here
        int m = str.length();
        int n = pattern.length();
        boolean dp[][] = new boolean[m+1][n+1];//注意不是Boolean
        dp[0][0] = true;
        //初始化首行
        for(int j=2;j<=n;j++){
            if(pattern.charAt(j-1)=='*') dp[0][j]=dp[0][j-2];
        }
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                //不考虑*刚好匹配
                if(pattern.charAt(j-1)=='.'||str.charAt(i-1)==pattern.charAt(j-1))
                    dp[i][j]=dp[i-1][j-1];
                    //考虑*
                else if(j>=2&&pattern.charAt(j-1)=='*'){
                    if(pattern.charAt(j-2)==str.charAt(i-1)||pattern.charAt(j-2)=='.'){
                        dp[i][j]=dp[i][j-2]||dp[i-1][j]||dp[i-1][j-2];
                    }else{
                        dp[i][j]=dp[i][j-2];
                    }
                }
            }
        }
        return dp[m][n];
    }
}

77 最长的括号子串

step 1：可以使用栈来记录左括号下标。
step 2：遍历字符串，左括号入栈，每次遇到右括号则弹出左括号的下标。
step 3：然后长度则更新为当前下标与栈顶下标的距离。
step 4：遇到不符合的括号，可能会使栈为空，因此需要使用start记录上一次结束的位置，这样用当前下标减去start即可获取长度，即得到子串。
step 5：循环中最后维护子串长度最大值。

import java.util.*;
public class Solution {
    public int longestValidParentheses (String s) {
        int res = 0;
        //记录上一次连续括号结束的位置
        int start = -1; 
        Stack<Integer> st = new Stack<Integer>();
        for(int i = 0; i < s.length(); i++){
            //左括号入栈
            if(s.charAt(i) == '(') 
                st.push(i);
            //右括号
            else{ 
                //如果右括号时栈为空，不合法，设置为结束位置
                if(st.isEmpty()) 
                    start = i;
                else{
                    //弹出左括号
                    st.pop(); 
                    //栈中还有左括号，说明右括号不够，减去栈顶位置就是长度
                    if(!st.empty()) 
                        res = Math.max(res, i - st.peek());
                    //栈中没有括号，说明左右括号行号，减去上一次结束的位置就是长度
                    else 
                        res = Math.max(res, i - start);
                }
            }
        }
        return res;
    }
}

78 打家劫舍一

step 1：用dp[i]表示长度为i的数组，最多能偷取到多少钱，只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。
step 2：（初始状态） 如果数组长度为1，只有一家人，肯定是把这家人偷了，收益最大，因此dp[1]=nums[0]。
step 3：（状态转移） 每次对于一个人家，我们选择偷他或者不偷他，如果我们选择偷那么前一家必定不能偷，因此累加的上上级的最多收益，同理如果选择不偷他，那我们最多可以累加上一级的收益。因此转移方程为dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度，在nums中为下标。

import java.util.*;
public class Solution {
    public int rob (int[] nums) {
        //dp[i]表示长度为i的数组，最多能偷取多少钱
        int[] dp = new int[nums.length + 1]; 
        //长度为1只能偷第一家
        dp[1] = nums[0]; 
        for(int i = 2; i <= nums.length; i++)
            //对于每家可以选择偷或者不偷
            dp[i] = Math.max(dp[i - 1], nums[i - 1] + dp[i - 2]); 
        return dp[nums.length];
    }
}

时间和空间复杂度都是O(n)

79 打家劫舍二

step 1：使用原先的方案是：用dp[i]表示长度为i的数组，最多能偷取到多少钱，只要每次转移状态逐渐累加就可以得到整个数组能偷取的钱。

step 2：（初始状态） 如果数组长度为1，只有一家人，肯定是把这家人偷了，收益最大，因此dp[1]=nums[0]。

step 3：（状态转移） 每次对于一个人家，我们选择偷他或者不偷他，如果我们选择偷那么前一家必定不能偷，因此累加的上上级的最多收益，同理如果选择不偷他，那我们最多可以累加上一级的收益。因此转移方程为dp[i]=max(dp[i−1],nums[i−1]+dp[i−2])。这里的i在dp中为数组长度，在nums中为下标。

step 4：此时第一家与最后一家不能同时取到，那么我们可以分成两种情况讨论：

情况1：偷第一家的钱，不偷最后一家的钱。初始状态与状态转移不变，只是遍历的时候数组最后一位不去遍历。
情况2：偷最后一家的请，不偷第一家的钱。初始状态就设定了dp[1]=0，第一家就不要了，然后遍历的时候也会遍历到数组最后一位。
step 5：最后取两种情况的较大值即可。

import java.util.*;
public class Solution {
    public int rob (int[] nums) {
        //dp[i]表示长度为i的数组，最多能偷取多少钱
        int[] dp = new int[nums.length + 1]; 
        //选择偷了第一家
        dp[1] = nums[0]; 
        //最后一家不能偷
        for(int i = 2; i < nums.length; i++) 
            //对于每家可以选择偷或者不偷
            dp[i] = Math.max(dp[i - 1], nums[i - 1] + dp[i - 2]); 
        int res = dp[nums.length - 1]; 
        //清除dp数组，第二次循环
        Arrays.fill(dp, 0); 
        //不偷第一家
        dp[1] = 0; 
        //可以偷最后一家
        for(int i = 2; i <= nums.length; i++) 
            //对于每家可以选择偷或者不偷
            dp[i] = Math.max(dp[i - 1], nums[i - 1] + dp[i - 2]); 
        //选择最大值
        return Math.max(res, dp[nums.length]); 
    }
}

80 买卖股票的最好时机(一)

只要找到出现过的最低的股票价格，然后减去即可

import java.util.*;


public class Solution {
    /**
     * 
     * @param prices int整型一维数组 
     * @return int整型
     */
    public int maxProfit (int[] prices) {
        // write code here
        int min = Integer.MAX_VALUE;//前面出现过的最小
        int res = -1;
        int n = prices.length;
        if(n<=1) return 0;
        for(int i=0;i<n;i++){
            if(prices[i]<min) min = prices[i];
            res = Math.max(res,prices[i]-min);
        }
        return res;
    }
}

买卖股票的最好时机(二)

只要把每次中间的差值加起来即可
用dp数组的话

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 计算最大收益
     * @param prices int整型一维数组 股票每一天的价格
     * @return int整型
     */
    public int maxProfit (int[] prices) {
        // write code here
        int n = prices.length;
        if(n==1) return 0;
        int[] dp = new int[n+1];
        Arrays.fill(dp,0);
        for(int i=2;i<=n;i++){
            dp[i] = dp[i-1]+Math.max(0,prices[i-1]-prices[i-2]);
        }
        return dp[n];
    }
}

空间复杂度O(n),也可以不用数组

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 计算最大收益
     * @param prices int整型一维数组 股票每一天的价格
     * @return int整型
     */
    public int maxProfit (int[] prices) {
        // write code here
        int n = prices.length;
        if(n==1) return 0;
        int res=0;
        for(int i=1;i<n;i++){
            res = res+Math.max(0,prices[i]-prices[i-1]);
        }
        return res;
    }
}

82 买卖股票的最好时机（三）

dp[i][0]表示到第i天为止没有买过股票的最大收益
dp[i][1]表示到第i天为止买过一次股票还没有卖出的最大收益
dp[i][2]表示到第i天为止买过一次也卖出过一次股票的最大收益
dp[i][3]表示到第i天为止买过两次只卖出过一次股票的最大收益
dp[i][4]表示到第i天为止买过两次同时也买出过两次股票的最大收益

step 1：（初始状态） 与上述提到的题类似，第0天有买入了和没有买两种状态：dp[0][0]=0、dp[0][1]=−prices[0]。
step 2：状态转移： 对于后续的每一天，如果当天还是状态0，则与前一天相同，没有区别；
step 3：如果当天状态为1，可能是之前买过了或者当天才第一次买入，选取较大值：dp[i][1]=max(dp[i−1][1],dp[i−1][0]−prices[i])；
step 4：如果当天状态是2，那必须是在1的状态下（已经买入了一次）当天卖出第一次，或者早在之前就卖出只是还没买入第二次，选取较大值：dp[i][2]=max(dp[i−1][2],dp[i−1][1]+prices[i])；
step 5：如果当天状态是3，那必须是在2的状态下（已经卖出了第一次）当天买入了第二次，或者早在之前就买入了第二次，只是还没卖出，选取较大值：dp[i][3]=max(dp[i−1][3],dp[i−1][2]−prices[i])
step 6：如果当天是状态4，那必须是在3的状态下（已经买入了第二次）当天再卖出第二次，或者早在之前就卖出了第二次，选取较大值：dp[i][4]=max(dp[i−1][4],dp[i−1][3]+prices[i])。
step 7：最后我们还要从0、第一次卖出、第二次卖出中选取最大值，因为有可能没有收益，也有可能只交易一次收益最大。

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 两次交易所能获得的最大收益
     * @param prices int整型一维数组 股票每一天的价格
     * @return int整型
     */
    public int maxProfit (int[] prices) {
        // write code here
        int n = prices.length;
        int[][] dp = new int[n+1][5];
        for(int[] tmp:dp) Arrays.fill(tmp,0);
        dp[0][1] = -prices[0];
        dp[0][3] = -prices[0];  
        for(int i=1;i<=n;i++){
            dp[i][0] = dp[i-1][0];
            dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i-1]);
            dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]+prices[i-1]);
            dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]-prices[i-1]);
            dp[i][4] = Math.max(dp[i-1][4],dp[i-1][3]+prices[i-1]);
        }
        //可以只操作一次
        return Math.max(dp[n][2],dp[n][4]);
    }
}