1. 独立均匀分布

matlab的rand指令可以帮助我们生成[0,1]的均匀分布的数据，这样，如果我们想要[a,b]的分布数据，只需要a+(b-a)*rand就可以了。

[a,b] 均值μ，标准差

均值

标准差

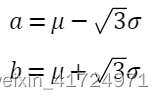
matlab代码：

%% 生成一个n行p列的矩阵
% A = rand(n,p);
% 生成1000行1列，[0,1]的随机数，均值为0.5，方差为1/12.
A=rand(1000,1);
muA=mean(A)
sigmaA = std(A)
% 生成1000行1列，[5,10]的随机数
% B = a+(b-a)*rand(n,1)
B=5+(10-5)*rand(1000,1);
muB=mean(B)
sigmaB=std(B)
% 生成1000行1列，均值为10，方差为10的随机数：
C=10-sqrt(3)*10+(10+sqrt(3)*10-10+sqrt(3)*10).*rand(1000,1);
muC=mean(C)
sigmaC=std(C)

2. 3D\2D-PPP泊松点分布

在Matlab的环境下，matlab自带一维poisson点生成函数：poissrnd(lambda,m,n)

一维的Poisson过程和Poisson分布，从时间的角度似乎更加容易解释：事件发生的次数，两件事情发生的平均间隔时间服从指数分布。

对于2维或者三维来说，即：随机抽样出来的样本点在范围内服从均匀分布，样本点之间的距离服从指数分布.

注释-指数分布：指数分布，可以用来表示独立随机事件发生的时间间隔。

指数分布的参数为λ，则指数分布的期望为，方差为。

“Two distinct ways can be used to generate realisations of homogeneous Poisson process. One is to use the property that the spatial differences (areas in 2D case) between successive point events follow an exponential distribution with parameter λ (the density of the Poisson process). Different implementations can be derived to explore this property in 2D and 3D cases. The other way is to simulate the Poisson variable N(A) directly. Simulation of N(A) may sometimes be time-consuming, the implementation nevertheless is simpler and less error prone. In the current exercise, direct Poisson variable simulation is used.”
————————————————
版权声明：本文为CSDN博主「weixin_38206454」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接： 3D-PPP分布，2D-PPP分布的Matlab实现_weixin_38206454的博客-CSDN博客_数学ppp分布是什么

仿真上可以使用两种不同的方式来产生均匀泊松过程的实现：