目录
题目链接:505. 火柴排队 - AcWing题库
解题思路:
离散化:
归并排序求逆序对:
总代码:
题目链接:505. 火柴排队 - AcWing题库
涵涵有两盒火柴,每盒装有 n 根火柴,每根火柴都有一个高度。
现在将每盒中的火柴各自排成一列,同一列火柴的高度互不相同,两列火柴之间的距离定义为:
其中 ai 表示第一列火柴中第 i 个火柴的高度,bi 表示第二列火柴中第 i 个火柴的高度。
每列火柴中相邻两根火柴的位置都可以交换,请你通过交换使得两列火柴之间的距离最小。
请问得到这个最小的距离,最少需要交换多少次?
如果这个数字太大,请输出这个最小交换次数对 99,999,997 取模的结果。
输入格式
共三行,第一行包含一个整数 n,表示每盒中火柴的数目。
第二行有 n 个整数,每两个整数之间用一个空格隔开,表示第一列火柴的高度。
第三行有 n 个整数,每两个整数之间用一个空格隔开,表示第二列火柴的高度。
输出格式
输出共一行,包含一个整数,表示最少交换次数对 99,999,997 取模的结果。
数据范围
1≤n≤10^5,
0≤火柴高度≤2^31−1,
输入样例:
4
2 3 1 4
3 2 1 4
输出样例:
1
解题思路:
离散化+归并排序求逆序对(或者树状数组求逆序对)
树状数组比较抽象,这里以归并排序为例。先听我阐述一下大体思路,后面细节听我娓娓道来。这个题一看无非是交换序列最小次数,如果我们固定第一组数据,那么第二组数据就按照第一组的数据大小排列即可保证最小距离,那么我们把第一组数据排一下序,第二组的数据是不是就好处理了。由于数据量很大,且数据不集中很离散,可能会爆栈,考虑离散化。那么我们把数组a,b都处理好了下面考虑移动几次就好了。根据结论,一个数组b中的元素移动到另一个数组a使其位置相同,最少需要移动b的逆序对数(前提是排好序),那么我们如何求逆序对呢,想一想归并排序的实现,可以利用前面数组l的数l[i]大于后面数组r的数r[j]的特点,若前面数组l的数l[i]大于后面数组r的数r[j],说明数组l此时位置i往后到mid的位置都是逆序对数,因为数组l是有序的,既然此时的位置i都要大于数组r的数r[j],那么l[i]到l[mid]都是大于r[j]的,那么逆序对数就是mid-i+1,总的逆序对数即为答案。
离散化:
离散化,把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。
通俗的说,离散化是在不改变数据相对大小的条件下,对数据进行相应的缩小。例如:
原数据:1,999,100000,15;处理后:1,3,4,2;
什么时候使用离散化,当数据很离散且很大,当要去此值当作数组下标,例如n<=1e5;0<=a[i]<=1e9。
下面写一个模板
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+5;
const int M=1e9+5;
int a[N];
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
sort(a+1,a+n+1);//排序
int len=unique(a+1,a+n+1)-(a+1);//去重,len为新长度
for(int i=1;i<=len;i++){
cout<<a[i]<<" ";//排序好的数据
a[i]=lower_bound(a+1,a+n+1,a[i])-a;
cout<<a[i]<<endl;//离散化映射下标
}
return 0;
}
归并排序求逆序对:
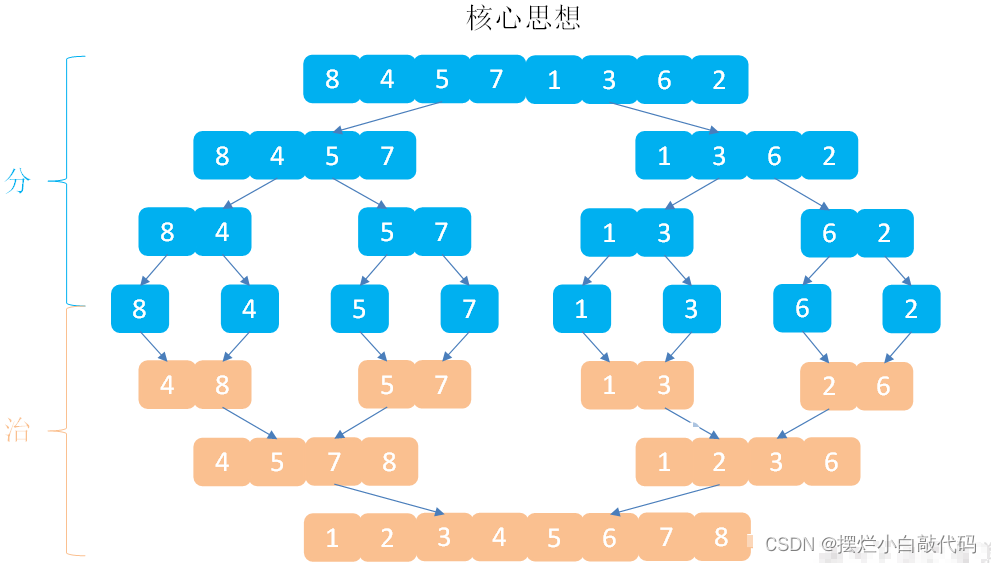
下面写一下求逆序对函数:
int merge_sort(int l,int r){
if(l>=r)return 0;
int mid=l+r>>1;
int res=(merge_sort(l,mid)+merge_sort(mid+1,r))%mod;
int i=l,j=mid+1,k=0;
while(i<=mid&&j<=r){
if(b[i]<=b[j])p[k++]=b[i++];
else p[k++]=b[j++],res=(res+mid-i+1)%mod;
}//只有前面数组大于后面数组的数时,才满足逆序对
while(i<=mid)p[k++]=b[i++];
while(j<=r)p[k++]=b[j++];
for(int i=l,j=0;i<=r;i++,j++)b[i]=p[j];
return res;
}总代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int mod=99999997;
const int N=1e5+5;
int n;
int a[N],b[N],c[N],p[N];
int find(int x){//二分查找
int l=1,r=n;
while(l<r){
int mid=l+r>>1;
if(p[mid]>=x)r=mid;
else l=mid+1;
}
return l;
}
void work(int a[]){//离散化函数
for(int i=1;i<=n;i++)p[i]=a[i];
sort(p+1,p+n+1);
for(int i=1;i<=n;i++){
a[i]=find(a[i]);
//a[i]=lower_bound(p+1,p+n+1,a[i])-p;可以用lower_bound函数更简单
}
return;
}
int merge_sort(int l,int r){//归并求逆序对
if(l>=r)return 0;
int mid=l+r>>1;
int res=(merge_sort(l,mid)+merge_sort(mid+1,r))%mod;
int i=l,j=mid+1,k=0;
while(i<=mid&&j<=r){
if(b[i]<=b[j])p[k++]=b[i++];
else p[k++]=b[j++],res=(res+mid-i+1)%mod;
}
while(i<=mid)p[k++]=b[i++];
while(j<=r)p[k++]=b[j++];
for(int i=l,j=0;i<=r;i++,j++)b[i]=p[j];
return res;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)cin>>b[i];
work(a),work(b);
for(int i=1;i<=n;i++)c[a[i]]=i;
for(int i=1;i<=n;i++)b[i]=c[b[i]];
cout<<merge_sort(1,n)<<endl;
return 0;
}此题比较抽象,需要很多转化处理,可以看一看B站的讲解,笔者写可能有不准确的地方,一些地方也不是最优解法,望大家理解,若有错误请大家指出共同进步。