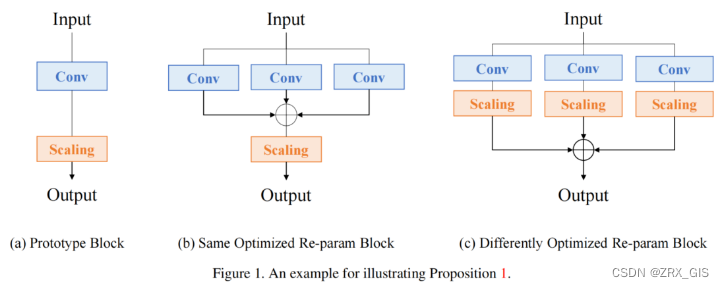
图 1. 除了关节的极端变异性外,许多关节几乎不可见。我们能猜测左图中右臂的位置,因为我们看到了姿势的其余部分,并预测了这个人的运动或活动。同样,右边的人的左半身也根本看不见。这些都是需要进行整体推理的例子。我们相信DNNs可以很正确地进行这种类型的推理。
Abstract
我们提出了一种基于深度神经网络(DNNs)的人体姿态估计方法。姿态估计被表述为一个基于DNN的身体关节回归问题。我们提出了一连串的DNN回归器,以输出高精度的姿态估计。该方法的优势是以一种整体的方式推理姿势,有一个简单但强大的公式,利用了深度学习的最新进展。我们提出了一个详细的实证分析,在各种真实图像的四个学术基准上具有最新或更好的性能。
Introduction
人体姿态估计问题,被定义为人体关节的定位问题,在计算机视觉界引起了广泛的关注。在图 1中,我们可以看到这个问题的一些挑战——大关节、小的几乎不可见的关节、遮挡和捕获背景。
该领域的主流工作主要是由第一个挑战推动的,即需要在大空间中寻找所有可能的关节姿态。基于部分的模型使他们自然的模仿关节连接,并且近年来也提出了各种具有有效推理的模型。
然而,上述的效率是以表达的限制为代价实现的——使用局部检测器,这在许多情况下是关于单个的,最重要的是可以仅通过对身体部分之间的所有交互的一小部分进行建模。如图1所示,这些局限性已被认识到,并提出了以整体方式推理姿势的方法,但在现实问题中取得的成功也是有限的。
在这项工作中,我们归纳了人类姿态估计的整体观点。我们利用深度学习的最新发展,提出了一种基于深度神经网络(DNN)的新算法。DNNs在视觉分类任务[14]和最近在对象定位[23,9]上表现出了出色的表现。然而,应用dnn精确定位铰接物体的问题在很大程度上仍然没有得到解答。在本文中,我们试图阐明这个问题,并基于DNN提出简单而强大的整体人体姿态估计方法。
在这项工作中,我们归纳了人类姿态估计的整体观点。我们利用深度学习的最新发展,提出了一种基于深度神经网络(DNN)的新算法。DNN在视觉分类任务和最近在对象定位上表现出了出色的性能。然而,应用DNN精确定位关节物体的问题在很大程度上仍未得到解答。在本文中,我们试图阐明这个问题,并提出一个类似DNN的,简单而强大的整体人体姿态估计器。
我们将姿态估计表示为一个联合回归问题,并展示了如何成功地在DNN设置中描述它。使用完整图像和7层通用卷积DNN作为输入,回归每个身体关节的位置。这种方法有两个优点。首先,DNN能够捕获每个身体关节的完整背景——每个关节回归器使用完整的图像作为信息。其次,该方法比基于图形模型的方法要简单得多——无需显式设计模型拓扑和关节之间的交互;不需要显式地设计模型拓扑和关节之间的交互。相反,我们证明了可以针对此问题使用通用DNN卷积。
此外,我们提出了一个基于DNN的姿态级联预测器。这种联级(网络的串联)可以提高连接位置的精度。从基于完整图像的初始姿态估计开始,我们学习基于DNN的回归器,它通过使用更高分辨率的子图像来细化联合预测。
我们使用四个广泛使用的基准测试比对所有实验结果,展示了最先进的结果。我们的方法在外表上呈现明显不同的关节的人的图像上也会表现良好。最后,我们通过跨数据集评估来展示泛化性能。
Related Work
从计算机视觉 [16] 的早期提倡将一般的铰接物体,特别是人体姿势表示为零件图的想法。由 Fishler 和 Elschlager 引入的图形结构 ( Pictorial Strictures PS) ,Felzenszwalb 和 Huttenlocher使用距离变换技巧变得易于处理和实用。因此,随后开发了多种具有实际意义的基于 PS 的模型。
然而,上述的可操作性伴随着一个限制,那就是基于树的姿势模型具有简单的二进制潜力,不依赖于图像数据。因此,研究的重点是在保持可操作性的同时丰富模型的表现力。早期实现这一目标的尝试是基于更丰富的部分检测器。
最近,人们提出了各种各样的表达复杂联合关系的模型。Yang和Ramanan使用了一个零件的混合模型。Johnson和Everingham[13]研究了全模型规模的混合模型,通过具有PS的混合。Tian等人[25]在一个分层模型中捕获了更丰富的高阶空间关系。捕捉高阶关系的另一种方法是通过与图像相关的PS模型,它可以通过全局分类器来估计。
我们以整体方式推理姿势的方法显示出有限的实用性。Mori和Malik试图从一组标记的图像中为每张测试图像找到最接近的样本,并转换连接位置。Shakhnarovich等人[21]采用了类似的近邻设置,但他们使用的是位置敏感散列。最近,Gkioxari等人[10]提出了一个用于零件配置的semi-global分类器。这种提法在现实世界的数据上显示出非常好的效果,然而,它是基于线性分类器,其表现力不如我们,而且只在手臂上测试。最后,Ionescu等人[11]采用了姿势回归的思想,然而他们推理的是三维姿态
与我们最接近的工作是使用CNN和邻接成分分析,向代表姿势的嵌入中的一个点回归[24]。然而,这项工作并没有采用级联网络的方式。然而,DNN回归器的级联已经被用于面部点的定位[22]。在脸部姿势估计的相关问题上,Osadchy等人[17]采用了一个基于NN的姿势嵌入,用对比损失进行训练。
Deep Learning Model for Pose Estimation
我们使用以下符号。为了表达一个姿势,我们将所有k个身体关节的位置编码在姿势向量中,定义为 y = ( . . . , y i T . . . ) , i ∈ 1 , . . . , k y = (. . . , y^T_i. . . ), i∈ {1, . . . , k} y=(...,yiT...),i∈1,...,k,其中 y i y_i yi包含第 i i i个关节的 x x x和 y y y坐标。标记的图像用 ( x , y ) (x,y) (x,y)表示,其中x代表图像数据,y是ground truth。
此外,由于关节坐标是绝对图像坐标,因此要将它们标准化为限制人体或其部分的框 b 。在一个简单的情况下,框可以表示完整的图像。这样的方框由其中心
b
c
∈
R
2
b_c\in\R^2
bc∈R2以及宽度
b
w
b_w
bw 和高度
b
h
b_h
bh 定义:
b
=
(
b
c
,
b
w
,
b
h
)
b =(b_c,b_w,b_h)
b=(bc,bw,bh)。然后连接点
y
i
y_i
yi 可以通过框中心进行平移,并通过框大小进行缩放,我们将其称为
b
b
b 的归一化:
N
(
y
i
;
b
)
=
[
1
/
b
w
0
0
1
/
b
h
]
(
y
i
−
b
c
)
(1)
N(y_i;b)=\begin{bmatrix} 1/b_w &0 \\ 0 &1/b_h \end{bmatrix}(y_i-b_c)\tag{1}
N(yi;b)=[1/bw001/bh](yi−bc)(1)
此外,我们对姿态向量
N
(
y
;
b
)
=
(
.
.
.
,
N
(
y
i
;
b
)
T
,
.
.
.
)
T
N(y;b)=(...,N(y_i; b)^T ,...)^T
N(y;b)=(...,N(yi;b)T,...)T 的元素应用相同的归一化,从而得到归一化的姿态矢量。最后,我们使用
N
(
x
;
b
)
N(x; b)
N(x;b) 来表示边界框
b
b
b 对图像 $x $的裁剪,这实际上通过边界框对图像进行了归一化。为简洁起见,我们用
N
(
⋅
)
N(·)
N(⋅) 归一化表示,其中 b 是完整图像框。
3.1. Pose Estimation as DNN-based Regression
在这项工作中,我们将姿态估计视为回归问题,其中我们训练并使用函数
ψ
(
x
;
θ
)
∈
R
2
k
ψ(x;θ)\in R^{2k}
ψ(x;θ)∈R2k,该函数对于图像x回归到归一化的姿态向量,其中θ表示模型的参数。因此,使用等式(1)的归一化变换,绝对图像坐标中的姿势预测
y
∗
y^*
y∗读取
y
1
←
N
−
1
(
ψ
(
N
(
x
;
b
0
)
;
θ
1
)
;
b
0
)
(2)
\quad \mathbf{y}^{1} \leftarrow N^{-1}\left(\psi\left(N\left(x ; b^{0}\right) ; \theta_{1}\right) ; b^{0}\right) \tag{2}
y1←N−1(ψ(N(x;b0);θ1);b0)(2)
尽管其公式简单,但该方法的能力和复杂性是 ψ \psi ψ决定的,他基于卷积深度神经网络(DNN)。这种卷积网络由几层组成,每层都是线性变换,后面是非线性变换。第一层将预定义大小的图像作为输入,其大小等于像素数乘以三个颜色通道。最后一层输出回归的目标值,在我们的例子中是2k个坐标。
我们将
ψ
\psi
ψ的体系结构建立在Krizhevsky等人[14]对图像分类的工作基础上,因为它在对象定位方面也表现出了突出的结果。
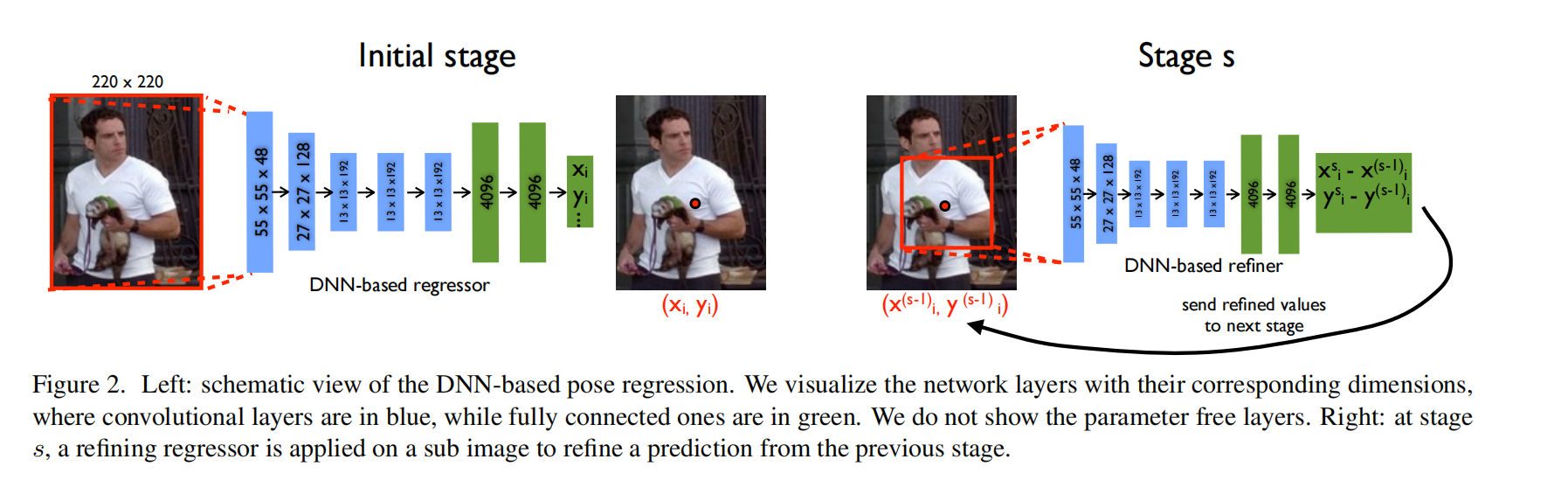
左图:基于DNN的姿态回归示意图。其中卷积层用蓝色表示,全连接层用绿色表示。我们不显示无参数层。右图:在 s 个阶段,将精细化回归应用于子图像以改进前一阶段的预测。
网络由7层组成(见左图2)。用C表示卷积层,用LRN表示局部响应标准化层,用P表示池化层,用F表示全连接层。只有C层和F层包含可学习的参数,而其余的是无参数的。C层和F层都由一个线性变换和一个非线性变换组成,在我们的例子中,非线性变换是一个校正的线性单元。对于C层,尺寸定义为宽度×高度×深度,其中前两个维度具有空间意义,而深度定义了滤波器的数量。如果我们将每层的尺寸写在括号内,那么网络可以简单地描述为 C ( 55 ∗ 55 ∗ 96 ) − L R N − P − C ( 27 ∗ 27 ∗ 256 ) − L R N − P − C ( 13 ∗ 13 ∗ 384 ) − C ( 13 ∗ 13 ∗ 384 ) − C ( 13 ∗ 13 ∗ 256 ) − P − F ( 4096 ) − F ( 4096 ) C(55*55*96)-LRN-P-C(27*27*256)-LRN-P-C(13*13*384)-C(13*13*384)-C(13*13*256)-P-F(4096)-F(4096) C(55∗55∗96)−LRN−P−C(27∗27∗256)−LRN−P−C(13∗13∗384)−C(13∗13∗384)−C(13∗13∗256)−P−F(4096)−F(4096)。前两个C层的滤波器尺寸为11 × 11和5 × 5,其余三层的滤波器尺寸为3 × 3。在三层之后应用池化,尽管分辨率降低,但仍有助于提高性能。网络的输入是一幅220×220×23的图像,它通过步长为4的(卷积),变为55×55×48输入到网络中。上述模型的参数总数约为40M。
在实验部分,我们展示了这样一种通用架构可以用于学习模型,从而在姿态估计方面达到最先进或更好的性能。此外,这样的模型是一个真正的整体模型-最终的关节位置估计是基于完整图像的复杂非线性变换。此外,这样的模型是一个真正的整体模型-最终的联合位置估计基于完整图像的复杂非线性变换。
此外,DNN的使用消除了设计领域特定姿势模型的需要。相反,这种模型和特征是从数据中学习的。虽然回归损失没有模拟关节之间的显式交互,但这是由所有7个隐藏层隐式捕获的——所有关节回归器共享所有内部特征。
Training
我们与图像分类的损失不同。我们在最后一个网络层上训练线性回归,以代替分类损失,通过最小化预测和真实姿态向量之间的
L
2
L_2
L2距离来预测姿势向量。由于ground truth姿态矢量是在绝对图像坐标中定义的,并且姿态在大小上随图像而变化,我们使用等式(1)的归一化来归一化我们的训练集D。
D
N
=
(
N
(
x
)
,
N
(
y
)
)
∣
(
x
,
y
)
∈
D
(3)
D_N = {(N(x), N(y))|(x, y) ∈ D} \tag{3}
DN=(N(x),N(y))∣(x,y)∈D(3)
然后用于获得最佳网络参数的
L
2
L_2
L2损失为:
arg
min
θ
∑
(
x
,
y
)
∈
D
N
∑
i
=
1
k
∥
y
i
−
ψ
i
(
x
;
θ
)
∥
2
2
(4)
\arg \min _{\theta} \sum_{(x, y) \in D_{N}} \sum_{i=1}^{k}\left\|\mathbf{y}_{i}-\psi_{i}(x ; \theta)\right\|_{2}^{2}\tag{4}
argθmin(x,y)∈DN∑i=1∑k∥yi−ψi(x;θ)∥22(4)
为清楚起见,作者写出了对各个关节的优化。应该注意,即使某些图像不是所有关节都被标记,也可以使用上述目的。在这种情况下,将省略总和中的相应项。
上面的参数 θ θ θ是为了在分布式配置中对实现反向传播进行优化。对于每个大小为128的mini-batch,自适应梯度更新计算为[3Adaptive subgradient methods for online learning and stochastic optimization]。学习率作为最重要的参数,设置为0.0005。由于模型参数大,但数据集相对较小,我们使用大量随机图像裁剪,左/右翻转以及F层设置为0.6的DropOut正则化来进行增强数据。
3.2. Cascade of Pose Regressors
级联姿态回归器
前一部分的姿态公式具有以下优点:联合估计基于完整图像并因此依赖于背景。然而,由于其固定输入大小为 220×220,网络查看细节的能力有限——它学习的滤波器以粗略的比例捕获姿态属性。这些粗糙姿态的估计是必要的,但不足以始终精确地定位身体关节。值得注意的是,不能轻易增加输入大小,因为这样将增加已经很多的参数。为了获得更好的精度,我们建议训练一个联级姿态回归器。在第一阶段,级联从估算初始姿态开始,如前一节所述。在随后的阶段,训练附加的DNN回归器来预测从先前阶段到真实位置的关节位置的位移。因此,每个后续阶段可以被认为是当前预测姿态的细化,如图2所示。
此外,每个后续阶段使用预测的关节位置来聚焦于图像的相关部分——围绕来自前一阶段的预测关节位置裁剪子图像,并将该关节的姿态位移回归应用于该子图像。以这种方式,后续的姿态回归器看到更高分辨率的图像,从而学习更精细尺度的特征,这最终实现更高的精度。
我们对级联的所有阶段使用相同的网络架构,但是学习不同的网络参数。对于阶段
s
∈
{
1
,
.
.
.
,
S
}
s ∈\{1, ... ,S\}
s∈{1,...,S} 共 S 个级联阶段,我们用
θ
s
θ_s
θs表示网络的学习参数。因此,姿态位移回归量是
ψ
(
x
;
θ
s
)
ψ(x;θ_s)
ψ(x;θs) 。为了改进给定的关节位置
y
i
y_i
yi,我们将考虑捕获
y
i
y_i
yi周围的子图像的关节边界框
b
i
b_i
bi:
b
i
(
y
;
σ
)
=
(
y
i
,
d
i
a
m
(
y
)
σ
,
d
i
a
m
(
y
)
σ
)
b_i(y;σ)=(y_i,diam(y)σ,diam(y)σ)
bi(y;σ)=(yi,diam(y)σ,diam(y)σ) 以第 i 个坐标作为中心,并且尺度为 σ 。姿态的直径
d
i
a
m
(
y
)
diam(y)
diam(y) 定义为人体躯干上关节之间的相对距离,例如左肩和右臀的距离,这取决于具体的姿态定义和数据集。
S
t
a
g
e
1
:
y
1
←
N
−
1
(
ψ
(
N
(
x
;
b
0
)
;
θ
1
)
;
b
0
)
Stage 1 : \quad \mathbf{y}^{1} \leftarrow N^{-1}\left(\psi\left(N\left(x ; b^{0}\right) ; \theta_{1}\right) ; b^{0}\right)\\
Stage1:y1←N−1(ψ(N(x;b0);θ1);b0)
在每个后续阶段 s ≥ 2 s≥2 s≥2,对于所有关节 i ∈ { 1 , . . . , k } i∈\{1,...,k\} i∈{1,...,k} 我们通过在子图像上应用回归来精细化位置 y i s − y i ( s − 1 ) y_i^s -y_i^{(s−1)} yis−yi(s−1) 。子图像由来自之前 ( s − 1 ) (s-1) (s−1) 层的 b i ( s − 1 ) b_i^{(s−1)} bi(s−1) 定义。然后,作者重新估计方框 b i s b_i^s bis:
S t a g e s : y i s ← y i ( s − 1 ) + N − 1 ( ψ i ( N ( x ; b ) ; θ s ) ; b ) ( 6 ) for b = b i ( s − 1 ) b i s ← ( y i s , σ diam ( y s ) , σ diam ( y s ) ) Stage s: \quad \mathbf{y}_{i}^{s} \leftarrow \mathbf{y}_{i}^{(s-1)}+N^{-1}\left(\psi_{i}\left(N(x ; b) ; \theta_{s}\right) ; b\right)(6) \\ \text { for } b=b_{i}^{(s-1)} \\ b_{i}^{s} \leftarrow\left(\mathbf{y}_{i}^{s}, \sigma \operatorname{diam}\left(\mathbf{y}^{s}\right), \sigma \operatorname{diam}\left(\mathbf{y}^{s}\right)\right) \\ Stages:yis←yi(s−1)+N−1(ψi(N(x;b);θs);b)(6) for b=bi(s−1)bis←(yis,σdiam(ys),σdiam(ys))
我们将级联应用于 S 个阶段,如 4.1节 所述。
Training
网络参数 θ 1 θ_1 θ1 按照第 3.1 节中的公式 (4) 训练。在随后 s ≥ 2 s\geq2 s≥2 的阶段,训练完成相同的微分。来自训练样本 ( x , y ) (x,y) (x,y) 的每个关节 i i i 使用不同的边界框 ( y i ( s − 1 ) , σ d i a m ( y ( s − 1 ) ) , σ d i a m ( y ( s − 1 ) ) ) (y_i^{(s−1)},σ diam(y^{(s−1)}),σ diam(y^{(s−1)})) (yi(s−1),σdiam(y(s−1)),σdiam(y(s−1))) 来标准化——这个边界框是从之前的层次中的相同关节为中心——这样就可以根据前一阶段的模型来调整阶段的训练。
由于深度学习方法要训练很大的体量,我们通过对每个图像和关节使用 multiple normalization 来增加训练数据。作者不仅使用前一阶段的预测,而是生成模拟预测。这是通过从二维正态分布 N i ( s − 1 ) \mathcal N_i^{(s−1)} Ni(s−1)随机抽样的矢量随机移动关节 i i i 的 ground truth 位置来完成的,二维正态分布其均值和方差等于观察到的训练数据中的偏置量 ( y i ( s − 1 ) − y i ) ( y i ( s − 1 ) − y i ) (y_i^{(s−1)}-y_i) (yi(s−1)−yi) (yi(s−1)−yi)(yi(s−1)−yi) 相同。被增强的完整训练数据可以这样定义:从均匀的原始数据中采样一个样本和一个关节,然后根据从 N i ( s − 1 ) \mathcal N_i^{(s-1)} Ni(s−1) 的采样的位移 δ δ δ 生成模拟预测:
D A s = { ( N ( x ; b ) , N ( y i ; b ) ) ∣ ( x , y i ) ∼ D , δ ∼ N i ( s − 1 ) b = ( y i + δ , σ diam ( y ) ) } D_{A}^{s}=\quad\left\{\left(N(x ; b), N\left(\mathbf{y}_{i} ; b\right)\right) \mid\right. \\ \left(x, \mathbf{y}_{i}\right) \sim D, \delta \sim \mathcal{N}_{i}^{(s-1)} \\ \left.b=\left(\mathbf{y}_{i}+\delta, \sigma \operatorname{diam}(\mathbf{y})\right)\right\} \\ DAs={(N(x;b),N(yi;b))∣(x,yi)∼D,δ∼Ni(s−1)b=(yi+δ,σdiam(y))}
级联阶段的训练目标如 公式 4 所示,通过特别注意来为每个关节使用正确的标准化:
θ
s
=
arg
min
θ
∑
(
x
,
y
i
)
∈
D
A
s
∥
y
i
−
ψ
i
(
x
;
θ
)
∥
2
2
\theta_{s}=\arg \min _{\theta} \sum_{\left(x, \mathbf{y}_{i}\right) \in D_{A}^{s}}\left\|\mathbf{y}_{i}-\psi_{i}(x ; \theta)\right\|_{2}^{2}
θs=argθmin(x,yi)∈DAs∑∥yi−ψi(x;θ)∥22
y i s ← y i ( s − 1 ) + N − 1 ( ψ i ( N ( x ; b ) ; θ s ) ; b ) ( 6 ) (3) \quad \mathbf{y}_{i}^{s} \leftarrow \mathbf{y}_{i}^{(s-1)}+N^{-1}\left(\psi_{i}\left(N(x ; b) ; \theta_{s}\right) ; b\right)(6) \tag{3} yis←yi(s−1)+N−1(ψi(N(x;b);θs);b)(6)(3)
Empirical Evaluation
试验评估部分介绍了作者的实验结果,不逐句翻译了,挑重点说。
数据集:
- Frames Labeled In Cinema: 包括来自好莱坞流行电影的 4000 个训练图像和 1000 个测试图像,每个人标记了 10 个上身关节。
- Leeds Sports Dataset: 包含 11000 个训练图像和 1000 个测试图像,来自体育活动,大多数只有 150 像素高度,每个人全身总共标记有 14 个关节。
作者将姿态 y 的直径定义直径定义为肩部和臀部之间的距离,并用 d i a m ( y ) diam(y) diam(y)表示。所有数据集的关节都排列在模仿人体的树中。这样就将肢体定义为姿态树中的一对相邻关节。
实验细节 :先对每个数据集使用一组 50 个的小图像来确定算法超参数。为了测量参数的最优性,所使用 PDJ 的平均值为超过所有关节的 0.2。缩放器 σ 被定义为精化关节边界框的大小,作为姿态大小的一部分:对于 FLIC选择 σ = 1.0 ,对于 LSP 作者使用 σ = 2.0 σ=2.0 σ=2.0。级联级数 S 由训练阶段确定,直到算法停止改进为止。对于 FLIC 和 LSP,令 S = 3。
为了改进泛化,对于从 s=2 开始的每个级联阶段,作者通过对每个关节抽样 40 个随机变换过的裁剪框来增加训练数据,如 3.2 节 中所述。因此,对于具有 14 个关节的 LSP 并且在对镜像进行镜像并对数量进行采样后,训练样本数目为 11000×40×2×14=12M,这对于训练大型网络是必要的。
结果与讨论
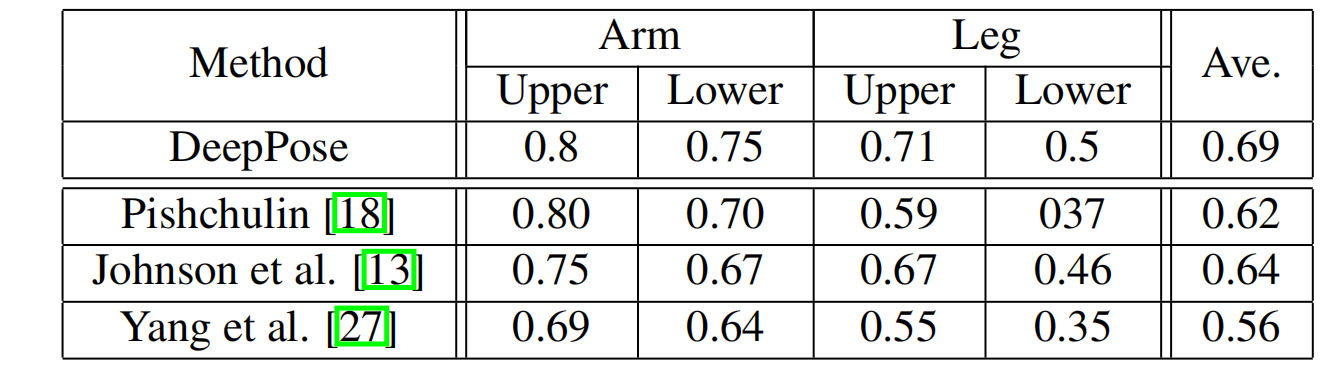
表 1 用于 Deep-Pose 的 LSP 上的正确部分(PCP)的百分比为 0.5,以及与五种最先进的方法的比较。作者使用稍微宽松的 PCP 版本,用每个肢体的平均值与预测肢体关节的距离用于确定是否正确检测到肢体。作者使用以人为中心的表示。

图 6 三级级联网络红色为预测姿态,绿色为ground truth。
5. Conclusion
作者提出了深度神经网络(DNN)在人体姿态估计中的首次应用,将问题表述为基于 DNN 的回归到关节坐标。所呈现的这种回归的级联具有以整体方式捕获关于姿态的背景和推理的优点。因此,作者能够在几个具有挑战性的学术数据集上实现最先进或更好的结果。
此外,作者展示了使用通用卷积神经网络的方法,该网络最初是为分类设计的任务,可以应用于不同的本地化任务。将来,作者计划研究新颖的架构,这些架构可能更适合一般的定位问题,尤其是姿态估计。