二叉搜索树

二叉搜索树（BST，Binary Search Tree）又称为二叉排序树，空树也算

二叉搜索树有如下性质

• 若左子树不为空，则左子树上所有节点值小于根节点
• 若右子树不为空，则右子树上所有节点值大于根节点
• 左子树和右子树也都是二叉搜索树

例如

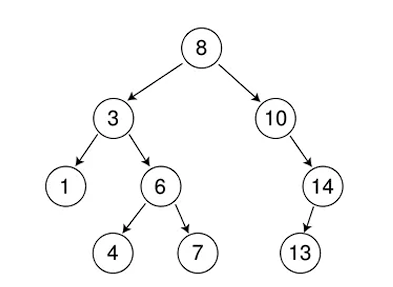
当然如果左大右小也可以

二叉搜索树的一个性质是中序遍历有序

查找

从根节点开始查找比较，比根大向右查找，比根小向左查找

最多查找高度次，如果没找到就代表值不存在

插入

如果为空，新增节点

如果不为空，按照性质插入节点

删除

首先需要确定值是否在二叉树中

要删除就右四种情况

1. 无子节点——直接删除即可，可以合并到只有一个节点的情况
2. 只有左节点——删除，令该节点的父节点指向左节点
3. 只有右节点——删除，令该节点的父节点指向右节点
4. 有两个子节点——在左子树寻找关键之最大的节点或右子树的最小节点，以最小节点为例，找到最小节点后与删除节点替换，再处理替换后的节点删除问题

实现

#pragma once
#include<iostream>

using namespace std;

template<class K> 
struct BSTreeNode // 二叉树节点，K表示关键字
{
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;

	BSTreeNode(cosnt K& key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{}
};

template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node;
public:
	// C++11
	BSTree() = default; // 强制生成默认构造

	~BSTree()
	{
		Destroy(_root);
	}

	BSTree(const BSTreeNode<K>& t)
	{
		_root = Copy(t._root);
	}

	BSTree<K>& operator=(BSTree<k> t)
	{
		swap(_root, t._root);
		return *this;
	}

	bool Insert(const K& key) // 建树，插入
	{
		if (_root == nullptr) // 空树
		{
			_root = new Node(key);
			return tree;
		}

		Node* parent = nullptr;
		Node* cur = _root;

		while (cur) // 找位置
		{
			parent = cur;
			if (cur->_key < key)
				cur = cur->_left; // 插入值比当前值小，进左树
			else if (cur->_key > key)
				cur = cur->_right; // 插入值比当前值大，进右树
			else
				return false; // 不允许出现重复值
		}

		cur = new Node(key);
		if (parent->_key < key) // 连接父节点
			parent->_right = cur;
		else
			parent->_left = cur;
	}

	bool Find(const K& key) 
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
				cur = cur->_right;
			else if (cur->_key > key)
				cur = cur->_left;
			else
				return true;  
		}
		return false;
	}

	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else // 找到了，准备删除
			{
				if (cur->_left == nullptr) // 左子树为空
				{
					// 当删除节点为根节点时，直接让根节点变为右子树即可
					if (cur == _root)
					{
						_root = cur->_right;
					}
					// 当删除节点不是根节点时，需要连接父节点和右子树
					else
					{
						// 判断当前节点是父节点的左孩子还是右孩子，确保正确连接
						if (cur == parent->_left)
						// 这里为什么不用防止parent是空指针呢
						// 因为只有根节点没有父节点，而前面一个判断已经把根节点单独处理过了
							parent->_left = cur->_right;
						else
							parent->_right = cur->_right;
					}
					delete cur;
				}
				else if (cur->_right == nullptr) // 右子树为空，与左子树为空类似
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left) 

							parent->_left = cur->_left;
						else
							parent->_right = cur->_left;
					}
					delete cur;
				}
				else // 左右都不为空
				{
					// 找到右子树的最小节点，替换后删除
					parent = cur; // 因为后面需要替换，防止出现解引用空指针
					Node* SubLeft = cur->_right; 
					// 表示右子树最小值，他一定在右子树的最高的最左边的那个节点上
					while (SubLeft->_left) // 找到该节点
					{
						parent = SubLeft;
						SubLeft = SubLeft->_left;
					}

					swap(cur->_key, SubLeft->_key); // 交换节点值

					// 最左节点一定是左子树为空，因此只需要父节点连接最左节点的右子树
					if (SubLeft == parent->_left) // 判断该节点是父节点的左节点还是右节点，再连接
						parent->_left = SubLeft->_right;
					else
						parent->_right = SubLeft->_right;
					delete SubLeft;
				}
				return true;
			}
			return false;
		}
	}

	void InOrder() // 中序遍历打印
	{
		// 中序遍历需要根节点，又不希望类外得到根节点
		// 这里可以只实现一个接口，内容是private即可
		// 后面的同理
		_InOrder(_root);
		cout << endl;
	}

	bool FindR(const K& key) // 递归查找
	{
		return _FindR(_root, key);
	}

	bool InsertR(const K& key)
	{
		return _InsertR(_root, K);
	}

	bool EraseR(const K& key)
	{
		return _EraseR(_root, key);
	}
private:
	Node* Copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;

		Node* newRoot = new Node(root->_key);
		newRoot->_left = Copy(root->_left);
		newRoot->_right = Copy(root->_right);

		return newRoot;
	}

	void Destroy(Node*& root)
	{
		if (root == nullptr)
			return;

		Destroy(root->_left);
		Destroy(root->_right);
		delete root;
		root = nullptr;
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
			return;

		_InOrder(root->_left);
		cout << root->_key << ' ';
		_InOrder(root->_right);
	}

	bool _FindR(Node* root, const K& key)
	{
		if (root == nullptr)
			return false;

		if (root->_key < key)
			return _FindR(root->_right, key);
		else if (root->_key > key)
			return _FindR(root->_left, key);
		else
			return true;
	}

	bool _InsertR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			// 这里的根节点是父节点左子树或者右子树的引用
			// 因此直接赋值就能连接
			root = new Node(key);
			return true;
		}

		if (root->_key < key)
			return _InsertR(root->_right, key);
		else if (root->_key > key)
			return _InsertR(root->_left, key);
		else
			return false;
	}

	bool _EraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
			return false;

		if (root->_key < key)
			return _EraseR(root->_right, key);
		else if (root->_key > key)
			return _EraseR(root->_left, key);
		else
		{
			if (root->_left == nullptr)
			{
				Node* del = root;
				root = root->_right; // root也是父节点左右子树的别名，因此直接赋值
				delete del;

				return true;
			}
			else if (root->_right == nullptr)
			{
				Node* del = root;
				root = root->_left;
				delete del;

				return true;
			}
			else
			{
				Node* SubLeft = root->_right;
				while (SubLeft->_left)
					SubLeft = SubLeft->_left;
				
				swap(root->_key, SubLeft->_key);

				// 替换之后，转换成在右子树递归删除即可
				return _EraseR(root->_right, key);
			}
		}
	}

	Node* _root = nullptr;
};

应用

二叉搜索树一般有两个应用

第一类是K模型，结构中只需要存储Key即可，关键之就是所需要的值，一般用于检测某个值是否存在

第二类是KV模型，结构中是<Key,Value>键值对，类似于字典

性能分析

插入和删除都必须先查找

插入的次序不同，会影响到二叉树的结构

最优情况下，二叉树为完全二叉树，其平均比较次数为${\log }_{2}N$

最差情况下，二叉树为单支树，其平均比较次数为$\frac{N}{2}$

因此当二叉树为单支树，我们应当如何改进，使其性能都达到最优，就需要引入AVL树和红黑树，这些我们在后面也会陆续讲解和实现