JD：

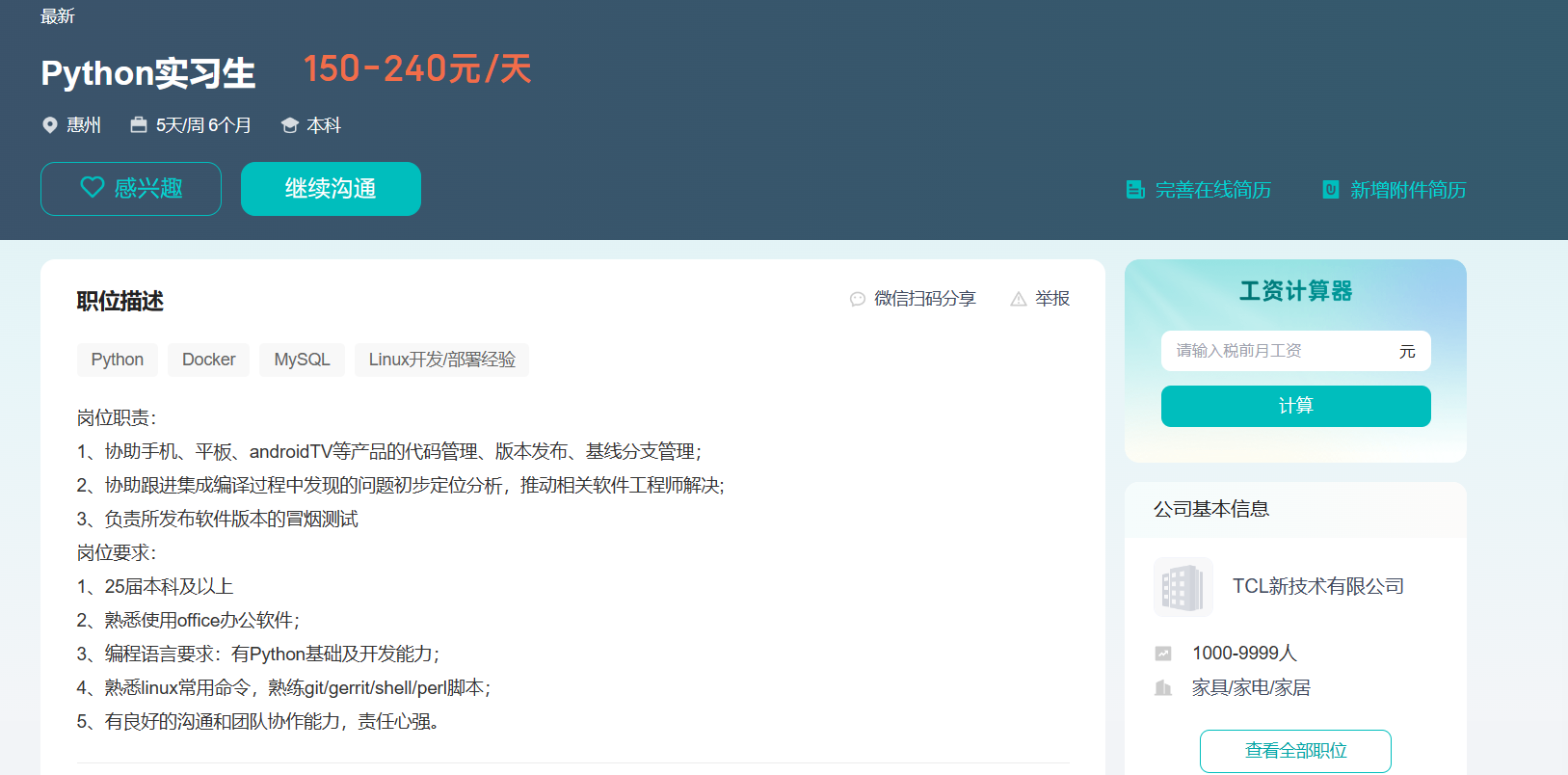
招聘流程：

2024.1.3 Boss直聘 沟通

2024.1.4 约面

2024.1.6 上午面试

面试流程：

上来第一步，直接问Python基础语法，讲一下基础的数据类型

就记得元组和字典

分别具体说一下元组和字典

流程控制语句有哪些？

for循环具体讲讲

Python库有用过哪些？具体说说

爬虫，可视化，词云图（这部分回答的不是很全面）

Linux有用过吗？

分布式，大数据开发

git有用过吗，主要做哪方面？

可以讲一下项目经历吗？

你在项目中承担哪些工作和任务呢？

就是会有写一些需求分析和项目背景是吧？

讲一下你在项目中遇到的挑战和成果？

有什么想反问的？

主要工作：工程效能部，集成开发，容器化

入职培训

你打算考研吗？

作为本地人您为什么会选择广东？

以前来过广东？

可以随时到岗是吗？