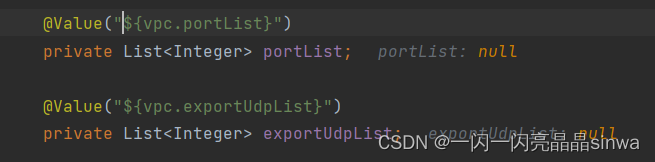
本次实验以AAAI 2014会议论文数据为基础,要求实现或调用无监督聚类算法,了解聚类方法。
任务介绍

每年国际上召开的大大小小学术会议不计其数,发表了非常多的论文。在计算机领域的一些大型学术会议上,一次就可以发表涉及各个方向的几百篇论文。按论文的主题、内容进行聚类,有助于人们高效地查找和获得所需要的论文。本案例数据来源于AAAI 2014上发表的约400篇文章,由UCI公开提供,提供包括标题、作者、关键词、摘要在内的信息,希望大家能根据这些信息,合理地构造特征向量来表示这些论文,并设计实现或调用聚类算法对论文进行聚类。最后也可以对聚类结果进行观察,看每一类都是什么样的论文,是否有一些主题。
基本要求:
-
将文本转化为向量,实现或调用无监督聚类算法,对论文聚类,例如10类(可使用已有工具包例如sklearn);
-
观察每一类中的论文,调整算法使结果较为合理;
-
无监督聚类没有标签,效果较难评价,因此没有硬性指标,跑通即可,主要让大家了解和感受聚类算法,比较简单。
扩展要求:
-
对文本向量进行降维,并将聚类结果可视化成散点图。
注:group和topic也不能完全算是标签,因为
-
有些文章作者投稿时可能会选择某个group/topic但实际和另外group/topic也相关甚至更相关;
-
一篇文章可能有多个group和topic,作为标签会出现有的文章同属多个类别,这里暂不考虑这样的聚类;
-
group和topic的取值很多,但聚类常常希望指定聚合成出例如5/10/20类;
-
感兴趣但同学可以思考利用group和topic信息来量化评价无监督聚类结果,不作要求。
提示:
-
高维向量的降维旨在去除一些高相关性的特征维度,保留最有用的信息,用更低维的向量表示高维数据,常用的方法有PCA和t-SNE等;
-
降维与聚类是两件不同的事情,聚类实际上在降维前的高维向量和降维后的低维向量上都可以进行,结果也可能截然不同;
-
高维向量做聚类,降维可视化后若有同一类的点不在一起,是正常的。在高维空间中它们可能是在一起的,降维后损失了一些信息
实验结果
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.metrics import calinski_harabasz_score
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import pandas as pd
import numpy as np
def load_data(path='data/[UCI] AAAI-14 Accepted Papers - Papers.csv'):
df_data = pd.read_csv(path)
df_data = df_data.dropna()
return df_data
df = load_data()
df.describe() # 去除不好的特征
df_selected = df.drop(['groups', 'topics'], axis=1)
cv = CountVectorizer()
X_features = np.array([[i] for i in range(df.shape[0])])
for col in df_selected.columns:
tmp = cv.fit_transform(df_selected[col].tolist())
feature = tmp.toarray()
X_features = np.concatenate((X_features, feature), axis=1)
print("特征矩阵的形状:", X_features.shape)
特征矩阵的形状: (392, 9899)
# 取出group和topics特征作为评价指标
df_cls = df[['groups', 'topics']]
cv = CountVectorizer()
X_cls = [[i] for i in range(df.shape[0])]
for col in df_cls.columns:
tmp = cv.fit_transform(df_cls[col])
feature = tmp.toarray()
X_cls = np.concatenate((X_cls, feature), axis=1)
SSE(Sum of Squared Errors)测量聚类结果中每个样品与所属聚类中心距离的平方和。SSE越小,聚类样品越致密,聚类效果越好。SSE是衡量簇内密度的指标,越小越好。
CH指标(Calinski-HarabaszIndex)是综合考虑集群内密度和集群间分辨率的指标。计算集群间分散度与集群内密度之比。CH指标越大,集群之间的距离越大,集群内的距离越小,集群效果越好。
for pca_num in [2, 5, 7, 10, 30]:
X_pca = PCA(n_components=pca_num).fit_transform(X_features)
X_cs = PCA(n_components=pca_num).fit_transform(X_cls)
print(X_pca.shape)
for k in range(5, 16):
kmeans = KMeans(n_clusters=k)
labels = kmeans.fit_predict(X_pca)
# 获取聚类中心
centroids = kmeans.cluster_centers_
# 计算每个样本与所属簇中心的距离的平方
distances = np.sum((X_cs - centroids[labels])**2, axis=1)
# 计算 SSE
sse = np.sum(distances)
# CH指标
ch = calinski_harabasz_score(X_cs, labels)
score = sse/ch
print('k:', k, 'ch:', ch, 'SSE:', sse, 'score:', score)

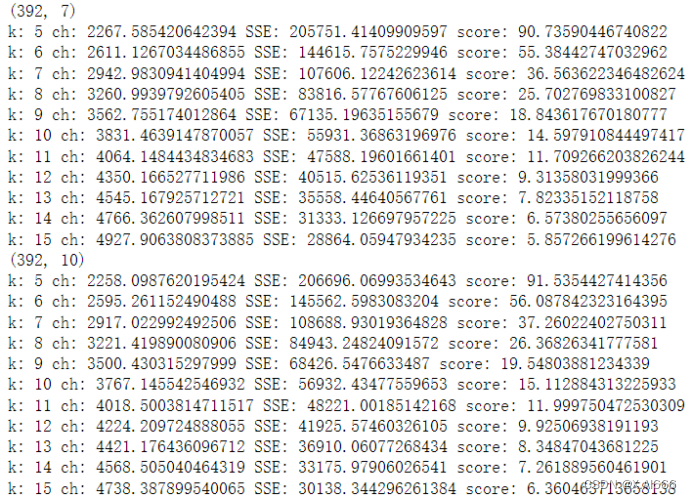
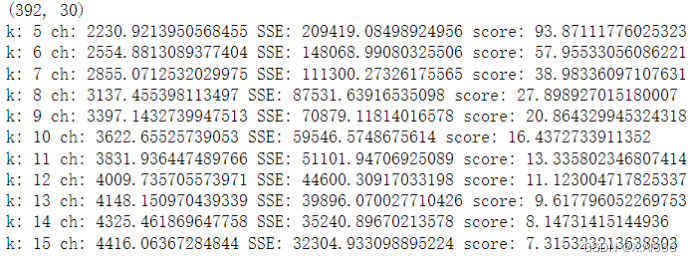
从结果可以看出降维度在2,k为15的时候聚类效果更好。这里我用了sse和ch的比值作为成绩,越小证明聚类效果越好。