看了李煜东老师的答案。
对dp的转移有了一点别的理解。
之前都是按y总那样考虑当前状态是由那些状态转移过来的。
这道题目看算阶上的思考方式，考虑的是当前状态能够转移到那些状态。
更具体点就是说，考虑$f[i][j][k][l][r]$我可以把这一个人放在哪一行。
$f[i+1][j][k][l][r]$就是把这个人放在第一行。
也就是$f[i][j][k][l][r]$可能能转移到$f[i+1][j][k][l][r]$
但是转移是需要满足条件的
也就是满足按行递增、按列递增
考虑从1~n去放，第一行一定能放这是没有问题的。
也就是第一行只需要满足$i<a[1]$就可以放
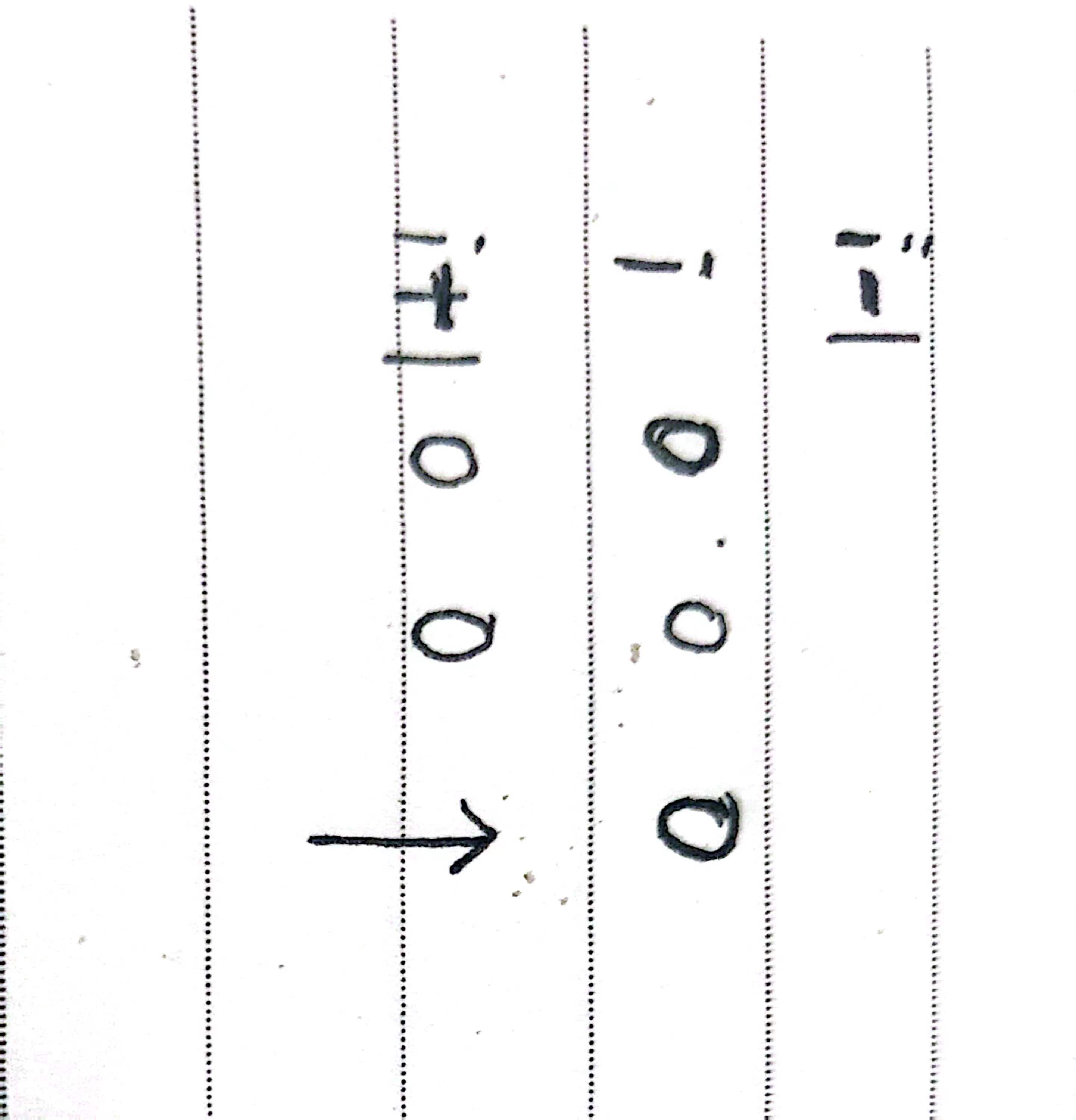
其他的行需要额外满足按列递增也就是要放的这一行的这一列它的上一行之前一定已经放过数了。也就是如下图，只有前面放过数了才能保证按列是递增的，行就没有这个问题，因为行本身就能保证这个性质。
总结：真的是很不错的dp题目，第一道就给了我一个下马威。

1. dp题要算一下空间可能会爆空间。
2. 多测，清数组要清干净。不然wa到自闭。
   

#include <bits/stdc++.h>

#define int long long
#define rep(i, a, b) for(int i = (a); i <= (b); ++i)
#define fep(i, a, b) for(int i = (a); i >= (b); --i)
#define _for(i, a, b) for(int i=(a); i<(b); ++i)
#define pii pair<int, int>
#define pdd pair<double,double>
#define ll long long
#define db double
#define endl '\n'
#define fs first
#define sc second
#define pb push_back
#define vi vector<int>

using namespace std;
const int maxn = 2e5 + 10;
int n;
int a[10];

void solve()
{

    while (cin >> n && n)
    {
        memset(a,0,sizeof(a));
        rep(i, 1, n)
        {
            cin >> a[i];
        }

        int f[a[1]+3][a[2]+3][a[3]+3][a[4]+3][a[5]+3];
        memset(f,0,sizeof(f));
        f[0][0][0][0][0] = 1;
        rep(i, 0, a[1])
        {
            rep(j, 0, a[2])
            {
                rep(k, 0, a[3])
                {
                    rep(l, 0, a[4])
                    {
                        rep(r, 0, a[5])
                        {
                            if (i < a[1])
                            {
                                f[i + 1][j][k][l][r] += f[i][j][k][l][r];
                            }
                            if (i > j)
                            {
                                f[i][j + 1][k][l][r] += f[i][j][k][l][r];
                            }
                            if (j > k)
                            {
                                f[i][j][k + 1][l][r] += f[i][j][k][l][r];
                            }
                            if (k > l)
                            {
                                f[i][j][k][l + 1][r] += f[i][j][k][l][r];
                            }
                            if (l > r)
                            {
                                f[i][j][k][l][r + 1] += f[i][j][k][l][r];
                            }
                        }
                    }
                }
            }
        }
        int ans = f[a[1]][a[2]][a[3]][a[4]][a[5]];
        cout << ans << '\n';
    }

}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
//    freopen("C:\\Users\\24283\\CLionProjects\\untitled2\\1.in", "r", stdin);
    solve();
    return 0;
}