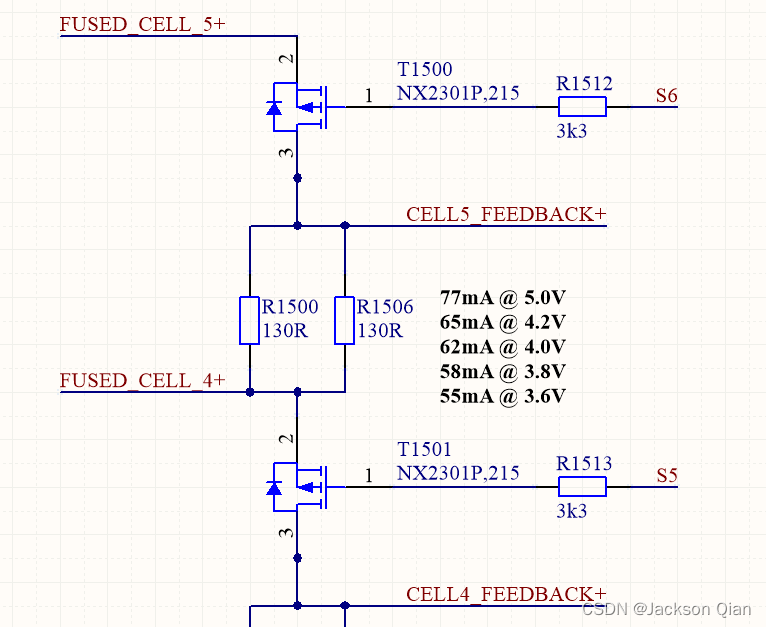
1、LT6813采用内部均衡的原理
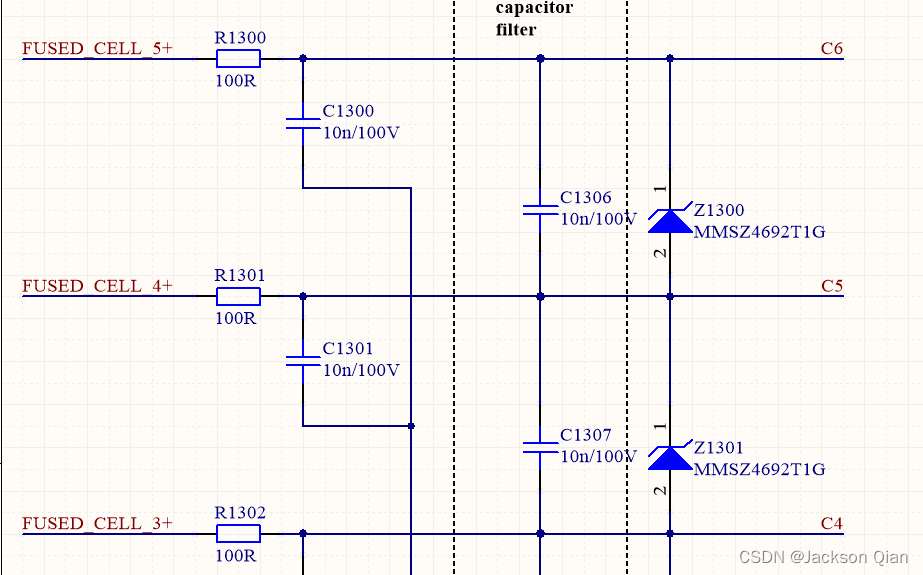
2、平衡控制结构体
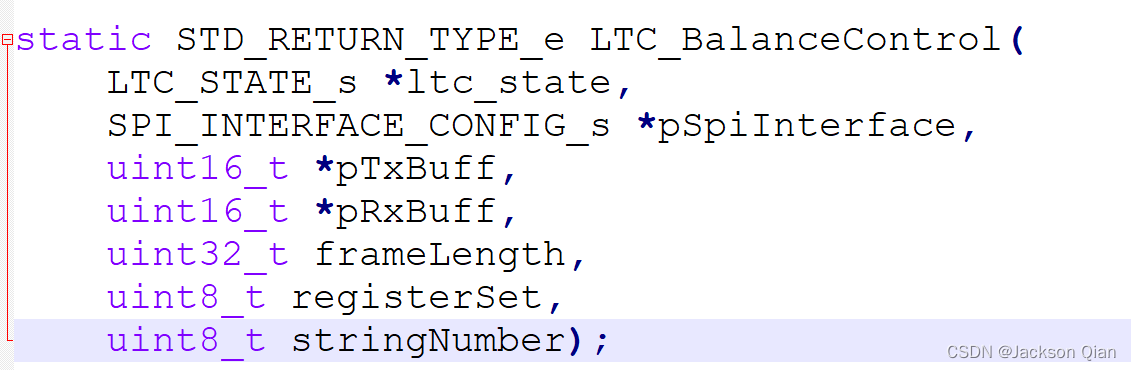
根据数据库中读取的控制值设置平衡。要为单元设置平衡,必须将相应的位写入配置寄存器中。LTC 驱动程序仅执行数据库中 BMS 写入的数据。
参数
| ltc_state | LTC 状态机的状态 |
| pSpi接口 | 指向 SPI 配置的指针 |
| pTxBuff (英语) | 传输缓冲区 |
| pRxBuff | 接收缓冲区 |
| 帧长度 | 要传输的字数 |
| registerSet | 寄存器集,0:单元格 1 至 12 (WRCFG),1:单元格 13 至 15/18 (WRCFG2) |
| 字符串编号 | 已寻址的字符串 |
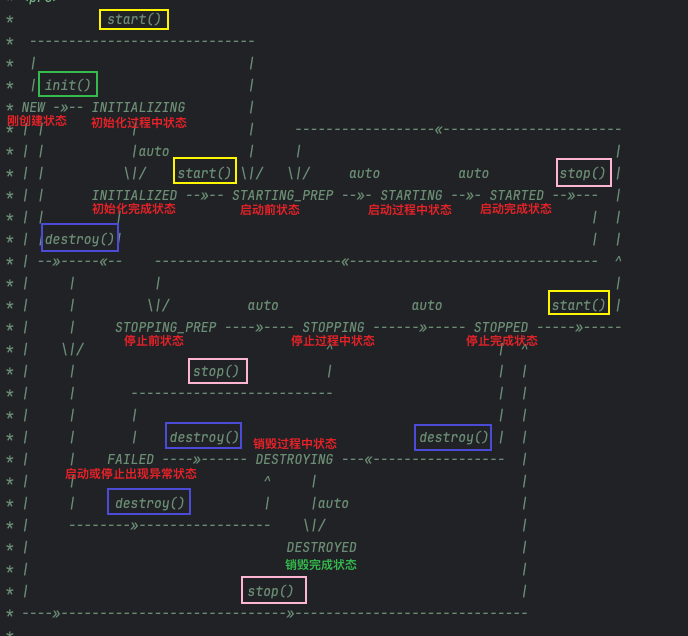
状态机转换

基于条件的状态转换,取决于 retVal。如果 retVal STD_OK,则在经过timer_ms_ok后,LTC 状态机将转换为 state_ok 和 substate_ok,否则在 timer_ms_nok 后,状态机将转换为 state_nok 和 substate_nok。根据 retVal 的值,将调用相应的诊断条目。
参数
| ltc_state | LTC 状态机的状态 |
| retVal | 条件,以确定状态机是转换为 OK 还是 NOK 状态 |
| diag代码 | 用于诊断输入的符号 ID,如果 retVal STD_OK,则用 DIAG_EVENT_OK 调用,否则DIAG_EVENT_NOT_OK DIAG_EVENT_NOT_OK |
| state_ok | 如果 retVal 为 STD_OK,则要转换为状态 |
| substate_ok | 如果 retVal 为 STD_OK,则转换为子状态 |
| timer_ms_ok | 过渡到state_ok,substate_ok timer_ms_ok过后 |
| state_nok | 如果 retVal 为 STD_NOT_OK,则要转换为状态 |
| substate_nok | 如果 retVal STD_NOT_OK,则要转换为子状态 |
| timer_ms_nok | 过渡到state_nok,timer_ms_nok过后substate_nok |
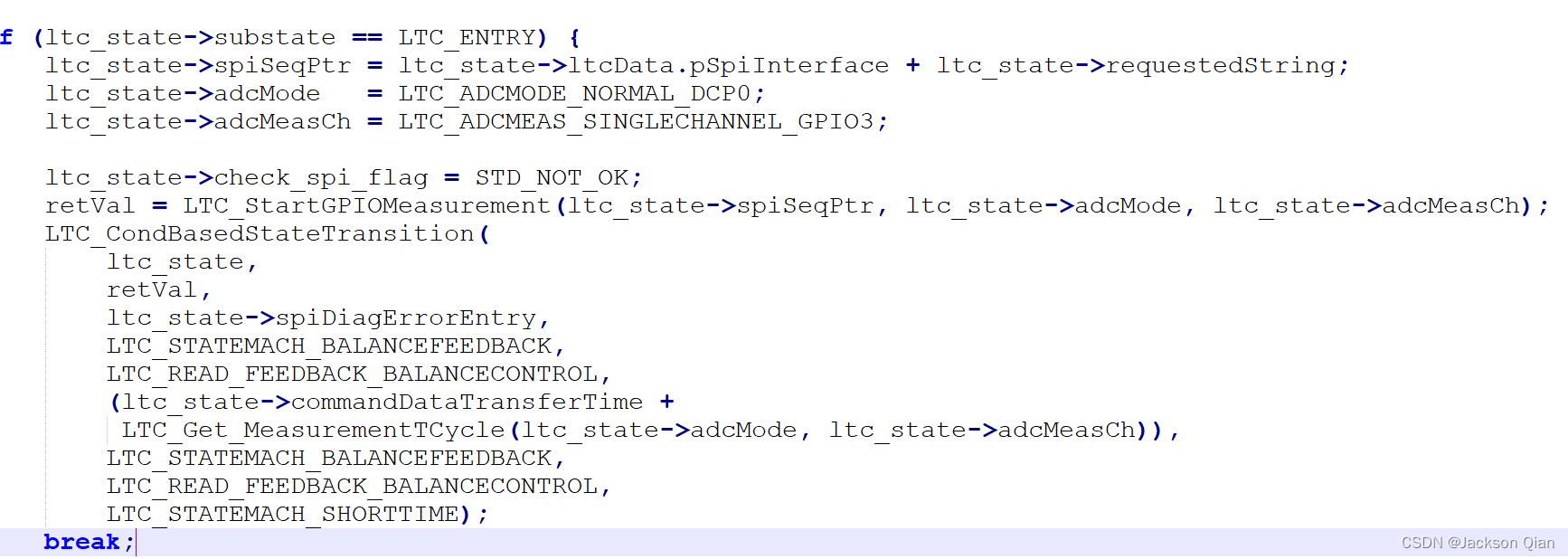
3、均衡控制逻辑
程序通过ltc_state->substate 的状态做轮询处理

获取retVal的当前状态值

均衡前确保AFE不是处于电压采样模式

12串以上的电芯均衡

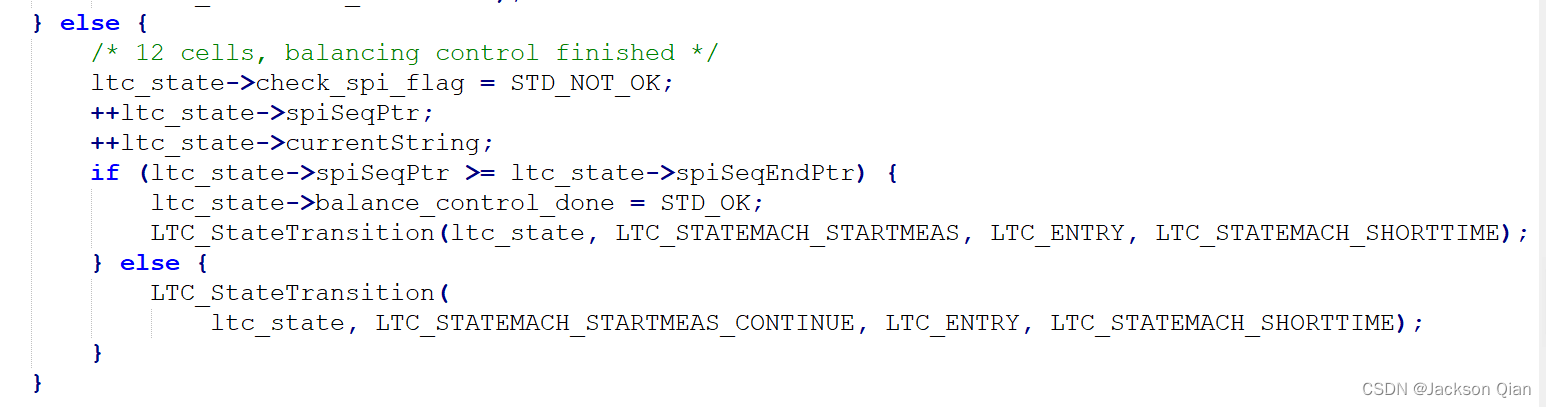
均衡结束
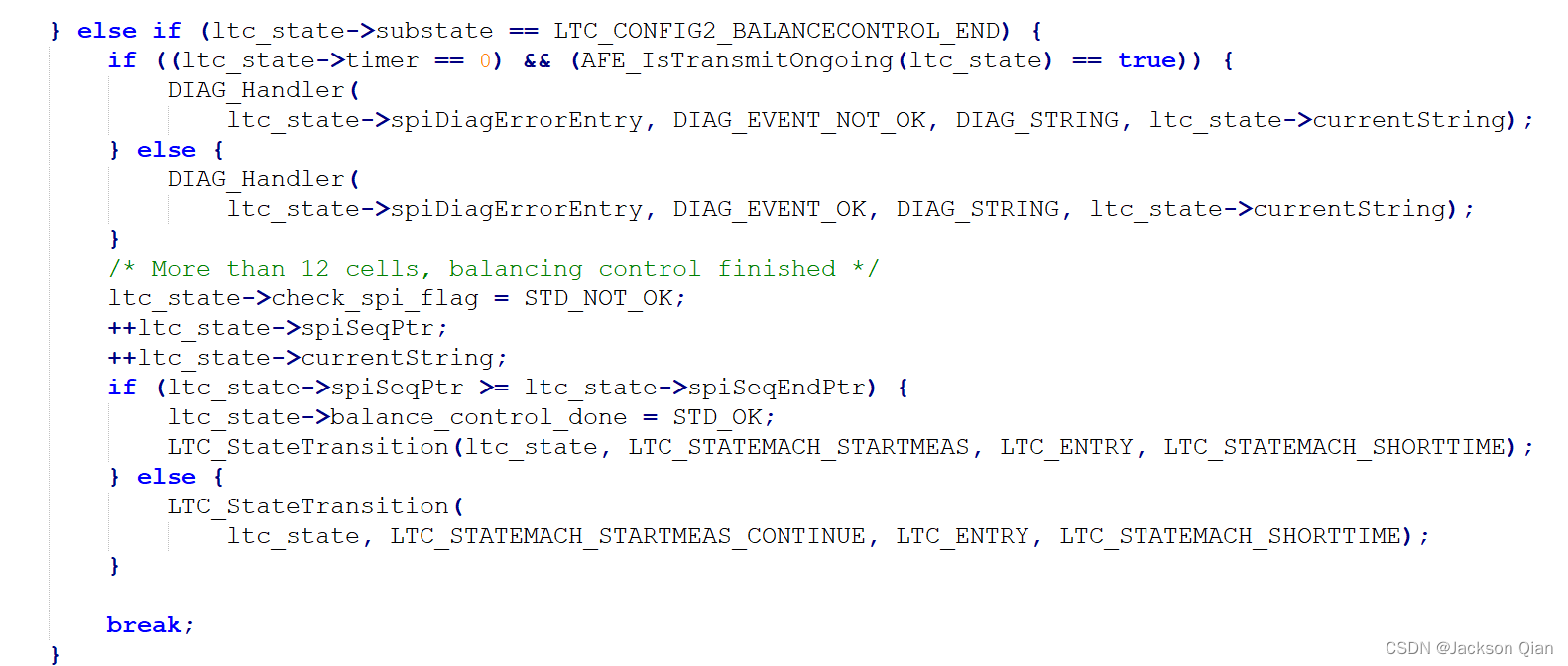
4、均衡状态反馈
将测得的平衡反馈值存储在数据库中。此函数将在 LTC 的 GPIO3 上测量的全局平衡反馈值存储到数据库中