栈和队列OJ题：有效的括号，用栈实现队列，用队列实现栈，设计循环队列（C语言版，图文并茂，超级详细）

前言

1. 有效的括号

（1）题目及示例

（2）思路及解法

2.用栈实现队列

（1）题目及示例

（2）解析及思路

（3）各部分代码

2.3.1 数据结构设计和创造队列

2.3.2 入队列出队列

2.3.3 获取队列开头元素判空销毁队列

3.用队列实现栈

（1）题目及示例

（2）解析及思路

（3）完整代码

3.3.1 队列实现代码

3.3.2 数据结构的设计和创造栈

3.3.3 入栈出栈

3.3.4 获取栈顶元素判空销毁栈

4.设计循环队列

（1）题目及示例

（2）解析及思路

4.2.1 链表思路

4.2.2 数组实现（重点）

（3）各部分代码

4.3.1数据结构的设计和创造队列

4.3.2 入队列出队列

4.3.3 获取队头和队尾的数据

4.3.4 判空判满销毁队列

总结

前言

这篇文章将带来栈和队列四道经典的OJ题目，每道题都有图示加上文字分析，，让你理解起来更加简单，题目后面有Leetcode做题链接，话不多说，来看看吧！

1. 有效的括号

（1）题目及示例

给定一个只包括 '('，')'， '{'，'}'， '['，']' 的字符串 s ，判断字符串是否有效。有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

Leetcode链接：. - 力扣（LeetCode）

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 1：

输入：s = "(]"
输出：false

（2）思路及解法

这道题有三对左括号和右括号，是互相匹配的。出现示例2()[]{}和{ [ ( [ ] ) ] }这两种情况都是匹配的，我们可以创建一个栈，遇到左括号就入栈，遇到右括号就出栈，然后再对比是否匹配，不匹配就返回false，然后继续识别。

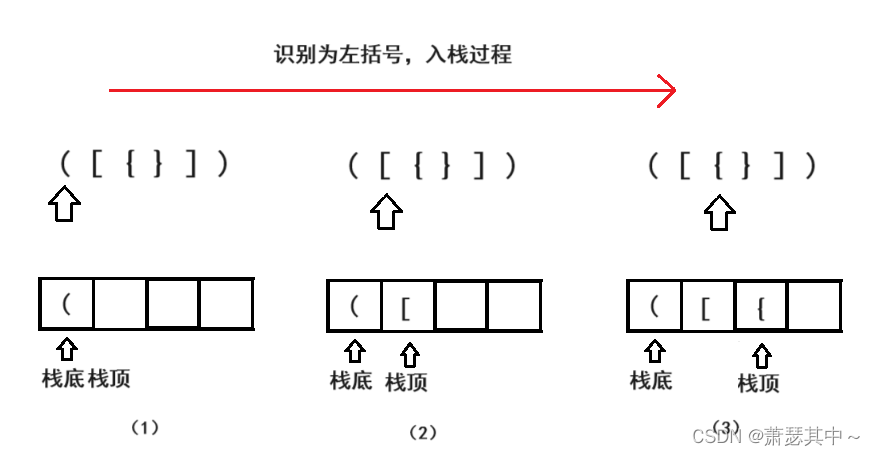
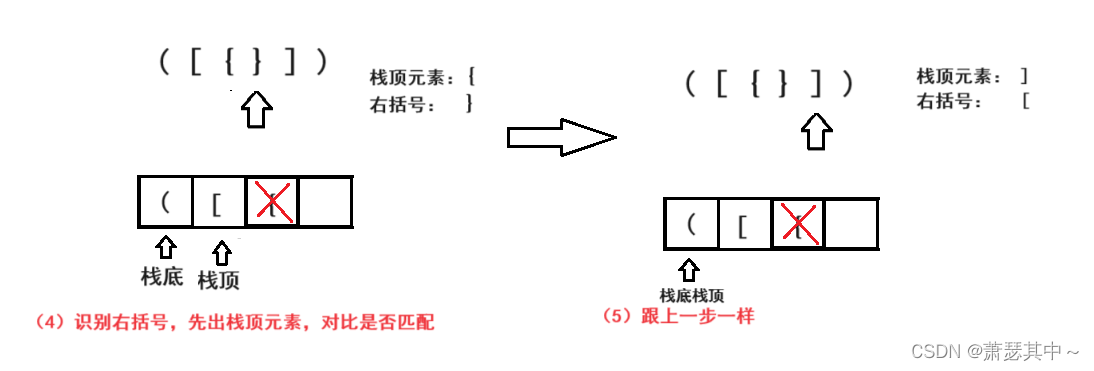
所以我们需要建立一个栈，刚好上一篇文章就是栈和队列http://t.csdnimg.cn/ECRaS。不过第一行的数据类型需要改成char。

typedef char STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;

void StackInit(ST* ps);
void StackDestroy(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPop(ST* ps);
STDataType StackTop(ST* ps);
int StackSize(ST* ps);
bool StackEmpty(ST* ps);

void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;//ps->top = -1
	ps->capacity = 0;
}


void StackDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}


void StackPush(ST* ps, STDataType x)
{
	assert(ps);

	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = realloc(ps->a, sizeof(STDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}

		ps->a = tmp;
		ps->capacity = newCapacity;
	}

	ps->a[ps->top] = x;
	ps->top++;
}


void StackPop(ST* ps)
{
	assert(ps);
	//assert(ps->top > 0);
	assert(!StackEmpty(ps));

	ps->top--;
}

STDataType StackTop(ST* ps)
{
	assert(ps);
	//assert(ps->top > 0);
	assert(!StackEmpty(ps));

	return ps->a[ps->top - 1];
}

int StackSize(ST* ps)
{
	assert(ps);

	return ps->top;
}


bool StackEmpty(ST* ps)
{
	assert(ps);

	return ps->top == 0;
}

然后就是解决问题的代码。

bool isValid(char* s) 
{
    ST st;
    StackInit(&st);
    while(*s)
    {
        if (*s == '(' 
        || *s == '{' 
        || *s == '[')
        {
            StackPush(&st, *s);
        }
        else
        {
            //遇到右括号了，但是栈里面没有数据
            //说明前面没有左括号，不匹配
            if (StackEmpty(&st))
            {
                StackDestroy(&st);
                return false;
            }

            STDataType top = StackTop(&st);
            StackPop(&st);
            if ((*s == '}' && top != '{')
            || (*s == ']' && top != '[')
            || (*s == ')' && top != '('))
            {
                StackDestroy(&st);
                return false;
            }
        }
        ++s;
    }

    //如果栈不是空，说有栈中还有左括号未出
    bool ret = StackEmpty(&st);
    StackDestroy(&st);
    return ret;
}

2.用栈实现队列

（1）题目及示例

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空，返回 true ；否则，返回 false

Leetcode链接：. - 力扣（LeetCode）

说明：

你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"] 
[[], [1], [2], [], [], []] 输出： [null, null, null, 1, 1, false] 
解释： 
MyQueue myQueue = new MyQueue(); 
myQueue.push(1); // queue is: [1] 
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false

（2）解析及思路

这道题让我们使用两个栈来模拟实现一个队列。因为我们是用C语言来实现，所以栈的实现直接复制上一篇文章中的代码，详情可看http://t.csdnimg.cn/ivgOe《栈和队列实现》。

我们先画图分析，先在第一个栈入栈1,2,3,4这四个数据。

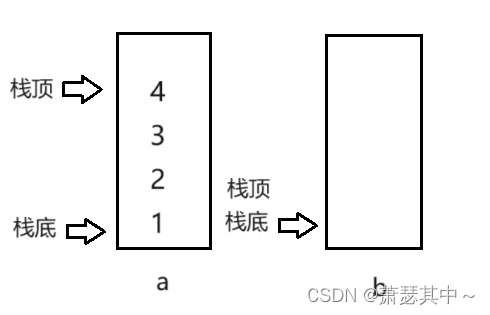
栈是后进先出，队列是先进先出。当我们要出数据的时，怎么样才能做到队列的先进先出呢？我们要得到数据1，但是栈会先出数据4，所以我们可以先将数据出到第二个栈上，如下图。
然后利用栈的基础接口函数获取栈顶元素(StackTop)，然后再出数据1。
那之后再要出数据该怎么办呢？

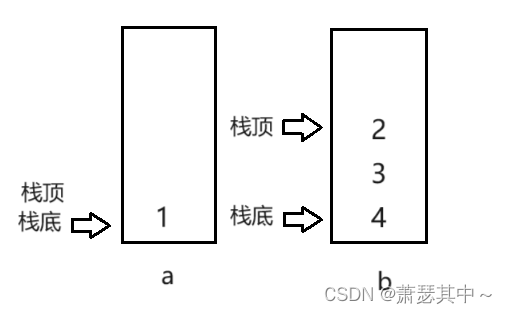
我们观察栈b，发现它出数据的顺序是2,3,4，这就符合队列的先进先出。
之后再入数据该放哪呢？可以放在栈a上，比如数据5,6,7,8，如下图。

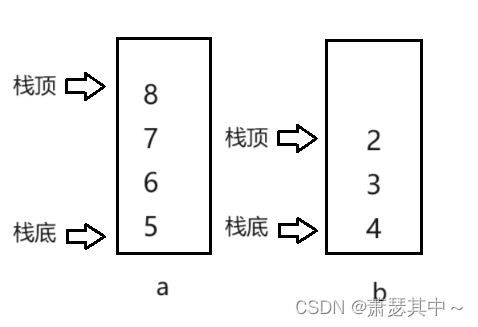
所以我们可以让栈a专门来入数据，栈b专门来出数据，不过第一次的出数据的时候，需要把数据倒过来，然后再获取栈顶元素。我们命名栈a为pushST，栈b为popST。

这里先放栈的接口函数：

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;

void StackInit(ST* ps);
void StackDestroy(ST* ps);
void StackPush(ST* ps, STDataType x);
void StackPop(ST* ps);
STDataType StackTop(ST* ps);
int StackSize(ST* ps);
bool StackEmpty(ST* ps);

void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;//ps->top = -1
	ps->capacity = 0;
}

void StackDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}

void StackPush(ST* ps, STDataType x)
{
	assert(ps);

	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = realloc(ps->a, sizeof(STDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}

		ps->a = tmp;
		ps->capacity = newCapacity;
	}

	ps->a[ps->top] = x;
	ps->top++;
}

void StackPop(ST* ps)
{
	assert(ps);
	//assert(ps->top > 0);
	assert(!StackEmpty(ps));

	ps->top--;
}

STDataType StackTop(ST* ps)
{
	assert(ps);
	//assert(ps->top > 0);
	assert(!StackEmpty(ps));

	return ps->a[ps->top - 1];
}

int StackSize(ST* ps)
{
	assert(ps);

	return ps->top;
}

bool StackEmpty(ST* ps)
{
	assert(ps);

	return ps->top == 0;
}

（3）各部分代码

2.3.1 数据结构设计和创造队列

定义两个栈一个来出数据，另外一个来入数据。并且这个结构体是个匿名结构体，可以重命名得到结构体名MyQueue。myQueueCreate函数先动态开辟一个MyQueue类型的指针变量，利用上面的接口函数初始化pushST和popST。这里需要注意的是&和->这两个符号的优先级，->优先级别更高所以是先用结构体指针q先指向pushST这个结构体中的变量，然后在取地址&，所以传入的是一个指针。

typedef struct {
    ST pushST;
    ST popST;
} MyQueue;

MyQueue* myQueueCreate() {
    MyQueue* q = (MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&q->pushST);
    StackInit(&q->popST);

    return q;
}

2.3.2 入队列出队列

入队列很简单，直接在栈pushST里面入数据即可，没有条件限制。

void myQueuePush(MyQueue* obj, int x) 
{
    StackPush(&obj->pushST, x);
}

出数据是要拿到一开始的数据，我们先判断栈popST是否为空，为空就把栈pushST的数据倒过去，这样popST里的数据就满足先进先出的顺序。if语句里面使用一个while循环，判断条件是pushST里不为空，就用栈的接口函数将栈顶元素入到popST中，然后pushST中出数据。

int myQueuePop(MyQueue* obj) {
    //如果popST中没有数据，讲pushST的数据导过去
    //popST中的数据就符合先进先出的顺序了
    if (StackEmpty(&obj->popST))
    {
        while(!StackEmpty(&obj->pushST))
        {
            StackPush(&obj->popST, StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }
    }

    int front = StackTop(&obj->popST);
    StackPop(&obj->popST);
    return front;
}

2.3.3 获取队列开头元素判空销毁队列

获取队列开头元素，先用栈的判空判断popST中是否有元素，如果为空，需要将pushST中的元素倒过来，然后再进行操作。

int myQueuePeek(MyQueue* obj) {
     if (StackEmpty(&obj->popST))
    {
        while(!StackEmpty(&obj->pushST))
        {
            StackPush(&obj->popST, StackTop(&obj->pushST));
            StackPop(&obj->pushST);
        }
    }

    return StackTop(&obj->popST);
}

队列的判空可以直接返回对这两个栈的判空，如果都为空就会返回真，只要其中一个不为空，就返回false。
销毁栈，先调用栈的销毁函数，来销毁pushST和popST这两个栈，再释放obj动态开辟的空间。

bool myQueueEmpty(MyQueue* obj) {
    return StackEmpty(&obj->pushST) && StackEmpty(&obj->popST);
}

void myQueueFree(MyQueue* obj) {
    StackDestroy(&obj->pushST);
    StackDestroy(&obj->popST);
    free(obj);
}

3.用队列实现栈

（1）题目及示例

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

Leetcode链接：. - 力扣（LeetCode）

注意：

你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

（2）解析及思路

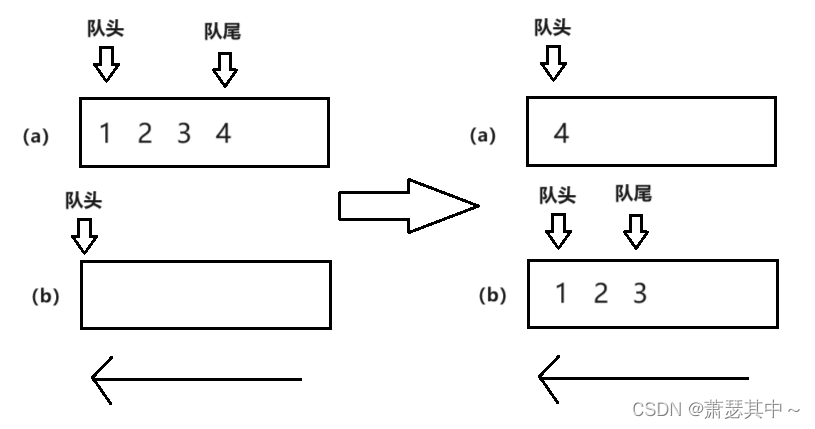
我们先画图表示两个队列，在队列a中入数据1，2，3，4，队列b的队头和队尾指向空。

栈是后进先出，而队列先进先出。也就是说，下面的队列是按照1234这个顺序出数据，我们要的是出数据时拿到4。
所以可以现将123这三个数据先出队列，放到队列b中，当队列a中只有一个数据4的时候，就出队列，拿到4。因此，我们需要一个队列保持空的状态，另一个有数据，当要出数据的时候，导到空队列中，再把出最后一个数据即可。

（3）完整代码

3.3.1 队列实现代码

队列实现代码，详情可看《栈和队列的实现C语言版》http://t.csdnimg.cn/IiLKj。

typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QueueNode;

typedef struct Queue
{
	QueueNode* head;
	QueueNode* tail;
}Queue;

void QueueInit(Queue* pq); 
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = NULL;
	pq->tail = NULL;
}

void QueueDestroy(Queue* pq)
{
	assert(pq);
	QueueNode* cur = pq->head;
	while (cur != NULL)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}

	pq->head = pq->tail = NULL;
}

void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	newnode->data = x;
	newnode->next = NULL;

	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}

void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	QueueNode* next = pq->head->next;
	free(pq->head);
	pq->head = next;
}

QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->head->data;
}

QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->tail->data;
}

int QueueSize(Queue* pq)
{
	assert(pq);

	int n = 0;
	QueueNode* cur = pq->head;
	while (cur)
	{
		n++;
		cur = cur->next;
	}

	return n;
}

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}

3.3.2 数据结构的设计和创造栈

我们的栈用两个队列q1和q2来实现，myStackCreate函数先动态开辟一个MyStack结构体指针，再使用队列的初始化接口函数，初始化两个队列。这里需要注意的是&和->这两个符号的优先级，->优先级别更高所以是先用结构体指针q先指向pushST这个结构体中的变量，然后在取地址&，所以传入的是一个指针。

typedef struct {
    Queue q1;
    Queue q2;
} MyStack;

MyStack* myStackCreate() {
    MyStack* st = (MyStack*)malloc(sizeof(MyStack));
    QueueInit(&st->q1);
    QueueInit(&st->q2);
    return st;
}

3.3.3 入栈出栈

入数据的时候我们要判断哪个队列不为空，不为空就在这个队列中入数据。

void myStackPush(MyStack* obj, int x) {
    if (!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1, x);
    }
    else
    {
        QueuePush(&obj->q2, x);
    }
}

出数据的时候，我们要判断哪个是空队列。我们可以先假设q1是空队列，q2不为空，然后判断q1是否为空，为空就交换emptyQ和noemptyQ指针指向的队列。然后让不为空的队列出数据，并放到空队列中，直到一开始不为空的队列元素个数为1，再获取这个元素，就完成了出数据

int myStackPop(MyStack* obj) {
    Queue* emptyQ = &obj->q1;
    Queue* nonemptyQ = &obj->q2;

    if (!QueueEmpty(&obj->q1))
    {
        emptyQ = &obj->q2;
        nonemptyQ = &obj->q1;
    }

    while(QueueSize(nonemptyQ) > 1)
    {
        QueuePush(emptyQ, QueueFront(nonemptyQ));
        QueuePop(nonemptyQ);
    }

    int top = QueueFront(nonemptyQ);
    QueuePop(nonemptyQ);
    return top;
}

3.3.4 获取栈顶元素判空销毁栈

获取栈顶元素先判断哪个队列不为空，然后调用队列的获取队尾元素的接口函数。
判空就直接返回这两个队列判空，只要其中一个队列为空就返回false，否则返回true。
销毁栈，直接调用队列的销毁函数，再释放obj这个结构体指针。

int myStackTop(MyStack* obj) {
    if (!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

4.设计循环队列

（1）题目及示例

设计你的循环队列实现。循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

MyCircularQueue(k): 构造器，设置队列长度为 k 。
Front: 从队首获取元素。如果队列为空，返回 -1 。
Rear: 获取队尾元素。如果队列为空，返回 -1 。
enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
isEmpty(): 检查循环队列是否为空。
isFull(): 检查循环队列是否已满。

Leetcode链接：. - 力扣（LeetCode）

示例：

MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1);  // 返回 true
circularQueue.enQueue(2);  // 返回 true
circularQueue.enQueue(3);  // 返回 true
circularQueue.enQueue(4);  // 返回 false，队列已满
circularQueue.Rear();  // 返回 3
circularQueue.isFull();  // 返回 true
circularQueue.deQueue();  // 返回 true
circularQueue.enQueue(4);  // 返回 true
circularQueue.Rear();  // 返回 4

（2）解析及思路

4.2.1 链表思路

本文的循环队列，固定空间大小，但是可以重复利用空间来存储数据。这道题更加推荐使用数组来实现，虽然链表也可以实现，但是操作起来比较麻烦。

我们先分析使用链表来设计循环队列，我们设置一个大小为4的循环队列，即链表结点个数为4。当链表为空时，我们让front指针和rear指针，同时指向一个结点。

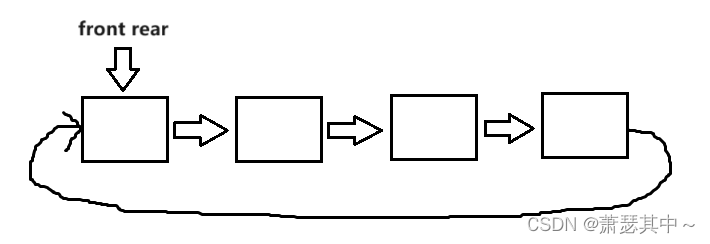
我们先入队列1,2,3，然后rear指针在每入一个数据的时候，指向下一个结点。这时刚好到最后一个空结点。

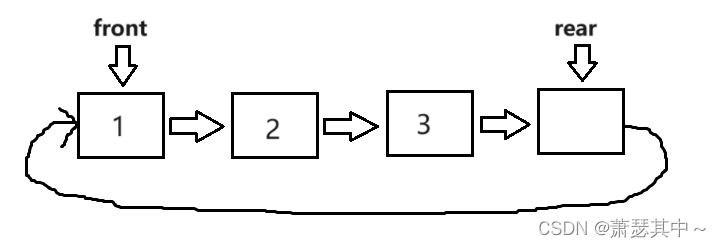
当我们再入一个数据4，会发现，rear指针和front指针指向同一个结点。这与我们刚开始判断链表为空的状态一样，这就无法判断当front指针和rear指针指向同一个结点时，到底是链表为空还是链表已经满了。

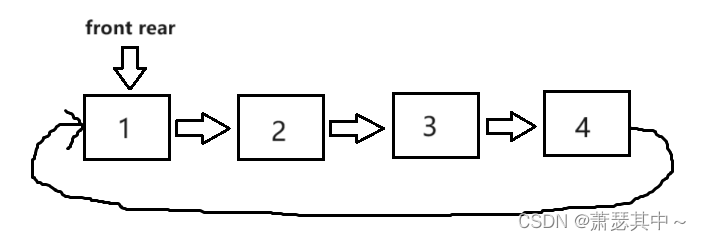
这时有些小伙伴就会想到创建一个size整型变量来计数，上面的链表为空和链表满了的情况，如下图所示。确实完美解决两指针指向同一个位置的问题。

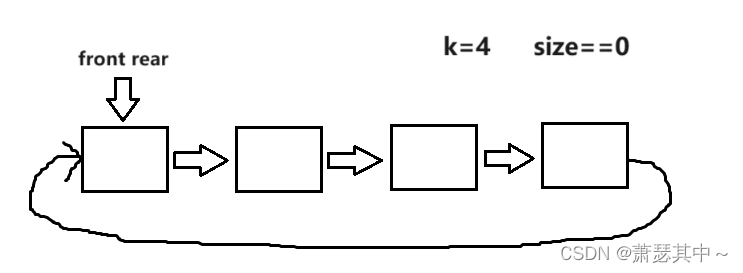
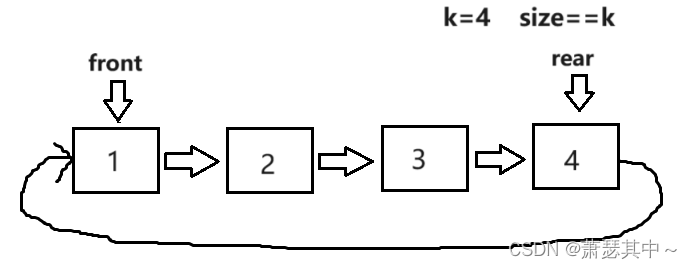
但是在上图中，如果我们要取到获取队尾的元素，不好获取。想要解决这个问题可以使用双向链表。

不过一开始初始化的时候，你还必须自己创建一个循环链表，比较麻烦。下面就介绍使用数组的方法，相对简单一些。

4.2.2 数组实现（重点）

一开始队列为空的时候，我们让front指针和rear指针的下标都赋值为0，不过当front与rear相等时，就表明队列为空。

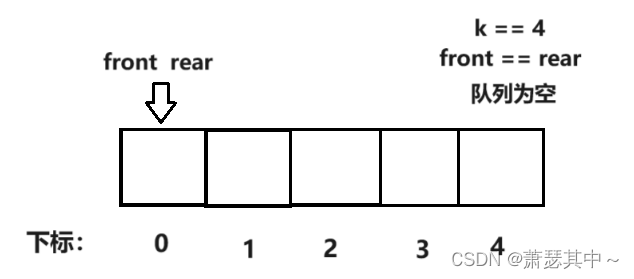
我们给循环队列入四个数据{1,2,3,4}，每入一个数据rear值加1，当入数据的个数为4的时候，rear赋值为最后一个数组下标。rear的值为那个空数组成员的下标，等于4。

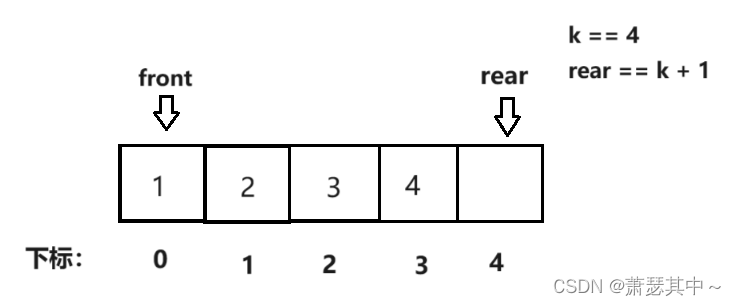
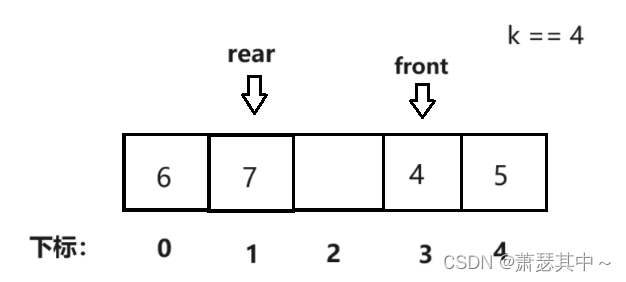
但是如果我们先出两个数据{1,2,3}，然后在入数据{5,6,7}。入数据的时候，rear在数组尾部，需要会到数组的开头，在这里可能很多小伙伴会在这里做特殊处理，但是会变得繁琐。
不做特殊处理，让rear取模，模上k+1。因为模上k+1，得到的余数范围是0~k，如rear=4时，入数据5时，rear需要加1，我们让（rear+1）% （k+1），其中k=4。我们计算一下上面的式子（rear+1）% （k+1）=（4 + 1）%（4 + 1）= 0。
当出数据的时候，也是让front增加的值模上（k+1）。

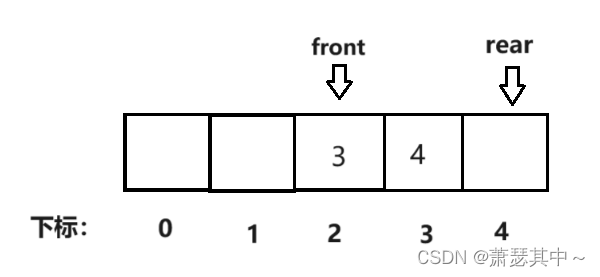
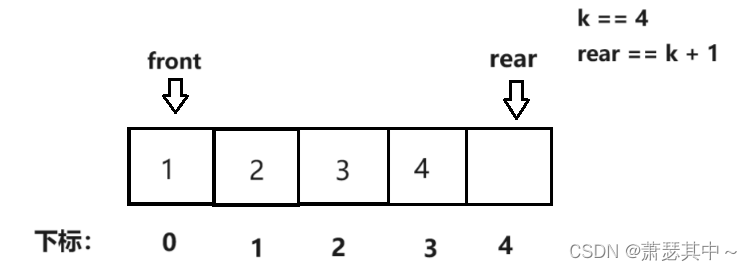
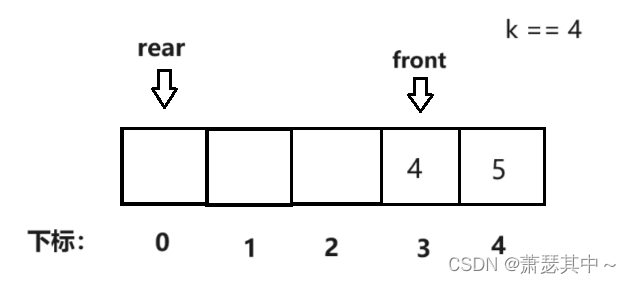
当我们要获得队尾的数据，如果是下图的第一张，小伙伴可能回想当然的，直接让rear减一，来获取数据4。但是如果是下面第二张图的情况，让rear直接减去1，就会越界。
这里采取的办法还是取模，先让rear加上k再模上k+1，写成式子就是(rear + k) % （k + 1），我们将rear=0带入，算出来的值刚好是4。

（3）各部分代码

4.3.1数据结构的设计和创造队列

循环队列以数组为底层实现结构，myCircularQueueCreate函数主要是一个初始化循环队列的操作，跟顺序表的初始化类似。

typedef struct {
    int* a;    //数组
    int front; //队头下标
    int tail;  //跟rear一样，表示队尾下标
    int k;     //循环队列的长度
} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* cq = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    cq->a = (int*)malloc(sizeof(int)*(k+1));
    cq->front = cq->tail = 0;
    cq->k = k;

    return cq;
}

4.3.2 入队列出队列

入队列和出队列要用到判空和判满，所以需要前置声明一下。

入队列先要判断队列是否满了。队列满了，返回false。不满的话，先往队尾入数据，让队尾的值加一，并且让队尾的值模上k+1。
出队列先要判断队列是都为空。队列为空，返回false。不为空的话，让front值加一，再取模k+1。

bool myCircularQueueIsEmpty(MyCircularQueue* obj);
bool myCircularQueueIsFull(MyCircularQueue* obj);

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if (myCircularQueueIsFull(obj))
        return false;

    obj->a[obj->tail] = value;
    ++obj->tail;
    obj->tail %= (obj->k+1);

    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
        return false;

    ++obj->front;
    obj->front %= (obj->k+1);
    return true;
}

4.3.3 获取队头和队尾的数据

获取队头的数据先判断队列有没有数据，有的话直接返回数组中为队头下标的元素。
获取队尾元素也是要先判断。如果队列有数据，有两种方式。第一种是如果队尾的值为0，说明此时队尾数据下标为k，需要特殊处理，如果队尾是其他值，正常返回就好。第二种是上面讲的方法，让队尾的值加上k取模k+1。

int myCircularQueueFront(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
        return -1;

    return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
        return -1;

    // if (obj->tail == 0)//特殊处理
    // {
    //     return obj->a[obj->k];
    // }
    // return obj->a[obj->tail - 1];

    int i = (obj->tail + obj->k) % (obj->k+1);
    return obj->a[i];
}

4.3.4 判空判满销毁队列

判空条件是队尾下标和队头下标相等，直接返回上述条件，如果相等，这个式子会有不为0的返回值，如果不相等，这个式子会返回0。
判满条件是队尾的值加一模上k+1，刚好等于队头的下标。
销毁队列，只要释放两个动态开辟的指针即可，顺序不能错！

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->tail;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->tail + 1) % (obj->k+1) ==obj->front;
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

总结

如果做完这四道经典OJ题目，会让更加了解栈和队列这两个数据结构。如果你对顺序表和链表感觉还有点生疏，可以看看这两篇文章，《顺序表和通讯录的实现》http://t.csdnimg.cn/Jd0b3，《单链表和双向链表的实现》http://t.csdnimg.cn/04fud。话不多说，敲起来！

创作不易，希望这篇文章能给你带来启发和帮助，如果喜欢这篇文章，请留下你的三连，你的支持的我最大的动力！！！