求n*m网格内矩形的数目 - tenos - 博客园 (cnblogs.com)

法一（题解推规律+暴力枚举得到）：

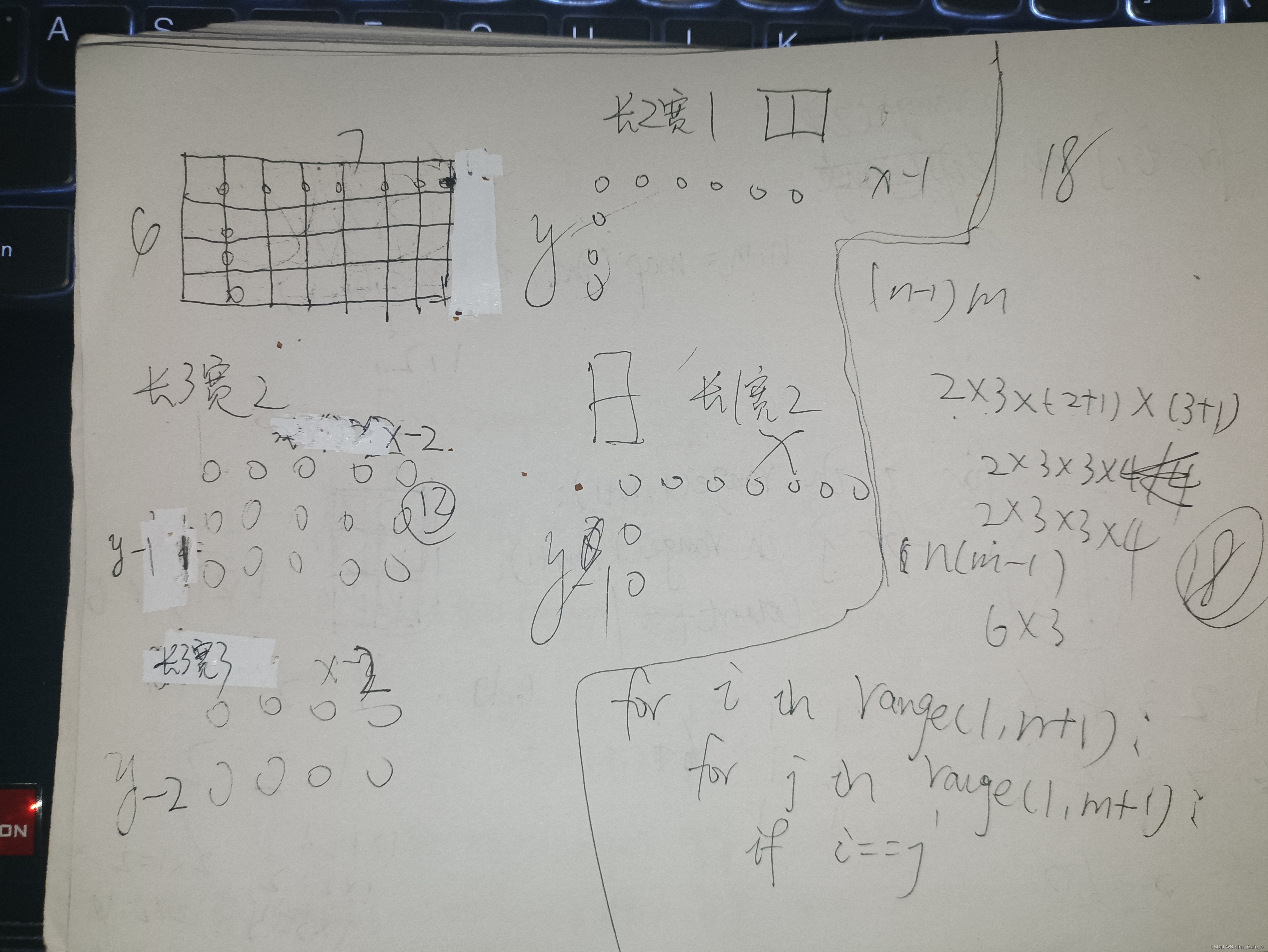
n,m=map(int,input().split())
sqr,rec=0,0 #正方形和长方形个数
#以长宽做循环，每次求n*m大小的矩形的个数
#题解是从0开始的，我这里从1开始，所以后面要+1
for i in range(1,n+1):
    for j in range(1,m+1):
        if i==j:  #正方形
            sqr+=(n-i+1)*(m-j+1)
        else:  #长方形
            rec+=(n-i+1)*(m-j+1)
print(sqr,rec,end=" ")

但是python这种方法会超时，所以用法二更好一点。

法二（公式法）：

n*m矩阵内有共有n* (n+1)/2*m* (m+1)/2个子矩形

n, m = map(int, input().split())
#这里始终要让行数<列数，要不然再后面的公式计算中会出问题，且正方形肯定要取长宽中的小数
'''
如n=3,m=5时得3*5//2*5*6//2=105
而n=5,m=3时得5*6//2*3*4//2=90就会出错
'''
if n > m: #大于就交换
    n, m = m, n
sum = int(n * m * (1+n) * (1+m) / 4) #对公式进行稍微合并
fang = 0
for i in range(1, n+1):
    fang += (n-i+1) * (m-i+1)
#因为i==j时为正方形，这个时候就只要进行单循环就行了，因为不用找长方形了
print(fang, sum-fang) #总矩形-正方形=长方形