字节期权
近日,字节跳动开启新一轮期权回购,价格微涨至 170 美元。
之前我们就写过 文章,分享历年来字节跳动的期权变化情况,这里再贴一下:
-
18年:10+ -
19年:30+ -
20年:60-70 -
21年:126 -
22年4月:140 -
22年10月:155 -
23年4月:155 -
23年10月:160
本次字节期权回购价格来到 170 美元,但仍还是从美国先开始。
字节期权仍在涨,主因是字节在 2023 年第三季度收入上涨 43%(达 309 亿美元),在广告和电商板块的增长尤其明显。
以最新数据来看,目前字节的增长速度是 Meta(前身 Facebook)的两倍。
...
以最新的汇率来计算,当时那位手握价值 900w 人民币字节期权的同学,又"少少地"涨了一点身价:

8400 股,每股涨 10 美元,以最新汇率为 7.1985 来计算。
60W,少少涨了 60W。
...
回归主线。
来一道「字节跳动」一面算法原题。
题目描述
平台:LeetCode
题号:790
有两种形状的瓷砖:一种是 2 x 1 的多米诺形,另一种是形如 "L" 的托米诺形,两种形状都可以旋转。
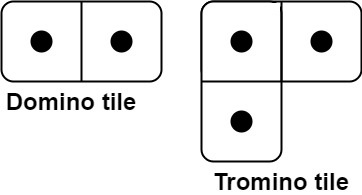
给定整数 n ,返回可以平铺 2 x n 的面板的方法的数量,返回对
取模 的值。
平铺指的是每个正方形都必须有瓷砖覆盖。
两个平铺不同,当且仅当面板上有四个方向上的相邻单元中的两个,使得恰好有一个平铺有一个瓷砖占据两个正方形。
示例 1: 
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。
示例 2:
输入: n = 1
输出: 1
提示:
状态机 DP
定义 为无须考虑前 列(含义为前 列已铺满),当前第 列状态为 时的方案数。
其中 取值范围为 分别对应了当前列的填充情况:
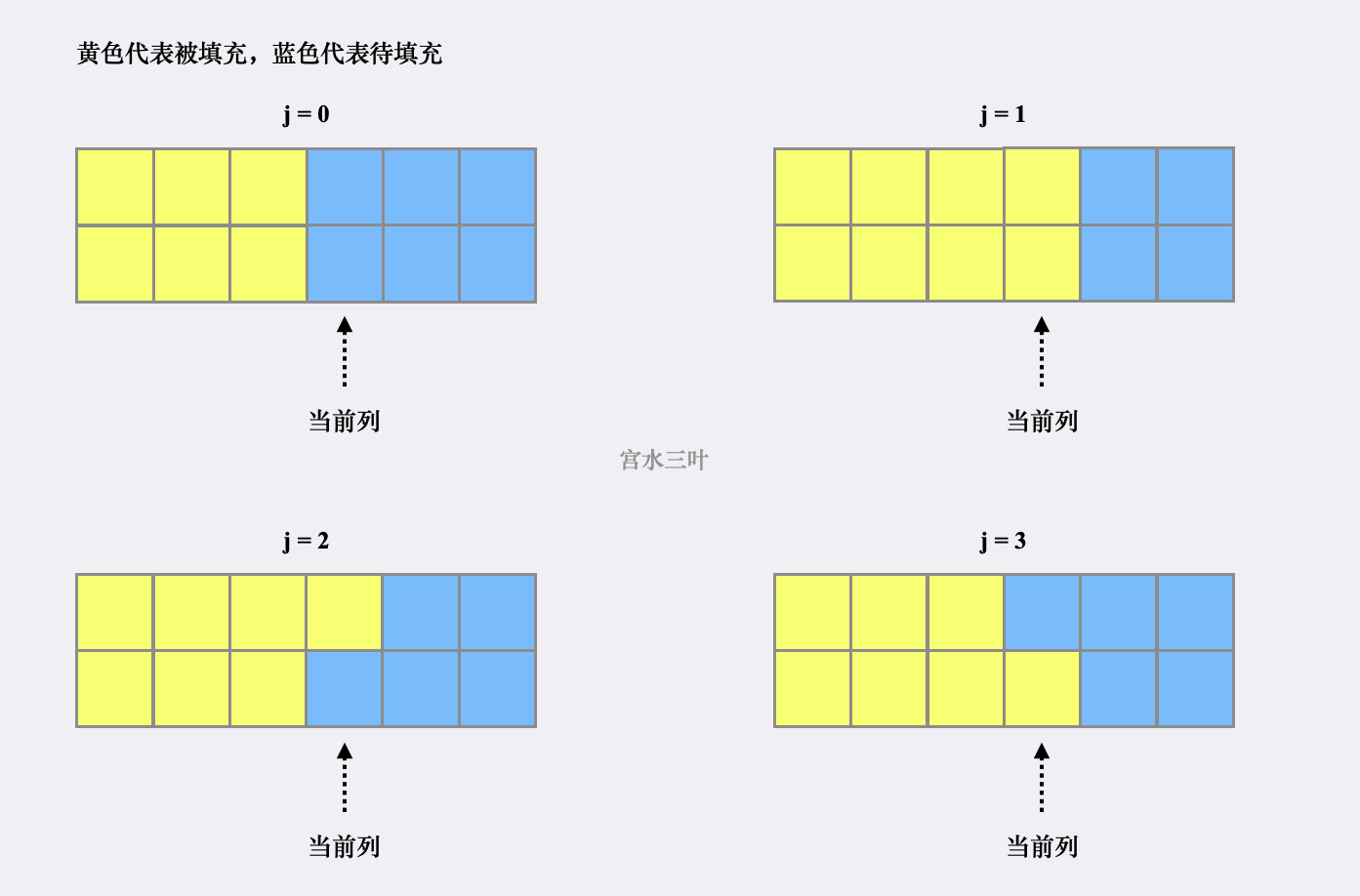
为了方便,我们人为规定列数从 开始。
由于骨牌只能在 的棋盘内填充(不能延伸出棋盘两端),因此我们有显而易见的初始化状态:
分别对应「第一列不放置任何骨牌」和「第一列竖着放一块 骨牌」合法方案。
而 和 由于没法在棋盘左侧以外的位置放置骨牌,不存在合法方案,其值均为 。
同时可知 为我们最终答案,含义为所有列都恰好铺完,不溢出棋盘右侧位置。
不失一般性考虑 该如何计算,其实就是一个简单的状态机转移分情况讨论:
-
: 需要前 列铺满,同时第 列没有被铺,只能由 转移而来,即有
❝
这里需要尤其注意:虽然我们能够在上一步留空第 列,然后在 列竖放一块 的骨牌(如下图)
❞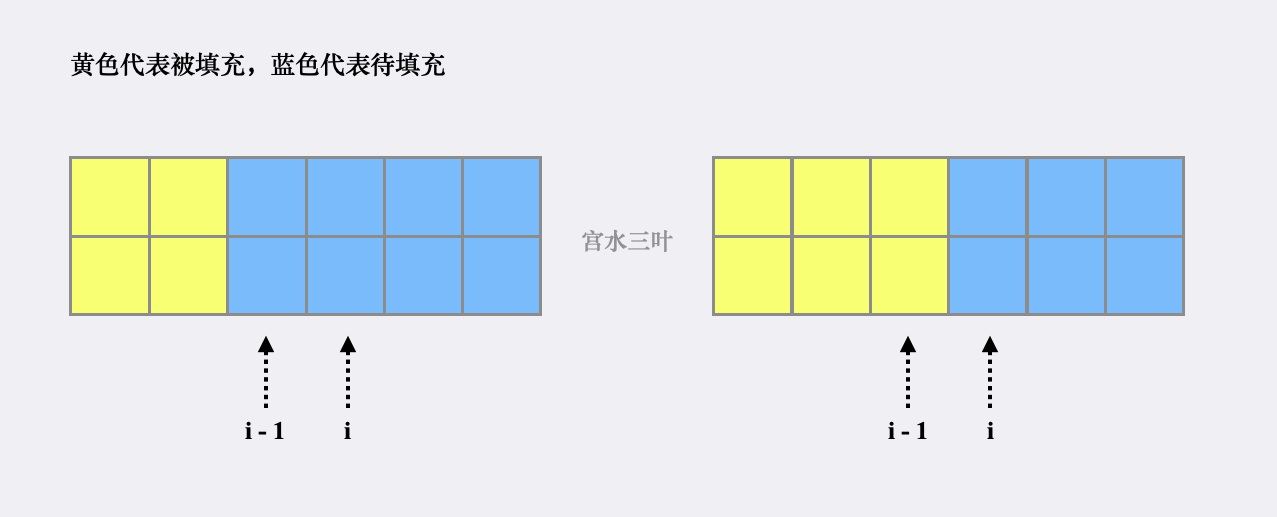
❝
但我们不能从 转移到 ,因为此时放置的骨牌,仅对第 列产生影响,不会对第 列产生影响,该决策所产生的方案数,已在 时被统计
❞ -
: 可由 转移而来(见下图),其中 ,即有
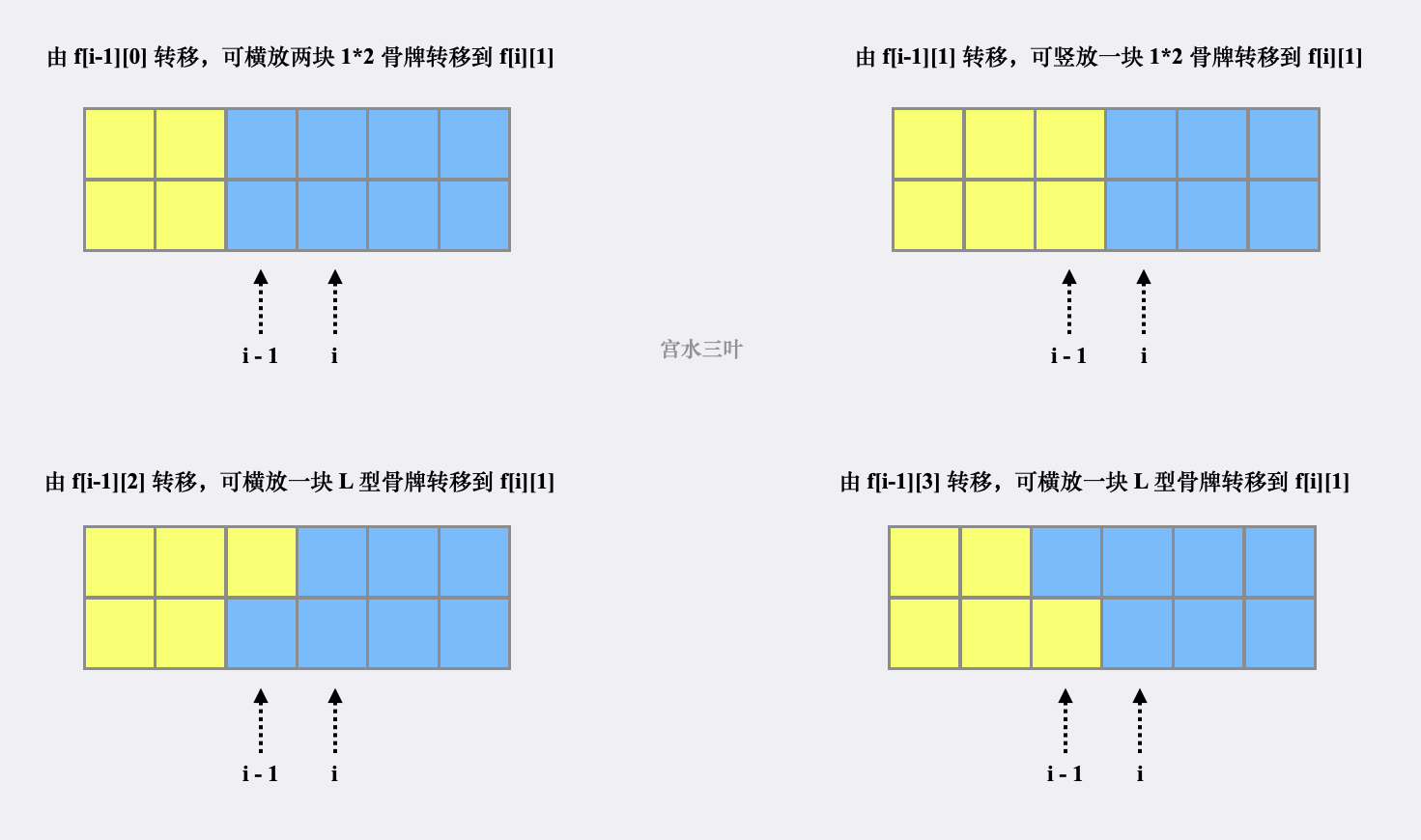
-
: 可由 和 转移而来
-
: 可由 和 转移而来
Java 代码:
class Solution {
int MOD = (int)1e9+7;
public int numTilings(int n) {
int[][] f = new int[n + 10][4];
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= n; i++) {
f[i][0] = f[i - 1][1];
int cur = 0;
for (int j = 0; j < 4; j++) cur = (cur + f[i - 1][j]) % MOD;
f[i][1] = cur;
f[i][2] = (f[i - 1][0] + f[i - 1][3]) % MOD;
f[i][3] = (f[i - 1][0] + f[i - 1][2]) % MOD;
}
return f[n][1];
}
}
C++ 代码:
class Solution {
const int MOD = 1e9 + 7;
public:
int numTilings(int n){
vector<vector<int>> f(n + 10, vector<int>(4));
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= n; ++i){
f[i][0] = f[i - 1][1];
int cur = 0;
for (int j = 0; j < 4; ++j) cur = (cur + f[i - 1][j]) % MOD;
f[i][1] = cur;
f[i][2] = (f[i - 1][0] + f[i - 1][3]) % MOD;
f[i][3] = (f[i - 1][0] + f[i - 1][2]) % MOD;
}
return f[n][1];
}
};
Python3 代码:
class Solution:
def numTilings(self, n: int) -> int:
f = [[0] * 4 for _ in range(n + 10)]
f[1][0] = f[1][1] = 1
for i in range(2, n + 1):
f[i][0] = f[i - 1][1]
f[i][1] = sum([f[i - 1][j] for j in range(4)])
f[i][2] = f[i - 1][0] + f[i - 1][3]
f[i][3] = f[i - 1][0] + f[i - 1][2]
return f[n][1] % 1000000007
TypeScript 代码:
function numTilings(n: number): number {
const MOD = 1e9+7
const f = new Array<Array<number>>()
for (let i = 0; i <= n; i++) f[i] = new Array<number>(4).fill(0)
f[1][0] = f[1][1] = 1
for (let i = 2; i <= n; i++) {
f[i][0] = f[i - 1][1]
let cur = 0
for (let j = 0; j < 4; j++) cur = (cur + f[i - 1][j]) % MOD
f[i][1] = cur
f[i][2] = (f[i - 1][0] + f[i - 1][3]) % MOD
f[i][3] = (f[i - 1][0] + f[i - 1][2]) % MOD
}
return f[n][1]
}
-
时间复杂度: -
空间复杂度:
滚动数组优化
利用 仅依赖于 ,我们可以采用「滚动数组」方式将其空间优化至 。
Java 代码:
class Solution {
int MOD = (int)1e9+7;
public int numTilings(int n) {
int[][] f = new int[2][4];
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= n; i++) {
int a = i & 1, b = (i - 1) & 1;
f[a][0] = f[b][1];
int cur = 0;
for (int j = 0; j < 4; j++) cur = (cur + f[b][j]) % MOD;
f[a][1] = cur;
f[a][2] = (f[b][0] + f[b][3]) % MOD;
f[a][3] = (f[b][0] + f[b][2]) % MOD;
}
return f[n & 1][1];
}
}
C++ 代码:
class Solution {
const int MOD = 1e9 + 7;
public:
int numTilings(int n){
vector<vector<int>> f(2, vector<int>(4));
f[1][0] = f[1][1] = 1;
for (int i = 2; i <= n; ++i){
int a = i & 1, b = (i - 1) & 1;
f[a][0] = f[b][1];
int cur = 0;
for (int j = 0; j < 4; ++j) cur = (cur + f[b][j]) % MOD;
f[a][1] = cur;
f[a][2] = (f[b][0] + f[b][3]) % MOD;
f[a][3] = (f[b][0] + f[b][2]) % MOD;
}
return f[n & 1][1];
}
};
Python3 代码:
class Solution:
def numTilings(self, n: int) -> int:
f = [[0] * 4 for _ in range(2)]
f[1][0] = f[1][1] = 1
for i in range(2, n + 1):
a, b = i & 1, (i - 1) & 1
f[a][0] = f[b][1]
f[a][1] = sum([f[b][j] for j in range(4)])
f[a][2] = f[b][0] + f[b][3]
f[a][3] = f[b][0] + f[b][2]
return f[n & 1][1] % 1000000007
TypeScript 代码:
function numTilings(n: number): number {
const MOD = 1e9+7
const f = new Array<Array<number>>()
for (let i = 0; i <= 1; i++) f[i] = new Array<number>(4).fill(0)
f[1][0] = f[1][1] = 1
for (let i = 2; i <= n; i++) {
const a = i & 1, b = (i - 1) & 1
f[a][0] = f[b][1]
let cur = 0
for (let j = 0; j < 4; j++) cur = (cur + f[b][j]) % MOD
f[a][1] = cur
f[a][2] = (f[b][0] + f[b][3]) % MOD
f[a][3] = (f[b][0] + f[b][2]) % MOD
}
return f[n & 1][1]
}
-
时间复杂度: -
空间复杂度:
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉