1. 引言
CGAL 的目标是精确计算非线性对象,特别是定义在代数曲线和曲面上的对象。因此,表示多项式、代数扩展和有限域的类型在相关的实现中扮演着更加重要的角色。为了跟上这些变化,我们引入了这个软件包。由于引入的框架必须特别支持多项式,因此本软件包避免使用数字类型这一术语。相反,软件包区分了类型的代数结构和类型是否可嵌入实数轴,简称实数可嵌入。此外,软件包还引入了可互操作类型的概念,允许明确处理混合操作。
2 代数结构
本节所介绍的代数结构概念来自传统代数中众所周知的对应概念,但我们也必须向现有的类型及其限制致敬。为了保持界面的最小化,我们不希望涵盖所有已知的代数结构,例如,我们没有引入群这样的基本结构概念,也没有引入倾斜域这样的特殊结构概念。
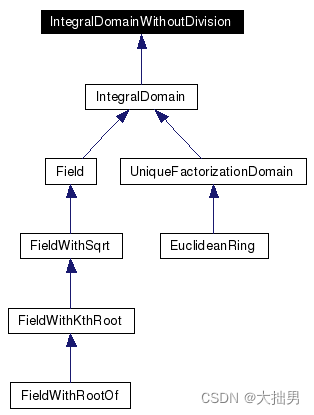
Figure 1.1 Concept Hierarchy of Algebraic Structures
图 1.1 显示了代数结构概念的细化关系。IntegralDomain(积分域)、UniqueFactorizationDomain(唯一因式分解域)、EuclideanRing(欧几里得环)和 Field(场)对应于同名的代数结构。FieldWithSqrt、FieldWithKthRoot 和 FieldWithRootOf 是分别在 "sqrt"、"k-th root "和 "多项式实根 "运算下封闭的域。概念 IntegralDomainWithoutDivision 也对应于代数意义上的积分域,两者的区别在于某些积分域的实现缺乏(代数上总是定义明确的)积分除法。请注意,Field 精炼了 IntegralDomain。这是因为大多数环论概念,如最大公有除数,对 Field 来说都是微不足道的。因此,我们认为 Field 是对 IntegralDomain 的完善,而不是对更高级的环概念的完善。如果一种算法想要依赖 gcd 或余数计算,那么它就在试图做一些本来不应该在域中做的事情。
代数结构的主要属性收集在代数结构属性(Algebraic_structure_traits)类中。具体来说,每个具体模型 AS 所满足的(最精炼的)概念都编码在标签 Algebraic_structure_traits<AS>::Algebraic_category 中。代数结构至少是可赋值的、可复制构造的、可默认构造的和可等价比较的。此外,我们还要求代数结构可由 int 构建。为了使用方便,而且由于它们的语义足够标准,我们假定它们的存在,通常的算术运算符和比较运算符需要通过 C++ 运算符重载来实现。除法运算符保留给字段中的除法运算。所有其他一元函数(如 sqrt)和二元函数(如 gcd-求两个数的最大公约数、div)必须是众所周知的 STL 概念 AdaptableUnaryFunction 或 AdaptableBinaryFunction 概念的模型,并且是 traits 类的局部函数(如 Algebraic_structure_traits<AS>::Sqrt()(x) )。这种设计使我们能够从 STL 的所有部分及其编程风格中获益,并避免了使用重载函数的旧设计所遇到的名称查找和两次模板编译问题。不过,为了便于使用和向后兼容,所有功能都可以通过定义在 CGAL 命名空间中的全局函数来访问,例如 CGAL::sqrt(x) 。这可以通过函数模板使用 traits 类的相应函数来实现。有关概述,请参阅参考手册中的 "代数基础参考 "部分。
2.2 代数类别
对于 AS 类型,Algebraic_structure_traits<AS> 提供了几个标签。最重要的标签是 "代数类别"(Algebraic_category)标签,它表示 AS 类型满足的最精细的代数概念。该标签可以是:Integral_domain_without_division_tag、Integral_domain_tag、Field_tag、Field_with_sqrt_tag、Field_with_kth_root_tag、Field_with_root_of_tag、Unique_factorization_domain_tag、Euclidean_ring_tag,甚至是 Null_tag 中的一个,以防该类型不是代数结构概念的模型。这些标记相互派生,以反映代数结构概念的层次,例如,Field_with_sqrt_tag 从 Field_tag 派生。
2.3 精确和对数字敏感
此外,Algebraic_structure_traits<AS> 还提供了 Is_exact 和 Is_numerical_sensitive 这两个布尔标签。
如果代数结构概念所要求的所有运算都经过计算,且两个代数表达式的比较总是正确的,那么该代数结构就被认为是精确的。
如果代数结构的性能对算法的条件数敏感,则该代数结构被视为数值敏感结构。请注意,这两个概念其实是有区别的,例如,基本类型 int 并不是数值敏感型,而是由于溢出而被认为是不精确型。相反,leda_real 或 CORE::Expr 类型是精确的,但由于内部使用了多精度浮点运算,因此对数值问题很敏感。我们希望 Is_numerical_sensitive 用于算法的调度,而 Is_exact 则用于启用仅对精确类型进行检查的断言。
标签在调度不同实现时非常有用。下面的示例说明了使用重载函数对 Fields 进行调度。由于代数类别标记反映了代数结构层次,因此该示例只需要两个重载函数。
Algebraic_foundations/algebraic_structure_dispatch.cpp
#include <CGAL/IO/io.h>
#include <CGAL/Algebraic_structure_traits.h>
#include <CGAL/number_utils.h>
#include <CGAL/int.h>
template< typename NT > NT unit_part(const NT& x);
template< typename NT >
NT unit_part_(const NT& x, CGAL::Field_tag);
template< typename NT >
NT unit_part_(const NT& x, CGAL::Integral_domain_without_division_tag);
template< typename NT >
NT unit_part(const NT& x){
// the unit part of 0 is defined as 1.
if (x == 0 ) return NT(1);
typedef CGAL::Algebraic_structure_traits<NT> AST;
typedef typename AST::Algebraic_category Algebraic_category;
return unit_part_(x,Algebraic_category());
}
template< typename NT >
NT unit_part_(const NT& x, CGAL::Integral_domain_without_division_tag){
// For many other types the only units are just -1 and +1.
return NT(int(CGAL::sign(x)));
}
template< typename NT >
NT unit_part_(const NT& x, CGAL::Field_tag){
// For Fields every x != 0 is a unit.
// Therefore, every x != 0 is its own unit part.
return x;
}
int main(){
// Function call for a model of EuclideanRing, i.e. int.
std::cout<< "int: unit_part(-3 ): " << unit_part(-3 ) << std::endl;
// Function call for a model of FieldWithSqrt, i.e. double
std::cout<< "double: unit_part(-3.0): " << unit_part(-3.0) << std::endl;
return 0;
}
// Note that this is just an example
// This implementation for unit part won't work for some types, e.g.,
// types that are not RealEmbeddable or types representing structures that have
// more units than just -1 and +1. (e.g. MP_Float representing Z[1/2])
// From there Algebraic_structure_traits provides the functor Unit_part.3 可嵌入的实数
大多数数字类型代表实数的某个子集。我们希望这些类型具有计算符号、绝对值或双近似值的功能。特别是,我们可以期望在这种类型上有一个反映沿实数轴顺序的阶。所有这些属性都集合在 RealEmbeddable 概念中。这个概念与代数结构概念是正交的,也就是说,一个类型可能只是 RealEmbeddable 的一个模型,因为这个类型可能只是表示实数轴上的值,而不提供任何算术运算。
至于代数结构,这一概念也是面向特质类的。与 RealEmbeddable 相关的主要功能都集中在 Real_embeddable_traits 类中。特别是,它提供了一个布尔标记 Is_real_embeddable,用于指示一个类型是否是 RealEmbeddable 的模型。比较运算符需要通过 C++ 运算符重载来实现。所有一元函数(如 sign、to_double)和二元函数(如 compare )都是 STL 概念 AdaptableUnaryFunction 和 AdaptableBinaryFunction 的模型,并且是 Real_embeddable_traits 的局部函数。
如果一个类型是 "整除域"(IntegralDomainWithoutDivision)和 "实数可嵌入"(RealEmbeddable)的模型,那么这个类型的对象所代表的数在算术和比较中是相同的。由此可见,该类型所代表的环是整数的超集和实数的子集,因此特征为零。
如果该类型是 Field 和 RealEmbeddable 的模型,那么它就是有理数的超集。
4 实数类型
每个 CGAL 内核都有两个实数类型(可嵌入实数的数字类型)。其中一个是 FieldNumberType,另一个是 RingNumberType。基本内核对象(点、矢量等)的坐标来自这两种类型之一(笛卡尔内核为 FieldNumberType,齐次坐标内核为 RingNumberType)。
概念 FieldNumberType 结合了概念 Field 和 RealEmbeddable 的要求,而 RingNumberType 则结合了 IntegralDomainWithoutDivision 和 RealEmbeddable 的要求。从代数学角度看,实数类型并不形成独特的结构,因此未列入图 1.1 的概念层次结构中。
5 互操作性
本节介绍类型互操作性的两个概念,即 ImplicitInteroperable 和 ExplicitInteroperable。虽然 ExplicitInteroperable 是基本概念,但我们还是从 ImplicitInteroperable 开始,因为它更直观。
一般来说,混合操作由重载操作符和函数提供,或仅通过隐式构造函数调用提供。ImplicitInteroperable 概念就反映了这种互操作性。然而,在模板代码中,混合运算的结果类型或所谓的强制类型可能并不明确。因此,软件包引入了 Coercion_traits,通过 Coercion_traits<A,B>::Type 访问两个互操作类型 A 和 B 的强制类型。
一些微不足道的例子是使用胁迫类型 double 的 int 和 double,或者使用胁迫类型 Gmpq 的 Gmpz 和 Gmpq。然而,胁迫类型并不一定是输入类型之一,例如,一个有理类型乘以整数系数的多项式的胁迫类型应该是一个有理系数的多项式。
Coercion_traits 还需要提供一个函数 Coercion_traits<A,B>::Cast(),用于将输入类型转换为强制类型。这实际上是更基本的概念 ExplicitInteroperable 的核心。引入 ExplicitInteroperable 是为了涵盖更复杂的情况,在这些情况下,很难或不可能保证隐式互操作性。请注意,这个函数对 ImplicitInteroperable 类型也很有用,因为它可以用来取消多余的类型转换。
如果两个类型 A 和 B 与强制类型 C 是 ExplicitInteroperable 的,那么对于由 C 的 Algebraic_structure_traits 和 Real_embeddable_traits 提供的所有二进制函数,它们都是有效的参数类型。
5.1 examples
The following example illustrates how two write code for ExplicitInteroperable types.
Algebraic_foundations/interoperable.cpp
#include <CGAL/Coercion_traits.h>
#include <CGAL/IO/io.h>
// this is an implementation for ExplicitInteroperable types
// the result type is determined via Coercion_traits<A,B>
template <typename A, typename B>
typename CGAL::Coercion_traits<A,B>::Type
binary_func(const A& a , const B& b){
typedef CGAL::Coercion_traits<A,B> CT;
// check for explicit interoperability
CGAL_static_assertion((CT::Are_explicit_interoperable::value));
// CT::Cast is used to to convert both types into the coercion type
typename CT::Cast cast;
// all operations are performed in the coercion type
return cast(a)*cast(b);
}
int main(){
// Function call for the interoperable types
std::cout<< binary_func(double(3), int(5)) << std::endl;
// Note that Coercion_traits is symmetric
std::cout<< binary_func(int(3), double(5)) << std::endl;
return 0;
}下面的示例说明了 ImplicitInteroperable 和 ExplicitInteroperable 类型的调度。二元运算函数(只是乘以两个参数)应该接受两个 ExplicitInteroperable 参数。对于 ImplicitInteroperable 类型,我们选择了一种避免显式转换的变体。
Algebraic_foundations/implicit_interoperable_dispatch.cpp
#include <CGAL/Coercion_traits.h>
#include <CGAL/Quotient.h>
#include <CGAL/Sqrt_extension.h>
#include <CGAL/IO/io.h>
// this is the implementation for ExplicitInteroperable types
template <typename A, typename B>
typename CGAL::Coercion_traits<A,B>::Type
binary_function_(const A& a , const B& b, CGAL::Tag_false){
std::cout << "Call for ExplicitInteroperable types: " << std::endl;
typedef CGAL::Coercion_traits<A,B> CT;
typename CT::Cast cast;
return cast(a)*cast(b);
}
// this is the implementation for ImplicitInteroperable types
template <typename A, typename B>
typename CGAL::Coercion_traits<A,B>::Type
binary_function_(const A& a , const B& b, CGAL::Tag_true){
std::cout << "Call for ImpicitInteroperable types: " << std::endl;
return a*b;
}
// this function selects the correct implementation
template <typename A, typename B>
typename CGAL::Coercion_traits<A,B>::Type
binary_func(const A& a , const B& b){
typedef CGAL::Coercion_traits<A,B> CT;
typedef typename CT::Are_implicit_interoperable Are_implicit_interoperable;
return binary_function_(a,b,Are_implicit_interoperable());
}
int main(){
CGAL::IO::set_pretty_mode(std::cout);
// Function call for ImplicitInteroperable types
std::cout<< binary_func(double(3), int(5)) << std::endl;
// Function call for ExplicitInteroperable types
CGAL::Quotient<int> rational(1,3); // == 1/3
CGAL::Sqrt_extension<int,int> extension(1,2,3); // == 1+2*sqrt(3)
CGAL::Sqrt_extension<CGAL::Quotient<int>,int> result = binary_func(rational, extension);
std::cout<< result << std::endl;
return 0;
}6 分数
除了需要对对象整体进行代数运算外,人们还希望将一些数字类型分解为分子和分母。这不仅适用于有理数(如 Quotient、Gmpq、mpq_class 或 leda_rational),也适用于复合对象(如 Sqrt_extension 或 Polynomial),它们可以分解为(标量)分母和具有更简单系数类型(如整数而非有理数)的复合分子。通常,对这些无分母倍数进行运算的速度会更快。如果类型是分数,相关功能以及分子和分母类型由 Fraction_traits 提供。特别是 Fraction_traits 提供了一个 Is_fraction 标签,可用于分派。
出于向后兼容的考虑,我们保留了一个相关的类 Rational_traits。不过,我们建议使用 Fraction_traits,因为它更通用,而且提供了分派功能。
The following example show a simple use of Fraction_traits:
File Algebraic_foundations/fraction_traits.cpp
#include <CGAL/Fraction_traits.h>
#include <CGAL/IO/io.h>
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
#include <CGAL/Gmpq.h>
int main(){
typedef CGAL::Fraction_traits<CGAL::Gmpq> FT;
typedef FT::Numerator_type Numerator_type;
typedef FT::Denominator_type Denominator_type;
CGAL_static_assertion((std::is_same<Numerator_type,CGAL::Gmpz>::value));
CGAL_static_assertion((std::is_same<Denominator_type,CGAL::Gmpz>::value));
Numerator_type numerator;
Denominator_type denominator;
CGAL::Gmpq fraction(4,5);
FT::Decompose()(fraction,numerator,denominator);
CGAL::IO::set_pretty_mode(std::cout);
std::cout << "decompose fraction: "<< std::endl;
std::cout << "fraction : " << fraction << std::endl;
std::cout << "numerator : " << numerator<< std::endl;
std::cout << "denominator: " << denominator << std::endl;
std::cout << "re-compose fraction: "<< std::endl;
fraction = FT::Compose()(numerator,denominator);
std::cout << "fraction : " << fraction << std::endl;
}
#else
int main(){ std::cout << "This examples needs GMP" << std::endl; }
#endif下面的示例说明了一个向量(即多项式的系数向量)的积分。请注意,为了使系数增长最小化,Fraction_traits<Type>::Common_factor 被用来计算分母的最小公倍数。
File Algebraic_foundations/integralize.cpp
#include <CGAL/Fraction_traits.h>
#include <CGAL/IO/io.h>
#include <vector>
#include <CGAL/number_utils.h>
template <class Fraction>
std::vector<typename CGAL::Fraction_traits<Fraction>::Numerator_type >
integralize(
const std::vector<Fraction>& vec,
typename CGAL::Fraction_traits<Fraction>::Denominator_type& d
) {
typedef CGAL::Fraction_traits<Fraction> FT;
typedef typename FT::Numerator_type Numerator_type;
typedef typename FT::Denominator_type Denominator_type;
typename FT::Decompose decompose;
std::vector<Numerator_type> num(vec.size());
std::vector<Denominator_type> den(vec.size());
// decompose each coefficient into integral part and denominator
for (unsigned int i = 0; i < vec.size(); i++) {
decompose(vec[i], num[i], den[i]);
}
// compute 'least' common multiple of all denominator
// We would like to use gcd, so let's think of Common_factor as gcd.
typename FT::Common_factor gcd;
d = 1;
for (unsigned int i = 0; i < vec.size(); i++) {
d *= CGAL::integral_division(den[i], gcd(d, den[i]));
}
// expand each (numerator, denominator) pair to common denominator
for (unsigned int i = 0; i < vec.size(); i++) {
// For simplicity ImplicitInteroperability is expected in this example
num[i] *= CGAL::integral_division(d, den[i]);
}
return num;
}
#ifdef CGAL_USE_GMP
#include <CGAL/Gmpz.h>
#include <CGAL/Gmpq.h>
int main(){
std::vector<CGAL::Gmpq> vec(3);
vec[0]=CGAL::Gmpq(1,4);
vec[1]=CGAL::Gmpq(1,6);
vec[2]=CGAL::Gmpq(1,10);
std::cout<< "compute an integralized vector" << std::endl;
std::cout<<"input vector: ["
<< vec[0] << "," << vec[1] << "," << vec[2] << "]" << std::endl;
CGAL::Gmpz d;
std::vector<CGAL::Gmpz> integral_vec = integralize(vec,d);
std::cout<<"output vector: ["
<< integral_vec[0] << ","
<< integral_vec[1] << ","
<< integral_vec[2] << "]" << std::endl;
std::cout<<"denominator : "<< d <<std::endl;
}
#else
int main(){ std::cout << "This examples needs GMP" << std::endl; }
#endif7 设计和实现的历史
该软件包自 3.3 版起成为 CGAL 的一部分。当然,该软件包是以 CGAL 以前的 Number 类型支持为基础的。这要追溯到 Stefan Schirra 和 Andreas Fabri。但另一方面,该软件包在很大程度上受到了 Exacus [1] 中数字类型支持经验的影响,这主要可以追溯到 Lutz Kettner、Susan Hert、Arno Eigenwillig 和 Michael Hemmer。不过,该软件包抽象出了对嵌入实轴的数字类型的纯粹支持,从而也允许支持多项式、有限域和代数扩展。另请参见后续相关章节。









![Linux基础命令[11]-find](https://img-blog.csdnimg.cn/direct/77fe8b0071724e5486b80920388136f0.png)