题目

最小栈

请你设计一个最小栈。它提供push，pop，top操作，并能在常数时间内检索到最小元素的栈。

实现MinStack类:

• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。
  示例 1:

输入: ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[2],[-3],[],[],[],[]]
输出: [null,null,null,null,-3,null,2,-2]
解释: MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(2); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 2. minStack.getMin(); --> 返回 -2.

提示:

-231 <= val <= 231 - 1 pop、top 和 getMin 操作总是在 非空栈 上调用 push、pop、top 和 getMin 最多被调用 3 * 104 次

注意： 本题与主站 155 题相同：https://leetcode-cn.com/problems/min-stack/

解法1：使用 map 排序并统计

• 利用 map 自动排序的特点，将栈元素值作为 key，压栈时对应的 key 的 value 自增，需要查询最小值的时候返回第一个元素即可
• 出栈时，对应的 key 的 value 自减，为 0 时则删除这个键值对，表示栈中没有这个数值的元素
• 这个解法的缺点是，保存了所有元素的计数值，但是其实有一些元素的计数值是不需要保存的，解法2 解决了这个问题

class MinStack {
    vector<int> vec;
    map<int,int> m;

public:
    /** initialize your data structure here. */
    MinStack() {

    }
    
    void push(int x) {
        vec.push_back(x);
        if(m.find(x)==m.end()) m[x]=1;
        else m[x]++;
    }
    
    void pop() {
        int temp = vec.back();
        vec.pop_back();
        if(!(--m[temp])) m.erase(temp);
    }
    
    int top() {
        return *(vec.end()-1);
    }
    
    int getMin() {
        return (*m.begin()).first;
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(x);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();
 */

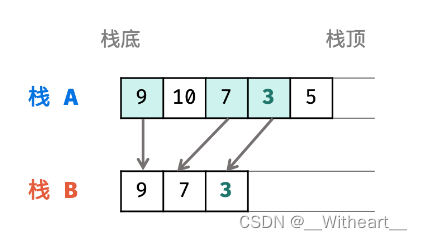
解法2：只保留每个时刻栈中的最小元素

• 由于出栈必须按照一定的顺序，所以只需要在入栈的时候保存每一次入栈后的最小值，就可以方便地在出栈的时候进行最小值的更新
  

class MinStack {
    stack<int> s, minS;
public:
    /** initialize your data structure here. */
    MinStack() {

    }
    
    void push(int x) {
        s.push(x);
        if(minS.empty() || minS.top()>=x) minS.push(x);
    }
    
    void pop() {
        if(minS.top()==s.top()) minS.pop();
        s.pop();
    }
    
    int top() {
        return s.top();
    }
    
    int getMin() {
        return minS.top();
    }
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(x);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();
 */