曲线 Curves是 Photoshop 中强大的色彩调整工具,提供了对图像亮度和颜色的精细控制,正确使用曲线可以显著改善图像的质量和风格。
Ps菜单:图像/调整/曲线
Image/Adjustments/Curves
快捷键:Ctrl + M
Ps菜单:图层/新建调整图层/曲线
New Adjustment Layer/Curves
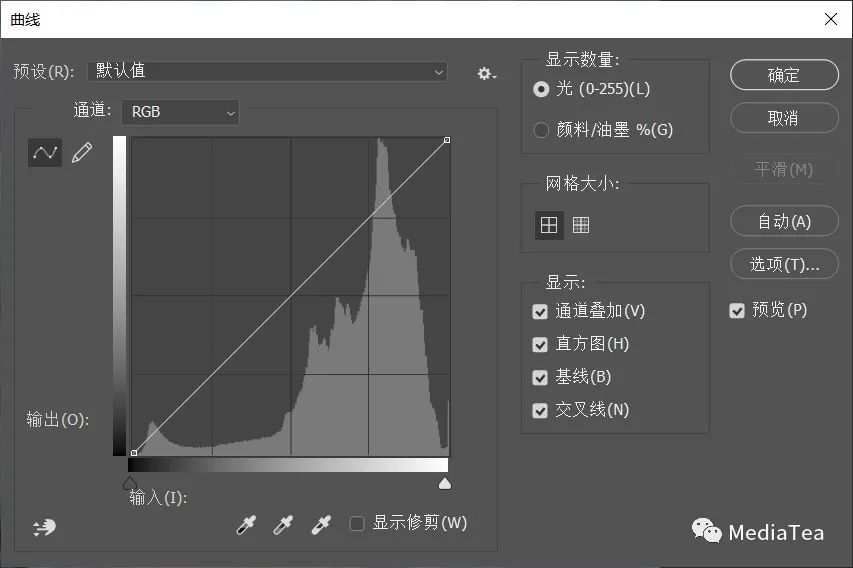
曲线调整命令对话框
曲线调整命令可以直接作用于图层、通道或蒙版上,是一种破坏性的编辑。
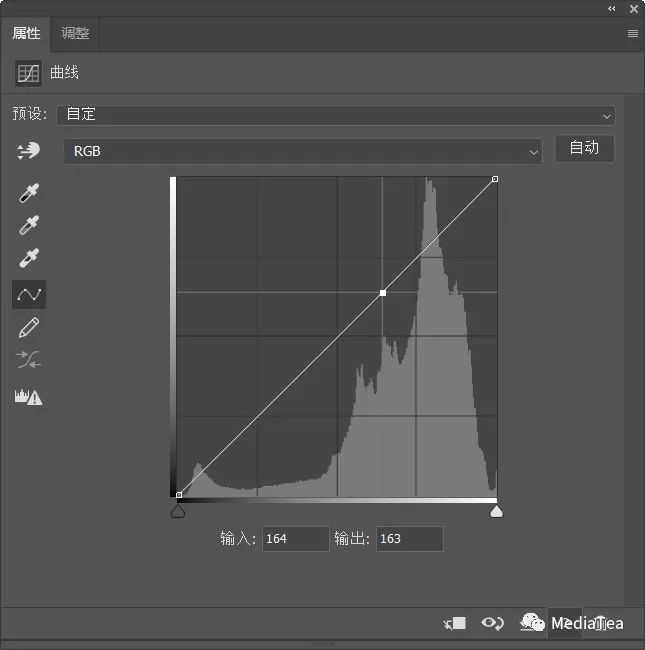
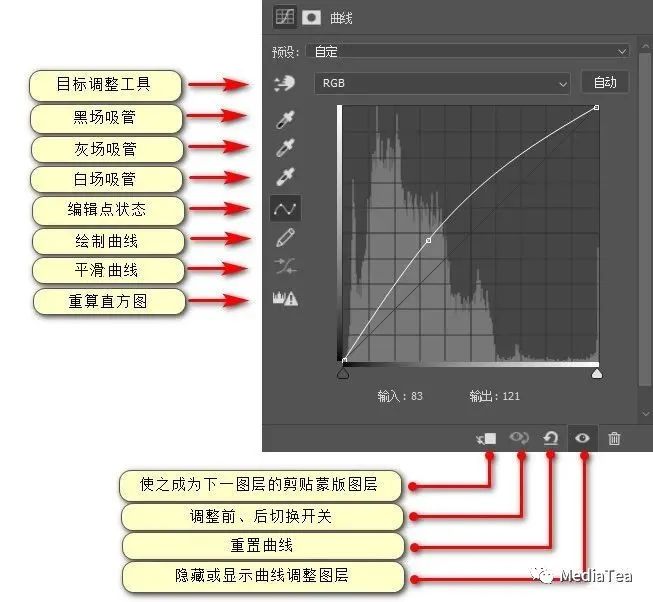
曲线调整图层的“属性”面板
曲线调整命令对话框右侧的选项(如显示修剪、显示选项等),可在曲线调整图层的“属性”面板控制菜单中找到。
◆ ◆ ◆
使用方法与技巧
1、在曲线上通过添加控制点,然后拖动或编辑这些控制点就可实现对图像的精细调整。
请参阅:
《Ps:曲线的基本操作》
2、在图像上取样时,按住 Shift 键则转换为颜色取样器工具,在图像上单击,可添加取样点。
通过“信息”面板比较取样点在调整前后的值,常用于确定中性色或解决偏色等问题。
按住 Alt + Shift 键点击画布上的取样点,可删除之。
3、使用曲线调整命令可对通道、蒙版进行处理。还可选中两个原色通道进行处理。
比如、在“通道”面板上同时选中红通道和绿通道之后,按快捷键 Ctrl + M 调用曲线调整命令。
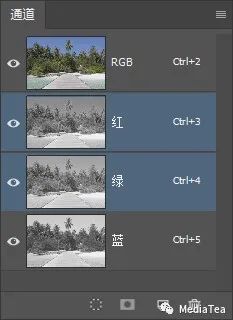
此时,曲线将同时处理红绿(RG)通道。
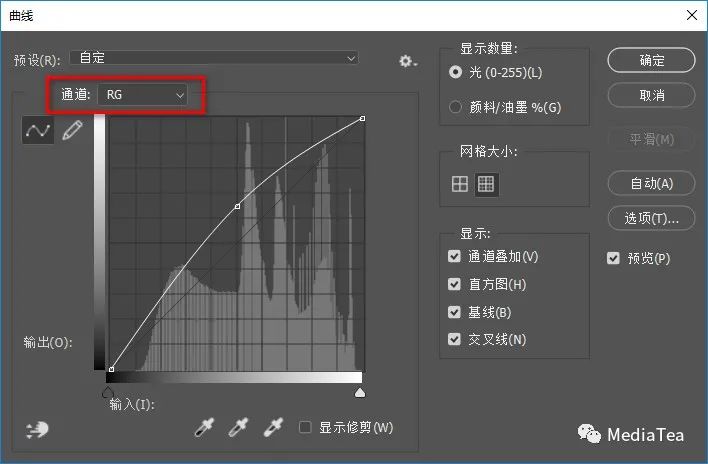
提示:
红绿通道曲线往左上走是增加黄色,与单独调整蓝通道曲线来增加黄色的效果、范围是不一样的。
◆ ◆ ◆
命令选项说明
预设
Presets
用于选择或自定义预设。
通道
Channel
颜色模式(比如,RGB、CMYK、Lab、灰度、双色调等)的不同影响了曲线的坐标系、可调整的通道以及可实现的效果。
比如,在 RGB 颜色模式下,通道选项有四项:RGB(复合通道)、红、绿、蓝通道。
请参阅:
《Ps:认识 RGB 曲线》
自动
Auto
点击此按钮,可依据自动颜色校正算法自动调节曲线。
请参阅:
《Ps:自动调整命令与自动颜色校正选项》
输入
Input
对应横坐标,表示调整前的值。
输出
Output
对应纵坐标,表示调整后的值。
目标调整工具
Targeted Adjustment Tool
启用“目标调整工具”后,直接在图像上点击就可以添加控制点,若按住鼠标不放并上下移动可进行调整。
黑场吸管
Black Point Eyedropper
选取图像中应被视为最暗点的颜色,用于设置黑场。
点击图像中特定的点后,将自动调整原色通道曲线使该点变为纯黑色。
按住 Alt 键时,将自动显示阴影剪切。
灰场吸管
Gray Point Eyedropper
选取图像中本来应该是灰色的颜色,将其校正为灰色。
点击图像中特定的点后,将自动调整原色通道曲线使该点变为无颜色。
可以将灰场吸管理解为白平衡校正器。
白场吸管
White Point Eyedropper
选取图像中应被视为最亮点的颜色,用于设置白场。
点击图像中特定的点后,将自动调整原色通道曲线使该点变为纯白色。
按住 Alt 键时,将自动显示高光剪切。
编辑点模式
Edit Points
默认模式,通过控制点来调节曲线。
绘制模式
Draw Curve
通过绘制来修改曲线。
平滑曲线值
Smooth the curve values
用于平滑绘制的曲线。可多次点击,持续变平滑。
更新直方图
Calculate a more accurate histogram
点击此按钮,以计算更准确的直方图。
显示修剪
Show Clipping
当拖动黑滑块或白滑块时自动显示黑白场的修剪。
对于曲线调整图层,则须在“属性”面板控制菜单中设置。
曲线显示选项
Curves Display Options
曲线调整命令对话框的右侧列出了曲线显示选项。
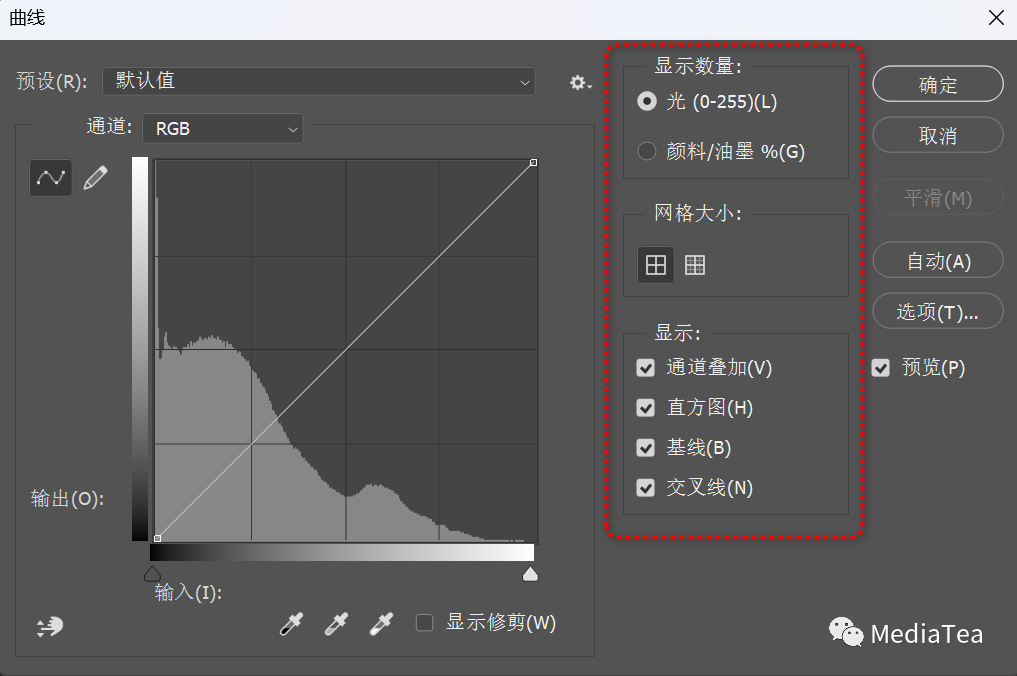
当使用曲线调整图层时,须从“属性”面板控制菜单中打开,如下图所示。
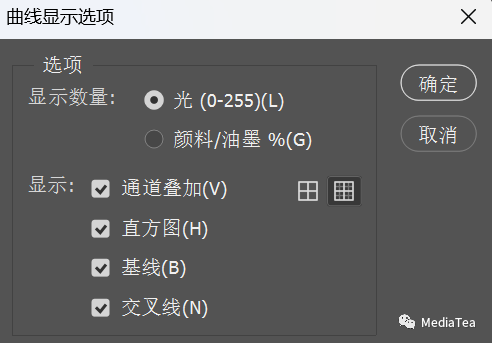
显示数量
Show Amount of
--光(0-255)
Light(0-255)
以显示光量的方式(加色)来显示曲线的坐标系。
--颜色/油墨
Pigment/Ink %
以显示颜料量的方式(减色)来显示曲线的坐标系。
显示:
Show:
网络大小
Grid Size
分别为 4 × 4 的简单网格和 10 × 10 的详细网格。
按住 Alt 键单击曲线框可进行切换。
通道叠加
Channel Overlays
在复合曲线上显示颜色通道。
直方图
Histogram
显示直方图作为参考。
基线
Baseline
显示基线(默认的对角线)。
交叉线
Intersection Line
显示用于确定点的精确位置的交叉线。

“点赞有美意,赞赏是鼓励”