一、整数规划简介
整数规划其实是线性规划和非线性规划的一个特殊情况,即有的变量取值只能是整数,不能是小数。这时候就需要一个新的函数来解决问题。
对于整数规划,分为线性整数规划和非线性整数规划
- 线性整数规划:MATLAB可进行求解(整数的意思:在线性规划的基础上,加入决策变量取整数的条件)
- 非线性整数规划:无特定算法,只用用近似算法,如蒙特卡罗模拟、启发式算法
整数中有一类比较特殊的0-1规划:特殊的整数规划,MATLAB中也只能求解线性0-1规划,对于非线性0-1规划也只能近似求解。
二、适用赛题
和前面线性规划和非线性规划的范围差不多。
三、模型流程
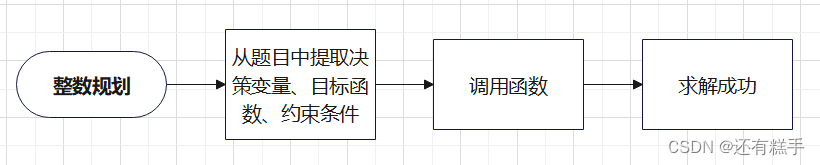
四、流程分析
1.提取信息
这一步和线性规划中的相同,不清楚请移步 数学建模【线性规划】 ,这里不再赘述。
2.调用函数
调用MATLAB自带的intlinprog函数。
[x, fval] = intlinprog(f, intcon, A, b, Aeq, beq, lb, ub)
| f | 目标函数的系数向量(必须是求最小值形式下的) |
| intcon | 指定哪些决策变量是整数 |
| A, b | 不等式约束条件的变量系数矩阵和常系数矩阵(必须是<或<=形式下的) |
| Aeq, beq | 等式约束条件的系数矩阵和常系数矩阵 |
| lb, ub | 决策变量的最小取值和最大取值 |
除了和linprog相同的注意事项,还有
- intlinprog不能指定初始值(新版本MATLAB可以在ub后加上初始值x0)
- 加入了intcon参数可以指定哪些决策变量是整数。例如:决策变量有三个:x1,x2,x3;若x1和x3是整数,则intcon = [1, 3]
对于线性整数0-1规划求解,仍然使用intlinprog函数,只不过在lb和ub上做文章。
例如:三个决策变量x1,x2,x3中,x1和x3是0-1变量,x2不限制,则intcon = [1, 3],lb = [0, -inf, 0]的转置,ub = [1, +inf, 1]的转置。
下面通过一个例子结束
目标函数:
min Z = -3x1 - 2x2 - x3
约束条件:
x1 + x2 + x3 ≤ 7
4x1 + 2x2 + x3 = 12
x1, x2 ≥ 0
x3 = 0或1
则代码为
f = [-3; -2; -1];
intcon = 3;
A = ones(1, 3);
b = 7;
Aeq = [4, 2, 1];
beq = 12;
lb = zeros(3, 1);
ub = [+inf; +inf; 1];
[x, fval] = intlinprog(f, intcon, A, b, Aeq, beq, lb, ub);求解成功。













![[ 云计算 | AWS ] ChatGPT 竞争对手 Claude 3 上线亚马逊云,实测表现超预期](https://img-blog.csdnimg.cn/direct/984008ea62d9400aa16e7cfe27c58a04.png)