2.组合总合III

• 题目描述

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9
• 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

• 题目分析

动态规划与回溯算法

刚读题目的大家可能会想到可以通过动态规划的0-1背包去解决这道题目，但是我们发现本题目的输出结果是集合的形式，如果用动态规划可能会导致存储结构复杂，所以我们可采用回溯算法去解决这道题目

回溯算法的思路

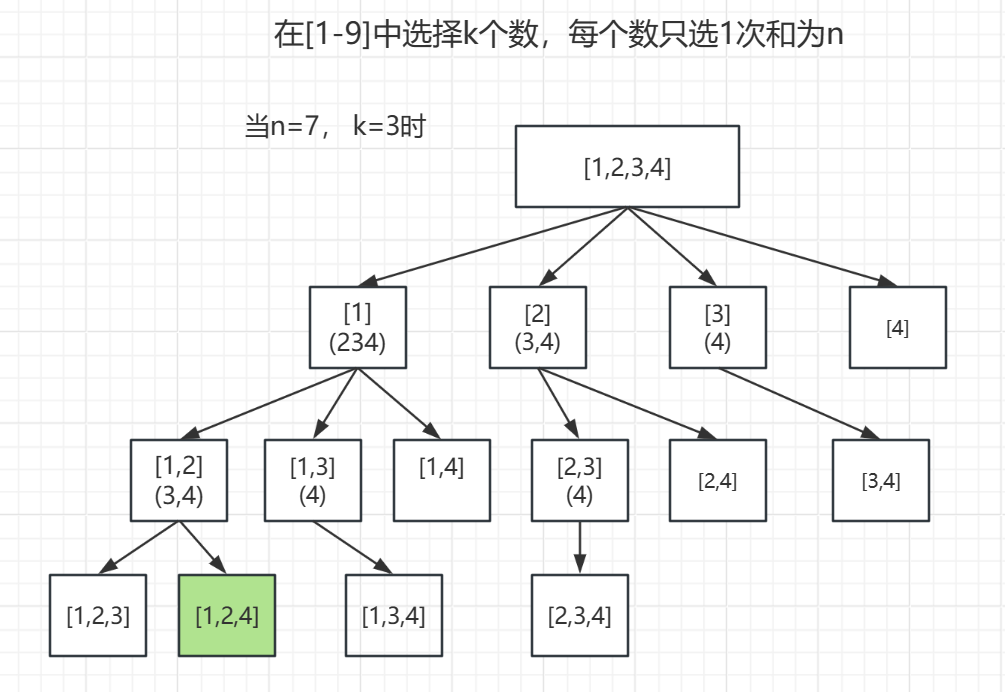
回溯算法是一种通过不断地尝试可能的解决方案来解决问题的方法。在解决问题时，我们尝试每一种可能的选择，当发现该选择并不符合要求时，则取消该选择，回溯到上一步，进行其他选择。
    
下面是该算法的题解步骤：

1.创建一个 LinkedList path 用于存储当前的组合路径，创建一个 List result 用于存储最终结果。

2.在 backtrack 方法中，首先判断是否满足终止条件，即当前路径的数字和等于 n 且路径长度为 k，如果满足则将当前路径加入结果集中；
在单层遍历逻辑中，从 startIndex 开始遍历到 9，这是因为剩余未遍历的数字数量要大于等于 k - path.size()。

3.在遍历过程中，依次将数字加入路径中，并更新当前数字和 sum；然后递归调用 backtrack 方法，继续向下搜索；搜索完成后进行回溯操作，将当前数字移出路径，恢复 sum 的值。

举例如下图

• Java代码实现

LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> result = new ArrayList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtrack(n, k, 1, 0);
        return result;
    }

    private void backtrack(int n, int k, int startIndex, int sum) {
        if (path.size() == k && sum == n) {
            result.add(new LinkedList<>(path));
            return;
        }

        for (int i = startIndex; i <= 9; i++) {
            if (sum >= n) return;
            sum += i;
            path.add(i);
            backtrack(n, k ,i + 1, sum);
            path.removeLast();
            sum -= i;
        }
    }

• 剪枝操作

为例提高代码运行的效率，我们可以进行一下剪枝操作：
1.当path的长度达到3时如果没有满足sum的条件则可以返回
2.当sum>t时说明已经超过要求解的范围，所以也可以直接返回
3.条件中要求满足path中要有k个数，但遍历的元素加上已有的path中的元素不足k时，则可以直接结束循环
path中的元素个数：path.size()
除了path中的元素还需要从i遍历到9剩余的元素个数：(9 - i + 1)
因此(9 - i + 1) + path.size() >= k
所以i要满足：10 + path.size() - k >= i
    
最终剪枝后的代码    
class Solution {
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> result = new LinkedList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
        backtrack(k, n, 1, 0);
        return result;
    }

    private void backtrack(int k, int n, int startIndex, int sum) {
        //终止条件
        if (n == sum && path.size() == k) {
            //收集结果
            result.add(new ArrayList<>(path));
            return;
        } else if (path.size() == k) {
            return;
        } else if (sum > n) {
            return;
        }

        //单层遍历的逻辑
        for (int i = startIndex; i <= 10 + path.size() - k; i++) {
            path.add(i);
            sum += i;
            backtrack(k, n, i + 1, sum);//递归
            sum -= i;//回溯
            path.removeLast();
        }
    }
}

• 代码中的小细节

为什么在result.add(new ArrayList<>(path));要new一个新的集合？

在代码中，new LinkedList<>(path)这行代码用于创建一个新的LinkedList对象，该对象包含与现有path列表相同的元素。这么做的原因是为了避免直接将path列表添加到result结果列表中，因为在回溯过程中path列表会不断地被修改，直接添加到result中可能会导致结果出错。因此，需要创建一个新的LinkedList对象来保存path的当前状态，以便在回溯过程中正确地记录和保存组合的情况。path是全局变量会变化的