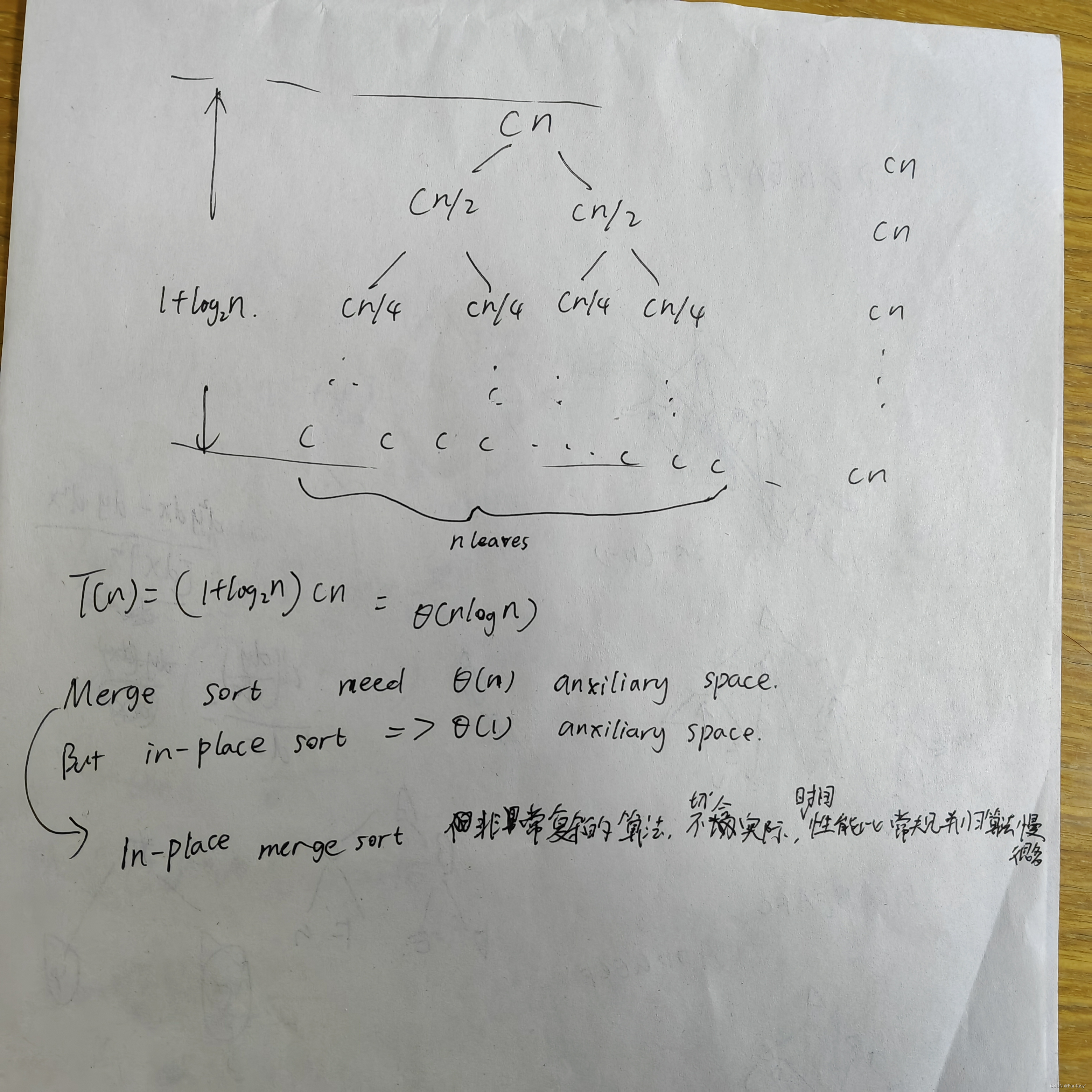
因为复习阶段全篇很细节的写下来一来比较费时间,二容易导致为了记笔记而记。
接下来的内容只会保留上课中比较有意义的地方,以及有自己助于理解的想法
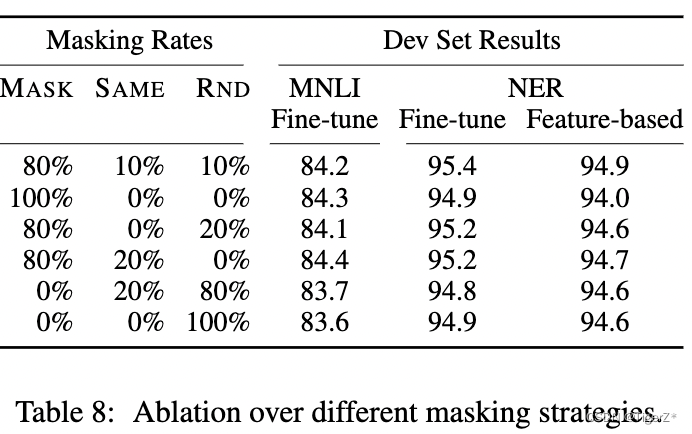
全微分


助记:
证明是否可微,首先判断两个偏导数是否存在,不存在则直接否定;
若存在,则接着利用可微的定义中(A为对x的偏导,B为对y的偏导,ρ为 )
代入后表示为高阶无穷小的形式(相除极限趋于0)即可证明

助记:
由两个一阶偏导连续一定能推出该函数在该点可微
对于证明中的最后两项,需要证明它们的和为ρ的高阶无穷小(同样利用除法证明)

但是可微不一定能推出两个偏导数都连续~
多元复合函数求导法则

助记:
找到该变量与求偏导对象的关系有哪些路径,分别按顺序求出后相加得到结果
尝试画出树形图,形式最复杂的在最顶上,最简单的变量位于叶子节点

用 f1、f2这样的符号表示对第一、二个参数位求导,形式更简洁


这里也可以改写为f1,f2,f3来简写
全微分形式不变性

右边为一元微分形式不变性

由于微分形式不变性,得到最终dx与dy前的系数应与展开后一致
而dx与dy原本的系数就是我们要求的结果,所以直接整理就能得到答案